强化学习—— 离散与连续动作空间(随机策略梯度与确定策略梯度)
1. 动作空间
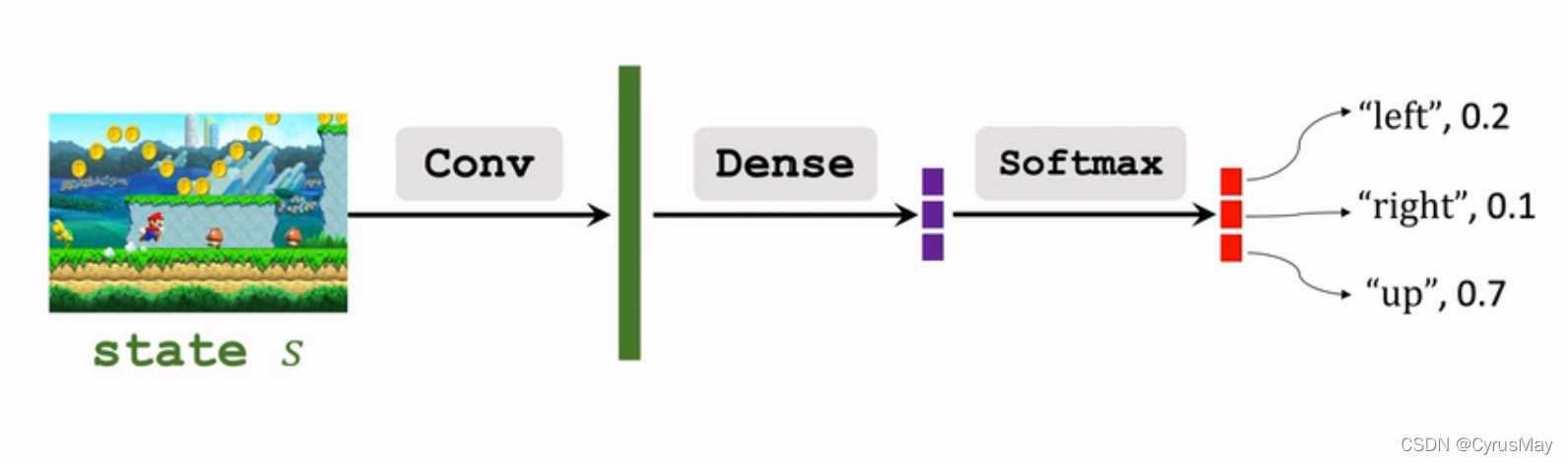
1.1 离散动作空间
- 比如: { l e f t , r i g h t , u p } \{left,right,up\} {left,right,up}
- DQN可以用于离散的动作空间(策略网络)
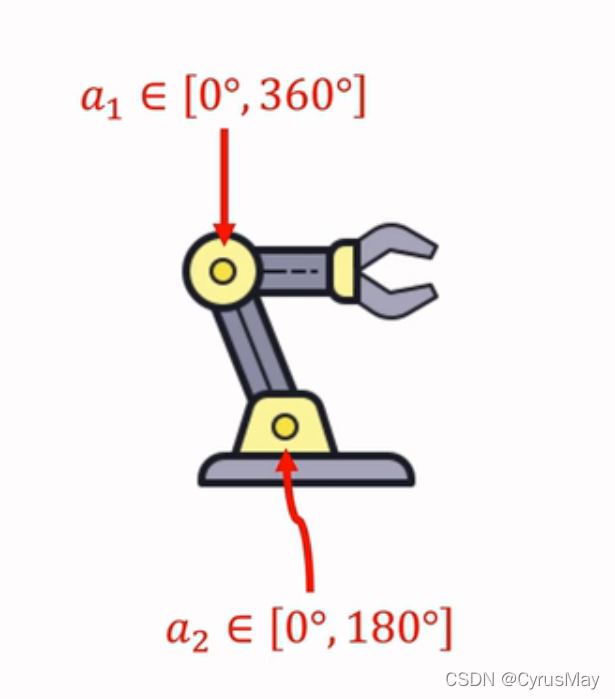
1.2 连续动作空间
- 比如:
A
=
[
0
°
,
18
0
°
]
?
[
0
°
,
36
0
°
]
A=[0^{\circ} ,180^{\circ} ]*[0^{\circ} ,360^{\circ} ]
A=[0°,180°]?[0°,360°]
- 连续动作空间的两种处理方式:
- 离散化(discretization):比如机械臂进行二维网格划分。假设d为连续动作空间的自由度,动作离散化后的数量会随着d的增加呈现指数增长,从而造成维度灾难。
- 使用确定策略梯度。
- 使用随机策略梯度。
2. 确定策略梯度做连续控制
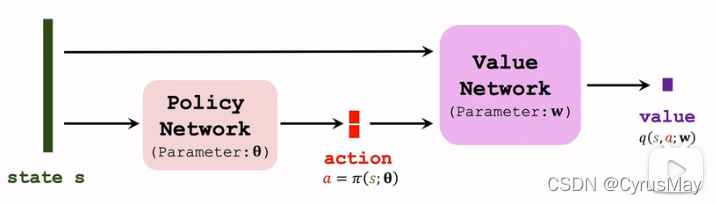
- 动作空间为 R d R^d Rd的一个子集
2.1 确定策略梯度推导
- 确定策略网络: a = π ( s ; θ ) a = \pi(s;\theta) a=π(s;θ)
- 价值网络(输出为一个标量):
q
(
s
,
a
;
W
)
q(s,a;W)
q(s,a;W)
网络学习过程为:
- 观测到一个transition: ( s t , a t , r t , s t + 1 ) (s_t,a_t,r_t,s_{t+1}) (st?,at?,rt?,st+1?)
- 计算t时刻价值网络的函数值: q t = q ( s t , a t ; W ) q_t = q(s_t,a_t;W) qt?=q(st?,at?;W)
- 计算t+1时刻价值网络的函数值: a t + 1 ? = π ( s t + 1 ; θ ) q t + 1 = q ( s t + 1 , a t + 1 ? ; W ) a_{t+1}^-=\pi(s_{t+1};\theta)\\q_{t+1}=q(s_{t+1},a_{t+1}^-;W) at+1??=π(st+1?;θ)qt+1?=q(st+1?,at+1??;W)
- TD Error为: δ t = q t ? ( r t + γ ? q t + 1 ) \delta_t=q_t-(r_t+\gamma\cdot q_{t+1}) δt?=qt??(rt?+γ?qt+1?)
- 更新价值网络: W ← W ? α ? ? q ( s t , a t ; W ) ? W W\gets W-\alpha\cdot\frac{\partial q(s_t,a_t;W)}{\partial W} W←W?α??W?q(st?,at?;W)?
- 更新策略网络所需的策略梯度推导: 策 略 网 络 的 目 标 为 通 过 策 略 网 络 a = π ( s ; θ ) 做 出 的 决 策 可 以 增 加 价 值 网 络 q = q ( s , a ; W ) 的 值 。 因 此 确 定 策 略 梯 度 ( d e t e r m i n i s t i c p o l i c y g r a d i e n t , D P G ) 为 : g = ? q ( s , π ( s ; θ ) ; W ) ? θ = ? q ( s . π ( s ; θ ) ; W ) ? π ( s ; θ ) ? ? π ( s ; θ ) ? θ 策略网络的目标为通过策略网络a=\pi(s;\theta)\\做出的决策可以增加价值网络q=q(s,a;W)的值。\\ 因此确定策略梯度(deterministic policy gradient, DPG)为:\\ g=\frac{\partial q(s,\pi(s;\theta);W)}{\partial \theta}=\frac{\partial q(s.\pi(s;\theta);W)}{\partial \pi(s;\theta)}\cdot \frac{\partial \pi(s;\theta)}{\partial \theta} 策略网络的目标为通过策略网络a=π(s;θ)做出的决策可以增加价值网络q=q(s,a;W)的值。因此确定策略梯度(deterministicpolicygradient,DPG)为:g=?θ?q(s,π(s;θ);W)?=?π(s;θ)?q(s.π(s;θ);W)???θ?π(s;θ)?
- 依据确定策略梯度进行策略网络参数更新: g = ? q ( s , π ( s ; θ ) ; W ) ? θ = ? q ( s . π ( s ; θ ) ; W ) ? π ( s ; θ ) ? ? π ( s ; θ ) ? θ θ ← θ + β ? g g=\frac{\partial q(s,\pi(s;\theta);W)}{\partial \theta}=\frac{\partial q(s.\pi(s;\theta);W)}{\partial \pi(s;\theta)}\cdot \frac{\partial \pi(s;\theta)}{\partial \theta}\\ \theta\gets \theta+\beta\cdot g g=?θ?q(s,π(s;θ);W)?=?π(s;θ)?q(s.π(s;θ);W)???θ?π(s;θ)?θ←θ+β?g
2.2 确定策略梯度网络的改进
2.2.1 使用Target网络
Bootstrapping现象:
- TD Target为: δ t = q t ? ( r t + γ ? q t ? 1 ) \delta_t =q_t-(r_t+\gamma\cdot q_{t-1}) δt?=qt??(rt?+γ?qt?1?)
- 价值网络使用到了自己的估计来更新自己,因而会造成连续高估或低估
- 解决方案为:使用不同的神经网络来进行TD Target计算
Target网络的核心思想:
- 使用价值网络计算 t t t时刻的价值函数值: q t = q ( s t , a t ; W ) q_t = q(s_t,a_t;W) qt?=q(st?,at?;W)
- 使用另外两个结构与价值网络和策略网络一致的神经网络计算t+1时刻的价值函数值和动作向量: a t + 1 ? = π ( s t + 1 ; θ ? ) q t + 1 = q ( s t + 1 , a t + 1 ? ; W ? ) a_{t+1}^-=\pi(s_{t+1};\theta^-)\\q_{t+1}=q(s_{t+1},a_{t+1}^-;W^-) at+1??=π(st+1?;θ?)qt+1?=q(st+1?,at+1??;W?)
采用Target网络的具体学习步骤为:
- 策略网络进行决策: a t = π ( s t ; θ ) a_t=\pi(s_t;\theta) at?=π(st?;θ)
- 采用确定策略梯度(DPG)更新策略网络: θ ← θ + β ? ? q ( s t , π ( s t ; θ ) ; W ) ? π ( s t ; θ ) ? ? π ( s t ; θ ) ? θ \theta\gets \theta+\beta\cdot \frac{\partial q(s_t,\pi(s_t;\theta);W)}{\partial \pi(s_t;\theta)}\cdot \frac{\partial \pi(s_t;\theta)}{\partial \theta} θ←θ+β??π(st?;θ)?q(st?,π(st?;θ);W)???θ?π(st?;θ)?
- 计算t时刻的价值网络函数值: q t = q ( s t , a t ; W ) q_t=q(s_t,a_t;W) qt?=q(st?,at?;W)
- 使用Target网络计算t+1时刻的价值: a t + 1 ? = π ( s t + 1 ; θ ? ) q t + 1 = q ( s t + 1 , a t + 1 ? ; W ? ) a_{t+1}^-=\pi(s_{t+1};\theta^-)\\q_{t+1}=q(s_{t+1},a_{t+1}^-;W^-) at+1??=π(st+1?;θ?)qt+1?=q(st+1?,at+1??;W?)
- 计算TD Error: δ t = q t ? ( r t + γ ? q t + 1 ) \delta_t=q_t-(r_t+\gamma \cdot q_{t+1}) δt?=qt??(rt?+γ?qt+1?)
- 更新价值网络的参数: W ← W ? α ? δ t ? ? q ( s t , a t ; W ) ? W W\gets W-\alpha\cdot \delta_t \cdot \frac{\partial q(s_t,a_t;W)}{\partial W} W←W?α?δt???W?q(st?,at?;W)?
Target 网络的参数更新步骤为:
- 设定超参数 τ ∈ [ 0 , 1 ] \tau \in [0,1] τ∈[0,1]
- 将价值网络、策略网络与Target网络的参数进行加权平均,从而实现参数更新: θ ? = τ ? θ + ( 1 ? τ ) ? θ ? W ? = τ ? W + ( 1 ? τ ) ? W ? \theta^- = \tau\cdot\theta+(1-\tau)\cdot \theta^-\\W^-=\tau\cdot W+(1-\tau)\cdot W^- θ?=τ?θ+(1?τ)?θ?W?=τ?W+(1?τ)?W?
2.2.2 其余改进
- 经验回放(experience replay)
- Multi-step TD Target
2.3 总结
| / | 随机策略网络 | 确定性策略网络 |
|---|---|---|
| 策略函数 | π ( a ∣ , s ; θ ) \pi(a|,s;\theta) π(a∣,s;θ) | a = π ( s ; θ ) a = \pi(s;\theta) a=π(s;θ) |
| 输出 | 动作空间的概率分布 | 确定的动作 a a a |
| 决策方式 | 根据动作空间的概率分布进行随机抽样 | 直接输出一个动作 a a a |
| 应用场景 | 多用于离散控制 | 连续控制 |
3. 随机策略网络进行连续控制
3.1 基本概念
- 折扣回报: U t = R t + γ ? R t + 1 + γ 2 ? R t + 2 + . . . U_t = R_t+\gamma\cdot R_{t+1}+\gamma^2\cdot R_{t+2}+... Ut?=Rt?+γ?Rt+1?+γ2?Rt+2?+...
- 动作价值函数: Q π ( s t , a t ) = E [ U t ∣ S t = s t , A t = a t ] Q_\pi(s_t,a_t)=E[U_t|S_t=s_t,A_t=a_t] Qπ?(st?,at?)=E[Ut?∣St?=st?,At?=at?]
- 状态价值函数: V π ( s t ) = E A t [ Q π ( s t , A t ) ] V_\pi(s_t)=E_{A_t}[Q_\pi(s_t,A_t)] Vπ?(st?)=EAt??[Qπ?(st?,At?)]
- 策略梯度: ? V π ( s t ) ? θ = E A t ~ π [ Q π ( s t , A t ) ? ? l o g ( π ( A t ∣ s t ; θ ) ) ? θ ] g ( A t ) = Q π ( s t , A t ) ? ? l o g ( π ( A t ∣ s t ; θ ) ) ? θ \frac{\partial V_\pi(s_t)}{\partial \theta}=E_{A_t\sim \pi}[Q_\pi(s_t,A_t)\cdot\frac{\partial log(\pi(A_t|s_t;\theta))}{\partial \theta}]\\g(A_t)=Q_\pi(s_t,A_t)\cdot\frac{\partial log(\pi(A_t|s_t;\theta))}{\partial \theta} ?θ?Vπ?(st?)?=EAt?~π?[Qπ?(st?,At?)??θ?log(π(At?∣st?;θ))?]g(At?)=Qπ?(st?,At?)??θ?log(π(At?∣st?;θ))?
- 进行蒙特卡洛近似后的策略梯度为: a t ~ π ( ? ∣ s t ; θ ) g ( a t ) = Q π ( s t , a t ) ? ? l o g ( π ( a t ∣ s t ; θ ) ) ? θ a_t\sim\pi(\cdot|s_t;\theta)\\g(a_t)=Q_\pi(s_t,a_t)\cdot\frac{\partial log(\pi(a_t|s_t;\theta))}{\partial \theta} at?~π(?∣st?;θ)g(at?)=Qπ?(st?,at?)??θ?log(π(at?∣st?;θ))?
3.2 策略网络
3.2.1 自由度为1的连续动作空间
- 假设 μ \mu μ和 σ \sigma σ为状态 s s s的函数
- 假设策略函数为正态分布的概率密度函数: π ( a ∣ s ) = 1 2 π ? σ e ? ( a ? μ ) 2 2 σ 2 \pi(a|s)=\frac{1}{\sqrt{2\pi}\cdot\sigma}e^{-\frac{(a-\mu)^2}{2\sigma^2}} π(a∣s)=2π??σ1?e?2σ2(a?μ)2?
3.2.2 自由度大于1(为 d d d)的连续动作空间
- 动作空间为d维向量
- μ \mu μ和 σ \sigma σ为状态 s s s的函数: s → R d s\to R^d s→Rd
- μ i \mu_i μi?和 σ i \sigma_i σi?为 μ ( s ) \mu(s) μ(s)和 σ ( s ) \sigma(s) σ(s)的第 i i i个元素
- 则定义策略函数为: π ( a ∣ s ) = Π i = 1 d 1 2 π ? σ i e ? ( a ? μ i ) 2 2 σ i 2 \pi(a|s)=\Pi_{i=1}^d \frac{1}{\sqrt{2\pi}\cdot\sigma_i}e^{-\frac{(a-\mu_i)^2}{2\sigma_i^2}} π(a∣s)=Πi=1d?2π??σi?1?e?2σi2?(a?μi?)2?
3.2.3 函数近似
- 对均值的近似: μ ( s ) ← μ ( s ; θ μ ) \mu(s)\gets \mu(s;\theta^\mu) μ(s)←μ(s;θμ)
- 对方差的对数进行近似: ρ i = l o g ( σ i 2 ) i = 1 , 2 , . . . , d ρ ← ρ ( s ; θ ρ ) \rho_i = log(\sigma_i^2) \quad i = 1,2,...,d\\\rho\gets \rho(s;\theta^\rho) ρi?=log(σi2?)i=1,2,...,dρ←ρ(s;θρ)
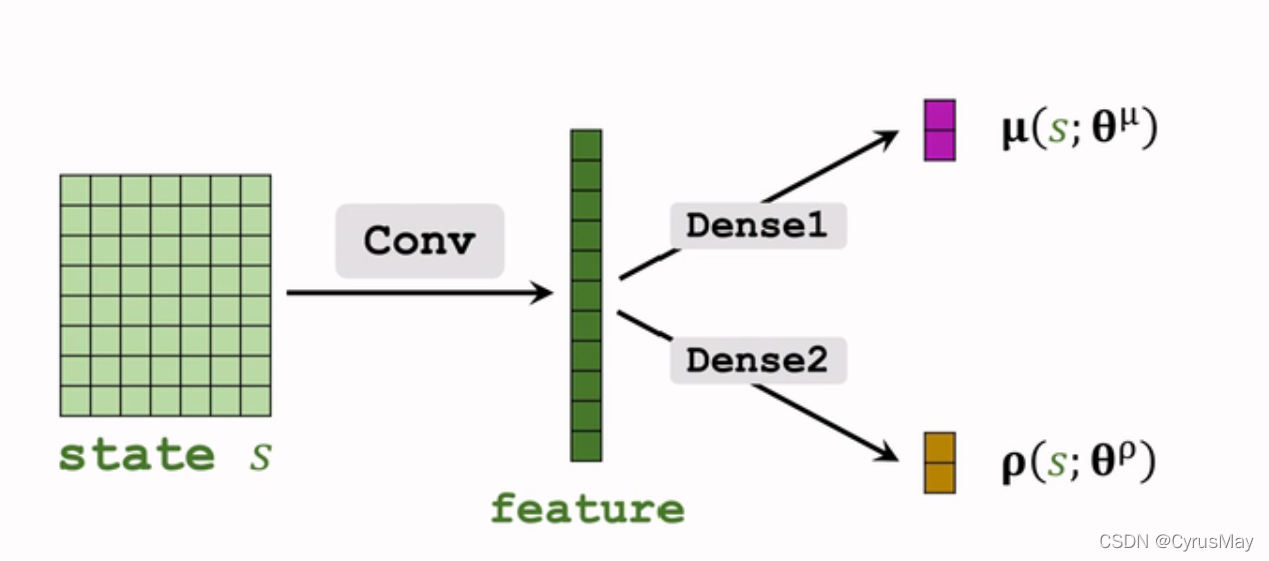
3.2.4 连续控制策略
- 观测到状态 s t s_t st?
- 通过神经网络计算均值和方差: μ ^ = μ ( s t ; θ ) ρ ^ = ρ ( s t ; θ ) σ i ^ 2 = e ρ i i = 1 , 2 , . . . , d \hat{\mu}=\mu(s_t;\theta)\\\hat{\rho}=\rho(s_t;\theta)\\\hat{\sigma_i}^2=e^{\rho_i} \quad i = 1,2,...,d μ^?=μ(st?;θ)ρ^?=ρ(st?;θ)σi?^?2=eρi?i=1,2,...,d
- 进行随机抽样得到动作 a a a: a i ~ N ( u i ^ , σ i ^ 2 ) i = 1 , 2 , . . . , d a_i\sim N(\hat{u_i},\hat{\sigma_i}^2)\quad i = 1,2,...,d ai?~N(ui?^?,σi?^?2)i=1,2,...,d
3.2.5 添加辅助神经网络
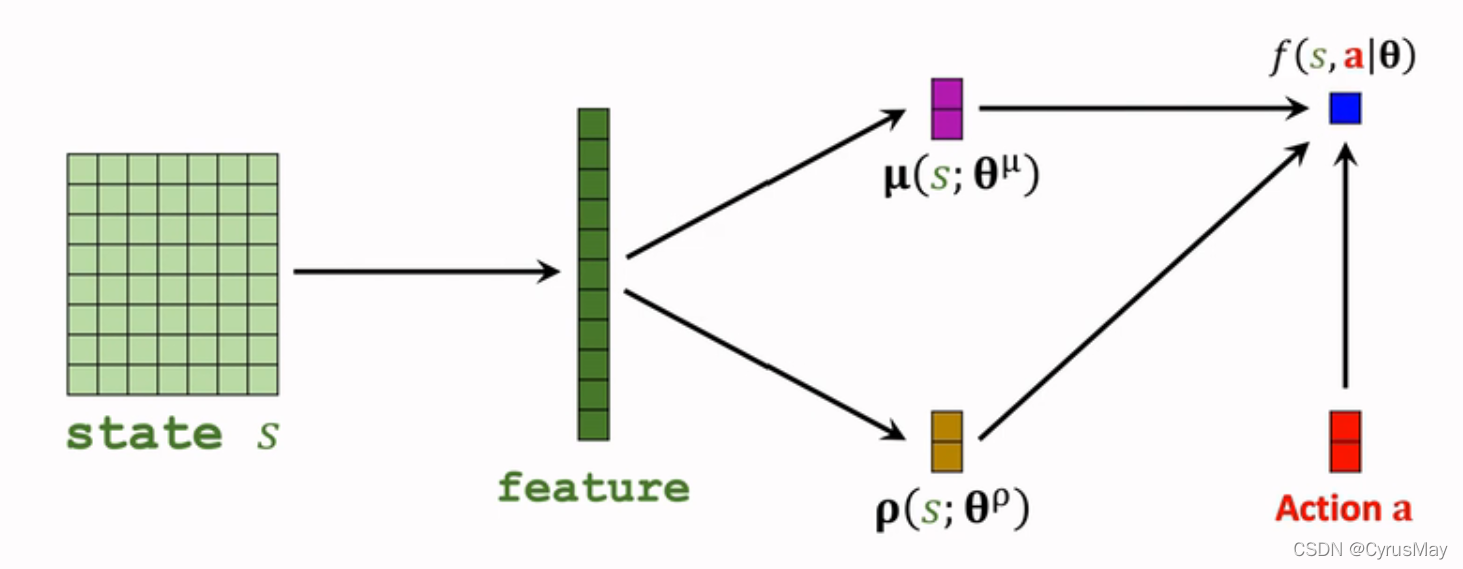
- 策略网络为: π ( a ∣ s ; θ μ , θ ρ ) = Π i = 1 d 1 2 π ? σ i ? e ? ( a ? μ i ) 2 2 σ i 2 l o g ( π ( a ∣ s ; θ μ , θ ρ ) ) = ∑ i = 1 d [ ? l o g ( σ i ) ? ( a ? μ i ) 2 2 σ i 2 ] + c o n s t l o g ( π ( a ∣ s ; θ μ , θ ρ ) ) = ∑ i = 1 d [ ? ρ i 2 ? ( a ? μ i ) 2 2 ? e ρ i ] + c o n s t log ? ( π ( a ∣ s ; θ μ , θ ρ ) ) = f ( s , a ; θ ) θ = ( θ μ , θ ρ ) \pi(a|s;\theta^\mu,\theta^\rho)=\Pi_{i=1}^d\frac{1}{\sqrt{2\pi}\cdot\sigma_i}\cdot e^{-\frac{(a-\mu_i)^2}{2\sigma_i^2}} \\ log(\pi(a|s;\theta^\mu,\theta^\rho))=\sum_{i=1}^d[-log(\sigma_i)-\frac{(a-\mu_i)^2}{2\sigma_i^2}]+const\\log(\pi(a|s;\theta^\mu,\theta^\rho))=\sum_{i=1}^d[-\frac{\rho_i}{2}-\frac{(a-\mu_i)^2}{2\cdot e^{\rho_i}}]+const\\\log(\pi(a|s;\theta^\mu,\theta^\rho))=f(s,a;\theta)\quad \theta=(\theta^\mu,\theta^\rho) π(a∣s;θμ,θρ)=Πi=1d?2π??σi?1??e?2σi2?(a?μi?)2?log(π(a∣s;θμ,θρ))=i=1∑d?[?log(σi?)?2σi2?(a?μi?)2?]+constlog(π(a∣s;θμ,θρ))=i=1∑d?[?2ρi???2?eρi?(a?μi?)2?]+constlog(π(a∣s;θμ,θρ))=f(s,a;θ)θ=(θμ,θρ)
- 定义上述的 f ( s , a ; θ ) f(s,a;\theta) f(s,a;θ)为辅助神经网络,则得到三个神经网络: μ ( s ; θ μ ) 正 态 分 布 的 均 值 ρ ( s ; θ ρ ) 正 态 分 布 的 对 数 方 差 f ( s , a ; θ ) 辅 助 神 经 网 络 用 于 训 练 策 略 神 经 网 络 \mu(s;\theta^\mu)\quad 正态分布的均值\\\rho(s;\theta^\rho)\quad正态分布的对数方差\\f(s,a;\theta)\quad 辅助神经网络用于训练策略神经网络 μ(s;θμ)正态分布的均值ρ(s;θρ)正态分布的对数方差f(s,a;θ)辅助神经网络用于训练策略神经网络
- 随机策略梯度为: g ( a ) = ? l o g ( π ( a ∣ s ; θ ) ) ? θ ? Q π ( s , a ) f ( s , a ; θ ) = l o g ( π ( a ∣ s ; θ ) ) + c o n s t g ( a ) = ? f ( s , a ; θ ) ? θ ? Q π ( s , a ) g(a )= \frac{\partial log(\pi(a|s;\theta))}{\partial \theta}\cdot Q_\pi(s,a)\\ f(s,a;\theta)=log(\pi(a|s;\theta))+const\\g(a )=\frac{\partial f(s,a;\theta)}{\partial \theta}\cdot Q_\pi(s,a) g(a)=?θ?log(π(a∣s;θ))??Qπ?(s,a)f(s,a;θ)=log(π(a∣s;θ))+constg(a)=?θ?f(s,a;θ)??Qπ?(s,a)
3.2.6 状态价值函数的近似
- 使用reinforce算法: u t = r t + γ ? r t + 1 + . . . θ ← θ + β ? ? f ( s , a ; θ ) ? θ ? u t u_t = r_t+\gamma\cdot r_{t+1}+...\\\theta\gets\theta+\beta\cdot\frac{\partial f(s,a;\theta)}{\partial \theta}\cdot u_t ut?=rt?+γ?rt+1?+...θ←θ+β??θ?f(s,a;θ)??ut?
- 使用 A-C算法: Q π ~ q ( s , a ; W ) θ ← θ + β ? ? f ( s , a ; θ ) ? θ ? q ( s , a ; W ) Q_\pi\sim q(s,a;W)\\\theta\gets\theta+\beta\cdot\frac{\partial f(s,a;\theta)}{\partial \theta}\cdot q(s,a;W) Qπ?~q(s,a;W)θ←θ+β??θ?f(s,a;θ)??q(s,a;W)
4 总结
- 连续动作空间有无穷多种动作数量
- 解决方案包括:
- 离散动作空间,使用标准DQN或者策略网络进行学习,但是容易引起维度灾难
- 使用确定策略网络进行学习(但没有随机性)
- 随即策略网络( μ 与 σ 2 \mu与\sigma^2 μ与σ2)
- 训练过程的技巧:
- 构造辅助神经网络 f ( s , a ; θ ) f(s,a;\theta) f(s,a;θ)计算策略梯度
- 策略梯度近似算法包括:reinforce、Actor-Critic算法
- 可以改进reinforce算法,使用带有baseline的reinforce算法
- 可以改进Actor-Critic算法,使用A2C算法
本文内容为参考B站学习视频书写的笔记!
时间是贼
偷走一切
————五月天(如烟)————
by CyrusMay 2022 04 13
