Pytorch之nn.Conv1d学习个人见解

一、官方文档（务必先耐心阅读）

官方文档：点击打开《CONV1D》

二、Conv1d个人见解

Conv1d类构成

class torch.nn.Conv1d(in_channels, out_channels, kernel_size,stride=1, padding=0, dilation=1, groups=1, bias=True)
in_channels(int)—输入数据的通道数。在文本分类中，即为句子中单个词的词向量的维度。 （word_vector_num）
out_channels(int)—输出数据的通道数。设置 N 个输出通道数，就有 N 个1维卷积核。（new word_vector_num）
kernel_size(int or tuple) —卷积核的长度，1维卷积中卷积核的实际大小维度是（in_channels，kernel_size），顺序不可互换。
stride(int or tuple, optional)—卷积步长。
padding (int or tuple, optional)—输入的每一条边补充0的层数。
dilation(int or tuple, `optional``)—卷积核元素之间的间距。
groups(int, optional)—从输入通道到输出通道的阻塞连接数。
bias(bool, optional)—如果bias=True，添加偏置。

具体案例分析

原始数据集说明：6批句子（batch_size），每批句子5个单词（sentence_word_num），每个单词的词向量为3维通道（word_vector_num），数据集的维度表示为 [6,5,3] 。
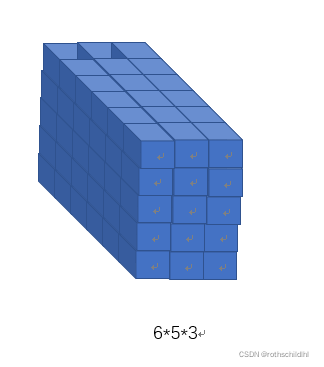
模型输入数据集说明：在上步原始数据集中进行维度转换，6批句子（batch_size），每个单词的词向量为3维通道（word_vector_num），每批句子5个单词（sentence_word_num），数据集的维度表示为 [6,3,5] 。（注意：为什么需要维度转换呢？因为Conv1d模型的卷积核大小是[输入通道数，卷积核的长]，那么数据集和卷积核的内积运算必须维度都一致）
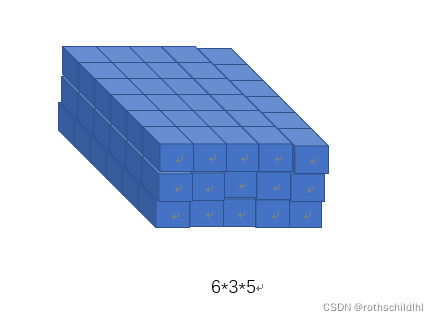
Conv1d模型参数说明：输入通道数设定为3（数量等同 word_vector_num ），输出通道数设定为8（数量表示new word_vector_num），卷积核的长设定为2。
Conv1d模型权重参数（W）维度则根据上步自动生成为 [8,3,2] ,表示 [输出通道数,输入通道数,卷积核的长]，又因为卷积核等同表示 [输入通道数,卷积核的长]，输出通道数等同表示卷积核的个数，则总而言之，此模型权重参数的维度表示：有8个大小为[3,2]的卷积核去对输入数据做卷积运算。
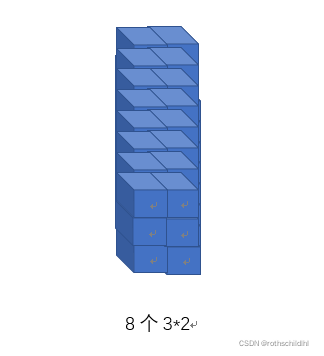
卷积过程中的数据计算说明（非常重要）：模型输入数据是一个深度为6长为3宽为5的三维数据，卷积核长为3宽度为2的二维数据，步长默认为1进行移动。先考虑深度为1的情况（可以先暂时不考虑深度这一维进行理解），模型输入数据变成一个长为3宽为5的二维数据，每个卷积核每次完成一次移动后，实现模型输入数据的6个数和这个卷积核的6个数（3*2）进行内积再和，生成1个数。每个卷积核总共需要横向移动四次（见下图动画理解），那么每个卷积核完成卷积后生成数据维度是[1,4]，那么8个卷积核完成卷积生成的数据维度是[8,4]，若要加上深度这一维就是[1,8,4]。再考虑深度为6的情况，进行卷积后得到的数据是深度为1的情况下的6倍，也就是[6,8,4]。
模型输出数据集说明：6批句子（batch_size），每个单词的词向量为8维通道（new word_vector_num），每批句子4个单词（new sentence_word_num），数据集的维度表示为 [6,8,4] 。
源代码如下：

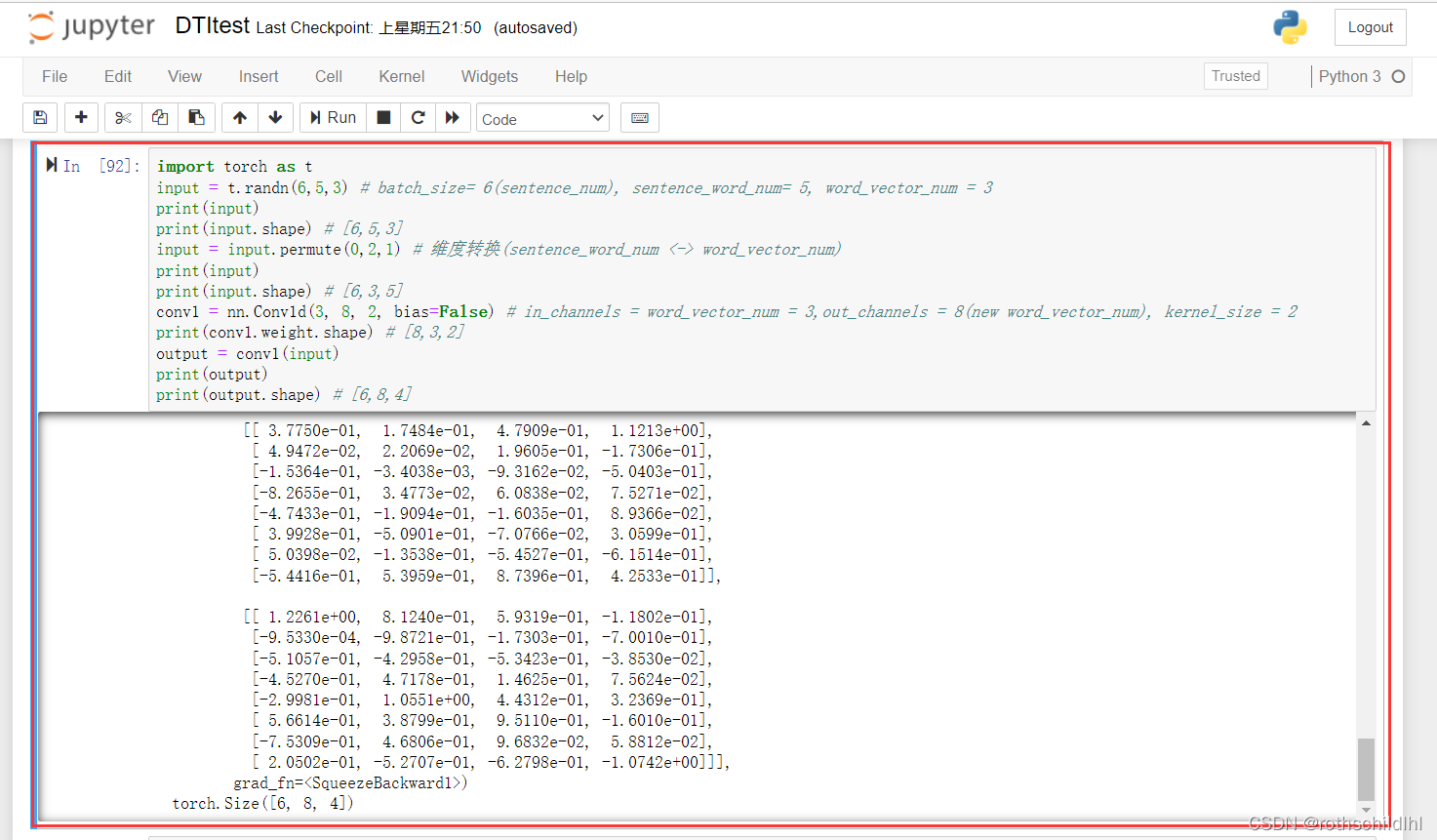
import torch as t
input = t.randn(6,5,3) # batch_size= 6(sentence_num), sentence_word_num= 5, word_vector_num = 3
print(input)
print(input.shape) # [6,5,3]
input = input.permute(0,2,1) # 维度转换(sentence_word_num <-> word_vector_num) 
print(input)
print(input.shape) # [6,3,5]
conv1 = nn.Conv1d(3, 8, 2, bias=False) # in_channels = word_vector_num = 3,out_channels = 8(new word_vector_num), kernel_size = 2
print(conv1.weight.shape) # [8,3,2]
output = conv1(input)
print(output)
print(output.shape) # [6,8,4]

代码运行结果如下：

tensor([[[-1.5697,  1.6189,  0.4521],
         [-0.9188, -0.5753,  1.4038],
         [ 1.0623,  0.6014, -0.7945],
         [-1.0525,  2.0641, -1.8544],
         [-1.0642, -0.2318,  0.1935]],

        [[-2.2800, -1.1117, -1.0796],
         [ 0.2286,  0.6835, -2.6689],
         [-0.5956,  0.7648,  2.7674],
         [-0.9383,  0.2043,  1.3341],
         [-1.0337, -1.4724, -0.9340]],

        [[-0.9657,  0.2571,  0.6817],
         [ 0.3036, -1.0275, -0.0496],
         [ 1.5626,  0.5038, -0.3329],
         [-0.1654,  1.8341,  0.1949],
         [-0.1841, -0.1558, -0.1641]],

        [[-0.2144, -1.3156,  0.8448],
         [-0.5384,  1.2287,  1.5028],
         [ 0.2343, -1.0956, -0.5923],
         [ 0.2661,  1.1084,  0.4200],
         [-2.7000, -1.0146,  0.2574]],

        [[-0.2548, -1.6011, -0.8730],
         [ 0.1237, -0.2313,  0.8306],
         [ 0.9188,  0.5165,  0.8517],
         [ 0.0083, -0.4545,  0.9021],
         [-0.8566, -0.9456,  1.4411]],

        [[ 0.0890, -0.9539,  0.1321],
         [-0.8780, -1.2702,  1.9250],
         [-0.4996, -0.4644, -0.8101],
         [-2.2298, -0.8780, -0.1641],
         [ 0.1206,  0.0420, -0.0975]]])
torch.Size([6, 5, 3])
tensor([[[-1.5697, -0.9188,  1.0623, -1.0525, -1.0642],
         [ 1.6189, -0.5753,  0.6014,  2.0641, -0.2318],
         [ 0.4521,  1.4038, -0.7945, -1.8544,  0.1935]],

        [[-2.2800,  0.2286, -0.5956, -0.9383, -1.0337],
         [-1.1117,  0.6835,  0.7648,  0.2043, -1.4724],
         [-1.0796, -2.6689,  2.7674,  1.3341, -0.9340]],

        [[-0.9657,  0.3036,  1.5626, -0.1654, -0.1841],
         [ 0.2571, -1.0275,  0.5038,  1.8341, -0.1558],
         [ 0.6817, -0.0496, -0.3329,  0.1949, -0.1641]],

        [[-0.2144, -0.5384,  0.2343,  0.2661, -2.7000],
         [-1.3156,  1.2287, -1.0956,  1.1084, -1.0146],
         [ 0.8448,  1.5028, -0.5923,  0.4200,  0.2574]],

        [[-0.2548,  0.1237,  0.9188,  0.0083, -0.8566],
         [-1.6011, -0.2313,  0.5165, -0.4545, -0.9456],
         [-0.8730,  0.8306,  0.8517,  0.9021,  1.4411]],

        [[ 0.0890, -0.8780, -0.4996, -2.2298,  0.1206],
         [-0.9539, -1.2702, -0.4644, -0.8780,  0.0420],
         [ 0.1321,  1.9250, -0.8101, -0.1641, -0.0975]]])
torch.Size([6, 3, 5])
torch.Size([8, 3, 2])
tensor([[[ 1.8743e-01, -1.4395e-01, -6.9980e-01, -8.2561e-01],
         [-2.7898e-01, -6.5680e-01,  5.2309e-01,  3.0150e-01],
         [-1.7926e-01,  1.0438e-01, -1.4334e-01,  2.2036e-01],
         [ 9.1778e-01,  3.4689e-01,  8.8961e-01,  4.0392e-01],
         [ 2.5770e-01,  5.3539e-01,  5.1576e-01, -1.7502e-01],
         [-5.9272e-01, -4.6085e-01,  1.0932e-02, -2.7211e-01],
         [-1.2418e+00,  4.5105e-01,  1.5149e+00, -7.5503e-01],
         [ 4.5389e-01, -3.1628e-01,  2.4424e-01, -1.5187e-01]],

        [[-1.0650e+00, -1.6615e-01,  1.0677e+00,  4.9309e-01],
         [-8.1073e-01,  1.1998e+00, -5.1610e-01, -8.7283e-01],
         [ 2.9464e-01, -1.3378e-01, -6.7559e-01, -1.9098e-01],
         [ 5.6014e-04, -3.3817e-01,  1.5722e+00,  5.0429e-01],
         [ 7.1028e-01, -1.3099e+00,  9.0939e-01,  9.6488e-01],
         [ 1.6606e-01, -3.9754e-01, -6.4322e-01,  4.8480e-01],
         [ 1.2543e+00, -7.9167e-01, -5.4348e-01, -2.5640e-01],
         [-2.1250e+00,  7.5991e-01,  1.2818e+00, -5.1833e-01]],

        [[ 4.8963e-02, -3.0574e-01, -2.1625e-01, -4.4589e-01],
         [-5.3250e-01,  3.3740e-02,  8.2394e-01,  4.8748e-02],
         [ 1.6242e-01,  3.1454e-01, -1.5465e-01,  2.2231e-01],
         [-1.6153e-02, -6.8735e-01,  4.7351e-01,  5.9774e-01],
         [ 2.0333e-01, -3.8176e-01, -2.0578e-01,  1.5212e-01],
         [-6.1877e-02, -1.3378e-01, -3.8114e-01, -4.3941e-01],
         [-5.9499e-01,  4.4317e-01,  6.7399e-01, -5.4335e-01],
         [-3.5491e-01, -2.9921e-01,  1.0920e+00,  4.3913e-01]],

        [[ 9.3993e-01, -4.9535e-02,  3.9259e-02,  8.4282e-01],
         [-3.1526e-02, -5.7992e-01,  2.8747e-01, -3.4273e-02],
         [-7.4271e-01,  2.4287e-01, -1.6298e-01, -6.4197e-01],
         [ 5.4584e-01,  4.5684e-01, -2.3048e-01,  9.3792e-01],
         [ 2.0335e-01,  5.2475e-01, -2.9436e-01,  7.0134e-01],
         [-2.3952e-01, -2.1741e-01, -6.2856e-02,  6.1455e-01],
         [ 3.9216e-01, -6.6250e-01,  5.9392e-01, -4.2417e-01],
         [ 5.9883e-01,  7.8288e-02,  6.9463e-04,  5.3361e-01]],

        [[ 3.7750e-01,  1.7484e-01,  4.7909e-01,  1.1213e+00],
         [ 4.9472e-02,  2.2069e-02,  1.9605e-01, -1.7306e-01],
         [-1.5364e-01, -3.4038e-03, -9.3162e-02, -5.0403e-01],
         [-8.2655e-01,  3.4773e-02,  6.0838e-02,  7.5271e-02],
         [-4.7433e-01, -1.9094e-01, -1.6035e-01,  8.9366e-02],
         [ 3.9928e-01, -5.0901e-01, -7.0766e-02,  3.0599e-01],
         [ 5.0398e-02, -1.3538e-01, -5.4527e-01, -6.1514e-01],
         [-5.4416e-01,  5.3959e-01,  8.7396e-01,  4.2533e-01]],

        [[ 1.2261e+00,  8.1240e-01,  5.9319e-01, -1.1802e-01],
         [-9.5330e-04, -9.8721e-01, -1.7303e-01, -7.0010e-01],
         [-5.1057e-01, -4.2958e-01, -5.3423e-01, -3.8530e-02],
         [-4.5270e-01,  4.7178e-01,  1.4625e-01,  7.5624e-02],
         [-2.9981e-01,  1.0551e+00,  4.4312e-01,  3.2369e-01],
         [ 5.6614e-01,  3.8799e-01,  9.5110e-01, -1.6010e-01],
         [-7.5309e-01,  4.6806e-01,  9.6832e-02,  5.8812e-02],
         [ 2.0502e-01, -5.2707e-01, -6.2798e-01, -1.0742e+00]]],
       grad_fn=<SqueezeBackward1>)
torch.Size([6, 8, 4])

在这里插入图片描述

三、Conv1d和Conv2d的联系和区别

两者关于批次的理解是一样的：也就是按照有多少组数据进行理解，比如上面的案例是6批数据，也就是6组数据。
输入通道数理解不同：Conv1d的通道数是指词向量的维度，Conv2d的通道数是指颜色通道比如：黑白图的通道数是1和RGB彩色图的通道数为3或者设置更多的颜色通道数。
卷积核大小不同：Conv1d的卷积核是[输入通道数，卷积核的长]，Conv2d的卷积核是[输入通道数，卷积核的长，卷积核的宽]。
卷积核移动路线不同：Conv1d的卷积核只能横向移动，Conv2d的卷积核可以横向纵向移动。
输出通道数理解相同，都是指卷积核的个数，也是新的输入通道数。
对比理解可参考一个Conv2d案例：点击打开《图像相关层之卷积锐化图片示例》文章