1. 对梯度的理解
借用百度上对梯度的定义:梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
简单来说:梯度就是一个函数最陡的方向。

更多关于梯度、偏导数、方向导数可参考:链接
2.对梯度下降的理解
借用吴恩达老师的话,把下降比作下山,那么梯度下降就是找一个方向,沿着该方向能最快下山。

3. 模拟梯度下降过程
说明:代码编写和测试均在notebook中实现
3.1 绘制测试函数
先绘制出测试用的函数y=(x-2.5)^2 - 1:

3.2 模拟梯度下降的过程
epsilon = 1e-8 # 误差
alpha = 0.1 # 学习率
# 函数的定义
def J(theta):
return (theta - 2.5)**2 - 1.
# 导数的定义
def dJ(theta):
return 2*(theta - 2.5)
# 梯度下降(这里说梯度下降不太准确,因为这里用的是一元函数的导数)
theta = 0.0
while True:
gradient = dJ(theta) # 计算导数
last_theta = theta # 记录上一个自变量
theta = theta - alpha * gradient # 更新自变量
if (abs(J(theta) - J(last_theta)) < epsilon): # 当两个函数值之差小于误差时就停止下降
break
print(theta)
print(J(theta))
最终得到的theta值和其对应的函数值如下:
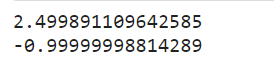
基本接近函数的最小点和最小值。
3.3 下降过程
将这一过程绘制出来,直观的看一下下降的过程:

可以看到,从我们设置的初始值0开始,逐渐沿着函数下降的方向走,而且走的步子越来越小。
这也对应了吴恩达老师讲的:“当我们接近局部最低点时,梯度下降法会自动采取更小的幅度”。当接近局部最低点时,导数值接近0,也就是说,接近局部最低点时导数值也相应的会变小,“所以梯度下降将自动采取较小的幅度,这就是梯度下降的做法。所以实际上没有必要再另外减小𝑎。”
3.4 不同alpha对下降的影响
上文说到alpha的大小决定了每次下降的步长,也就是每次下山要迈多大的步子,那就采用不同的alpha值测试一下,看看不同alpha值对应的下降过程是怎样的。
(1)alpha = 0.01

我们之前看到了alpha=0.1时的情况,当alpha变为0.01时可以明显的看到每次的步长变得更小,而且走的步数也多了。
(2)alpha = 0.8

当alpha变为0.8时,下降情况就和之前有所不同了,有些像摇摆的方式往下走,但是最后也收敛了。
(3)alpha = 1.1

从图中可以看到当alpha取值过大时,最后会导致不收敛,不往最低点走了,反而往外跑了。
从测试结果来看,学习率alpha的选择对梯度下降是很重要的,若alpha太小,会导致收敛速度太慢;若alpha太大,会导致结果不收敛甚至发散。
3.5 初始值的选取
我们在3.4看到了不同的学习率值对下降过程的影响,那初始值对下降过程是否有影响呢?答案是肯定的。
在之前的测试中,我们选择的初始值都是0, 0在函数y = (x - 2.5)^2 - 1最低点的附近,但是如果一开始就将初始值选在函数的最低点会怎样?
选取初始值为2.5,下降过程为:

可以看到小红点就没动,一直待在最低点。因为我们一开始就将初始值放在了(局部)最低点,此处的导数值为0,那么在这一步更新时,theta的值不会变:
theta = theta - alpha * gradient # 更新自变量
也就是说此时梯度下降根本没有更新theta的值,也就是开始即结束,此处再引用吴恩达老师的话:“这也解释了为什么即使
学习速率𝑎保持不变时,梯度下降也可以收敛到局部最低点”
4. 线性回归中的梯度下降
4.1 准备工作
假设样本数据和线性函数为:

说明:可能有人看的是吴恩达老师的课程,吴恩达老师的课程中样本数据设置的是列向量,即列方向是样本的特征,行方向是样本个数,和这里有所不同。本文中行方向是样本特征,列方向是样本个数。
我们的目标就是寻找参数theta,使得损失函数最小:

那么在更新theta时就是:

4.2 代码实现
# theta为参数,X_b为增添了X0列之后的自变量
def J(theta, X_b, y):
try:
return np.sum((y - X_b.dot(theta)) ** 2) / (2 * len(X_b)) # 损失函数J
except:
return float('inf')
def dJ(theta, X_b, y):
res = np.empty(len(theta))
res[0] = np.sum(X_b.dot(theta) - y) # X0恒为1
for i in range(1, len(theta)):
res[i] = (X_b.dot(theta) - y).dot(X_b[:,i])
return res / len(X_b)
def gradient_descent(X_b, y, initial_theta, eta, n_iter=1e4, epsilon=1e-8):
theta = initial_theta
cur_iter = 0
while cur_iter < n_iter:
gradient = dJ(theta, X_b, y)
last_theta = theta
theta = theta - eta * gradient
if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
break
cur_iter += 1
return theta
4.3 测试
4.3.1 只有一个特征的测试数据
import numpy as np
import matplotlib.pyplot as plt
# 使用随机数测试
np.random.seed(999)
x = 2 * np.random.random(size=100)
y = x * 5. + 9. + np.random.normal(size=100)
随机数在二维平面上是这样的:

创建样本数据X_b和参数theta:
X = x.reshape(-1, 1) # X.shape : (100, 1)
X_b = np.hstack([np.ones((len(x), 1)), x.reshape(-1, 1)]) # 添加X0
print(X_b.shape)
initial_theta = np.zeros(X_b.shape[1])
print(initial_theta.shape)
eta = 0.01
theta = gradient_descent(X_b, y, initial_theta, eta)
print(theta)
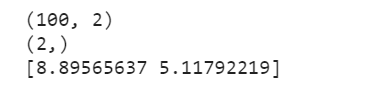
theta_0 大约为8.90, theta_1 大约为5.12,计算的结果和我们最初设置的随机数的y = x * 5. + 9. + np.random.normal(size=100)差不多
4.3.2 有两个特征的测试数据
np.random.seed(999)
x_1 = 2 * np.random.random(size=100)
x_2 = 8 * np.random.random(size=100)
y = 9. + 5. * x_1 + 8. * x_2 + np.random.normal(size=100)
ax = plt.axes(projection='3d')
ax.scatter3D(x_1, x_2, y)
plt.show()
随机数在三维空间中是这样滴:

测试:
X_b = np.hstack([np.ones((len(x), 1)), x_1.reshape(-1, 1), x_2.reshape(-1, 1)])
print(X_b.shape)
initial_theta = np.zeros(X_b.shape[1])
print(initial_theta.shape)
eta = 0.01
theta = gradient_descent(X_b, y, initial_theta, eta)
print(theta)

theta_0 大约为9.00, theta_1大约为4.90, theta_2约为8.00,对比我们之前设置的函数中的参数大致一样。
5.总结
到这儿就把梯度下降的一些内容整理的差不多了,由于我也是初学者,如果有错误或不足,欢迎大家指正!
梯度下降在一般用来寻找函数的最小值,但有可能找到的不是全局最小值而使局部最小值。
以下为废话:
感觉写完这篇博文我把线代矩阵运算的基本知识复习了一遍。
这里再多说一句,吴恩达老师的机器学习真的是经典,B站上也有各大up主上传的视频课,视频地址:地址
虽然视频是很多年前录的,但是理论知识是通用的,我觉得吴恩达老师的理论知识讲的很好。现在很多项目都是用python来做了,github上也有很多开源的项目,大家可以来练练手。
还有一个大佬整理的学习笔记:地址
我还想啰嗦一句,每个人的学习方法不同,所以学习资料啊大家都看情况使用,比如视频课,有的人觉得看视频学习效果好,有的人觉得看书学习效果好,这都是因人而异,大家在学习的时候一定要根据自身情况制定适合自己的学习方法。
我之前也是随大流,大家怎么学我就怎么学,大二上机器学习的课(我们学校的机器学习课程很水)我就是看大家都看吴恩达老师的视频课,我也跟着大家看视频课,但后来发现我看完之后并没有把知识学到脑子里,效果并不理想,但当时并没有想着要调整学习方法,也没有想着要好好学,后来就把machine learning的课程放下了。
时隔一年,脑子终于灵光了,也对机器学习越来越感兴趣了,因此又重新拾起这门课程。就我个人而言,我不是很适合一直看视频学,我反而适合看看书看看别人整理的文字笔记什么的,看视频总让我觉得知识都没进脑子。当然最最最最重要的是:敲代码练习!!!!! 一定一定要练习,练习可以检验你知识的掌握程度,帮你查漏补缺,反正就是一定要练习!
然后就是我自己也准备考研,我之前总觉得要考研就要用大量的时间去学要考的知识,但我现在觉得每天花点时间学点自己感兴趣的知识内容,敲敲代码写写项目整理博客会让我很开心,虽然复习的时间少了,但很值得。
好啦!废话结束!希望看到这篇博客的朋友都能对机器学习越来越感兴趣,都能把machine learning学得特别棒!
