MATLAB 数据分析
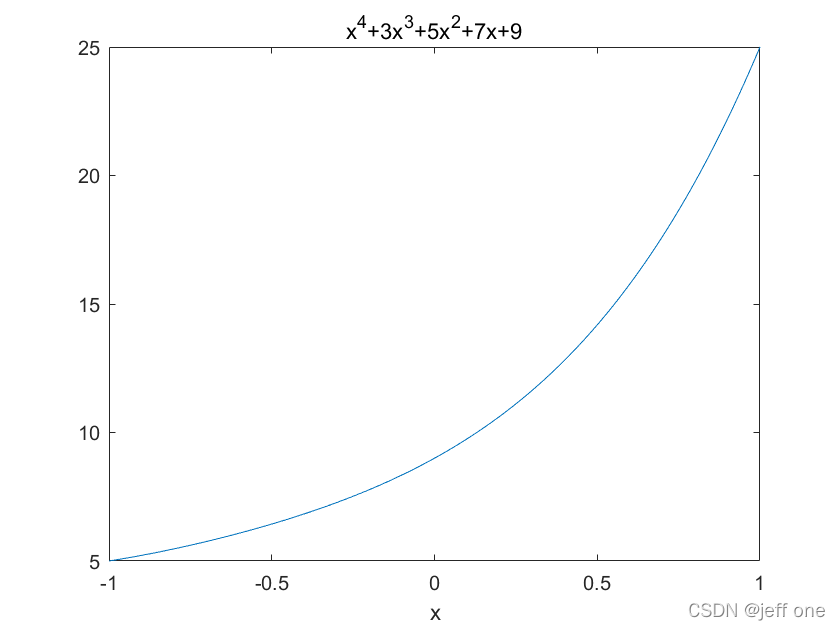
多项式的估值,可用polyval函数:
x=-1:0.01:1; %生成自变量
g=[1 3 5 7 9]; %函数对应的多项式
h=polyval(g,x); %进行估值运算
plot(x,h); %将估值运算结果对自变量作图
xlabel('x');
title('x^4+3x^3+5x^2+7x+9');
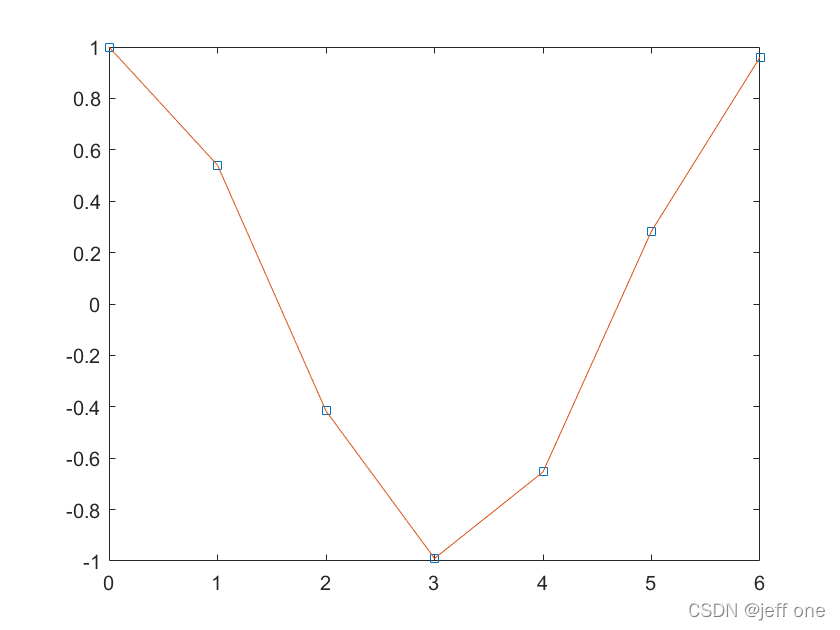
分段线性插值:
例如,用interp1对cos(x)进行分段线性插值
x=0:2*pi;
y=cos(x)
xx=0:0.5:2*pi;
yy=interp1(x,y,xx);
plot(x,y,'s',xx,yy)
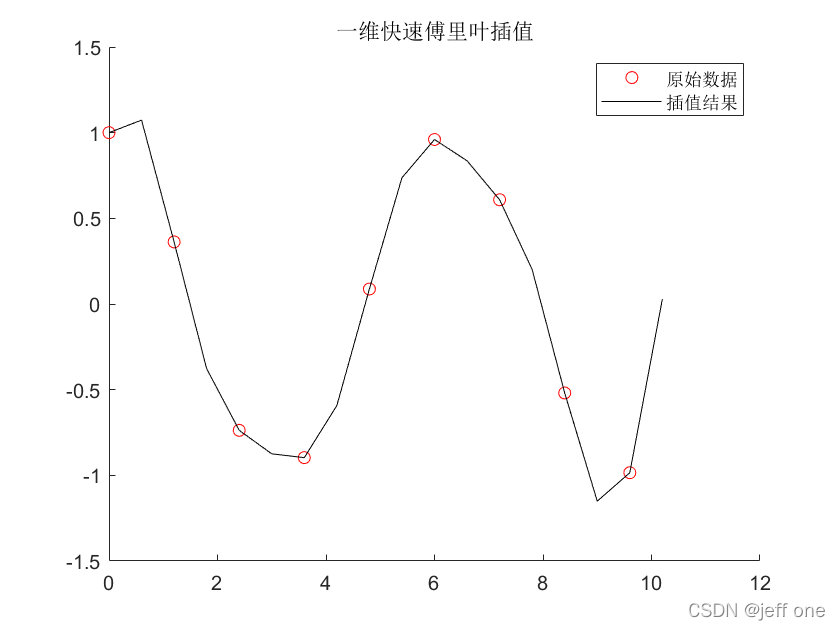
一维快速傅里叶插值:
可用interpft()函数
x=0:1.2:10;
y=cos(x);
n=2*length(x); %增采样1倍
yi=interpft(y,n); %一维快速傅里叶插值
xi=0:0.6:10.4;
hold on;
plot(x,y,'ro'); %画图
plot(xi,yi,'k-');
title('一维快速傅里叶插值');
legend('原始数据','插值结果');
快速fourier算法:
可对周期分布的数据进行插值,例如,用interpft函数对cos函数插值
x=0:2*pi;
y=cos(x);
z=interpft(y,15);
xx=linspace(0,2*pi,15); %生成0~2pi之间的15个线性等分点
plot(x,y,'-o',xx,z,':o')

二维插值:
当被插值函数为二元函数时,用二维插值
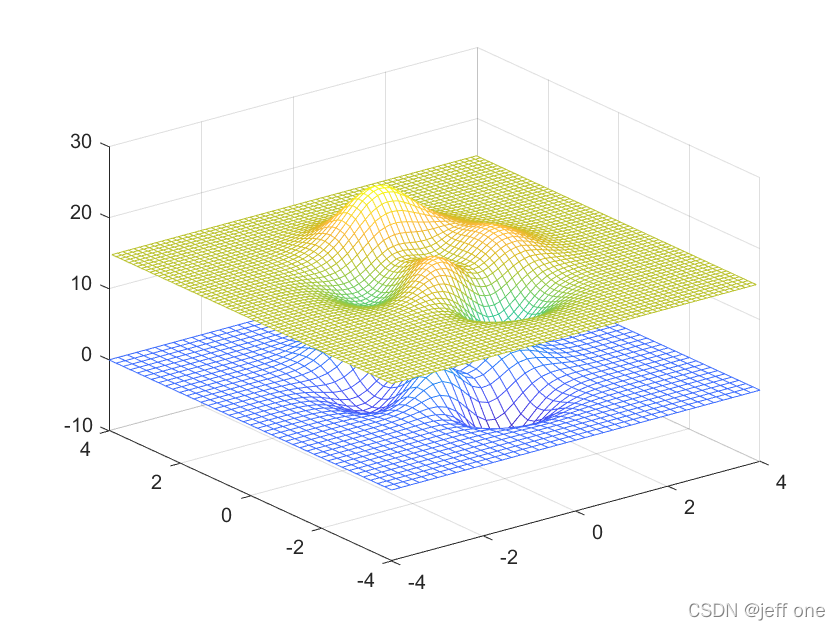
[X,Y]=meshgrid(-4:.20:4); %产生已知的数据栅格点
Z=peaks(X,Y); %计算已知点的函数值
[XI,YI]=meshgrid(-4:.120:4); %产生更精密的插值点
ZI=interp2(X,Y,Z,XI,YI);
mesh(X,Y,Z),hold,mesh(XI,YI,ZI+15)
hold off
aixs([-4 4 -4 4 -10 30])