时间序列回归的渐进性 --潘登同学的计量经济学笔记
文章目录
平稳与弱相关
平稳过程
简单来说,对于某个时间序列(随机过程),如果我们从这个序列中任取一个随机变量集,并把这个序列向前移动 h h h个时期,那么其联合概率分布仍保持不变。 其规范定义如下
平稳随机过程
对于随机过程 { x t : t = 1 , 2 , … } \{x_t:t=1,2,\ldots\} {xt?:t=1,2,…},如果对于每一个时间指标集 1 ≤ t 1 < t 2 < ? < t m 1\leq t_1<t_2<\cdots<t_m 1≤t1?<t2?<?<tm?和任意整数 h ≥ 1 h\geq 1 h≥1, ( x t 1 , x t 2 , … , x t m ) (x_{t_1},x_{t_2},\ldots,x_{t_m}) (xt1??,xt2??,…,xtm??)的联合分布都与 ( x t 1 + h , x t 2 + h , … , x t m + h ) (x_{t_1+h},x_{t_2+h},\ldots,x_{t_m+h}) (xt1?+h?,xt2?+h?,…,xtm?+h?)的联合分布相同,那么这个随机过程就是平稳的
不平稳的随机过程称为非平稳过程,因为平稳性是基础的随机过程的一个方面而不是可以单独实现的,所以我们很难判断所搜集到的数据是否由一个平稳过程生成。 但是,要指出某些序列不是平稳却比较容易。
协方差平稳
对于一个具有有限二阶矩 [ E ( x t 2 ) < ∞ ] [E(x^2_t)<\infty] [E(xt2?)<∞]的随机过程, { x t : t = 1 , 2 , ? ? } \{x_t:t=1,2,\cdots\} {xt?:t=1,2,?},若
- E ( x t ) E(x_t) E(xt?)为常数
- V a r ( x t ) Var(x_t) Var(xt?)为常数
- 对任何 t t t, h ≥ 1 h\geq 1 h≥1, C o v ( x t , x t + 1 ) Cov(x_t,x_{t+1}) Cov(xt?,xt+1?)仅取决于 h h h,而不取决于 t t t
则称他为协方差平稳
平稳性有什么用?
在技术层面上,平稳性简化了大树定律和中心极限定理的表述。在操作层面上,如果我们想通过回归分析掌握两个或多个变量之间的关系,就需要假定某种跨时期的平稳性。如果允许两个变量之间的关系在不同时期随意变化,那么,在只能得到时间序列的单个实现的情况下,我们就无法知道一个变量的变化如何影响另一个变量。
弱相关时间序列
弱相关则是关心随着 h h h的增大, x k x_k xk?与 x k + h x_{k+h} xk+h?多大程度的相关。
弱相关
粗略地讲,对于一个平稳时间序列过程 { x t : t = 1 , 2 , 3 , … } \{x_t:t=1,2,3,\ldots\} {xt?:t=1,2,3,…},若随着 h h h的无限增大, x k x_k xk?与 x k + h x_{k+h} xk+h?“近乎独立”,则称之为若相关
渐进无关
对于协方差平稳序列来说,随着 h → ∞ , C o r r ( x t , x t + h ) → 0 h\to\infty,Corr(x_t,x_{t+h})\to 0 h→∞,Corr(xt?,xt+h?)→0,被称为渐进无关的
-
考虑如下随机过程
x t = e t + α 1 e t ? 1 x_t = e_t + \alpha_1e_{t-1} xt?=et?+α1?et?1?
其中 { e t : t = 0 , 1 , … } \{e_t:t=0,1,\ldots\} {et?:t=0,1,…}是均值为0和方差为 σ e 2 \sigma^2_e σe2?的独立同分布序列。该过程也被称为一阶移动平均过程MA(1)观察一期内的变化
C o v ( x t , x t + 1 ) = α 1 V a r ( e t ) = α 1 σ e 2 ∵ V a r ( x t ) = ( 1 + α 1 2 ) σ e 2 ∴ C o r r ( x t , x t + 1 ) = α 1 1 + α 1 2 Cov(x_t,x_{t+1}) = \alpha_1 Var(e_t) = \alpha_1 \sigma^2_e \\ \because Var(x_t) = (1 + \alpha_1^2)\sigma^2_e \\ \therefore Corr(x_t,x_{t+1}) = \frac{\alpha_1}{1 + \alpha_1^2} Cov(xt?,xt+1?)=α1?Var(et?)=α1?σe2?∵Var(xt?)=(1+α12?)σe2?∴Corr(xt?,xt+1?)=1+α12?α1??
而一旦到达两期及以上时,这些变量都是无关的。因此MA(1)是平稳的弱相关序列 -
考虑如下一阶自回归过程
y t = ρ 1 y t ? 1 + e t y_t = \rho_1y_{t-1} + e_t yt?=ρ1?yt?1?+et?
其中 { e t : t = 0 , 1 , … } \{e_t:t=0,1,\ldots\} {et?:t=0,1,…}是均值为0和方差为 σ e 2 \sigma^2_e σe2?的独立同分布序列,同时还假定 e t e_t et?独立于 y 0 y_0 y0?和 E ( y 0 ) = 0 E(y_0)=0 E(y0?)=0。该过程也被称为一阶自回归过程AR(1)AR(1)过程弱相关的IG关键假定是稳定性条件 ∣ ρ 1 ∣ < 1 |\rho_1|<1 ∣ρ1?∣<1。一旦满足条件,我们称 { y t } \{y_t\} {yt?}是一个稳定的AR(1)过程
观察稳定的AR(1)过程一期内的变化( ∵ E ( y t ) = 0 , E ( y t ) = E ( y t ? 1 ) ; ρ 1 ≠ 1 \because E(y_t)=0,E(y_t)=E(y_{t-1}); \rho_1\neq 1 ∵E(yt?)=0,E(yt?)=E(yt?1?);ρ1??=1)
V a r ( y t ) = ρ 1 2 V a r ( y t ? 1 ) + V a r ( e t ) ∴ σ y 2 = σ e 2 1 ? ρ 1 2 Var(y_t) = \rho_1^2 Var(y_{t-1}) + Var(e_t) \\ \therefore \sigma_y^2 = \frac{\sigma^2_e}{1-\rho_1^2} Var(yt?)=ρ12?Var(yt?1?)+Var(et?)∴σy2?=1?ρ12?σe2??
利用反复迭代,可以得到 y t 与 y t + h y_t与y_{t+h} yt?与yt+h?的协方差
y t + h = ρ 1 h y t + ρ 1 h ? 1 e t + 1 + ? + ρ 1 e t + h ? 1 + e t + h C o v ( y t , y t + h ) = E ( y t , y t + h ) = ρ 1 h E ( y t 2 ) + ρ 1 h ? 1 E ( y t e t + 1 ) + ? + ρ 1 E ( y t e t + h ? 1 ) + E ( y t e t + h ) = ρ 1 h E ( y t 2 ) = ρ 1 h σ y 2 C o r r ( y t . y t + h ) = C o v ( y t , y t + h ) σ y 2 = ρ 1 h y_{t+h} = \rho_1^h y_t + \rho_1^{h-1} e_{t+1} + \cdots + \rho_1 e_{t+h-1} + e_{t+h} \\ \quad\\ \begin{aligned} Cov(y_t,y_{t+h}) &= E(y_t,y_{t+h}) = \rho_1^h E(y_t^2) + \rho_1^{h-1} E(y_t e_{t+1}) + \cdots + \rho_1 E(y_t e_{t+h-1}) + E(y_t e_{t+h}) \\ &= \rho_1^h E(y_t^2) = \rho_1^h \sigma_y^2 \end{aligned}\\ \quad\\ Corr(y_t.y_{t+h}) = \frac{Cov(y_t,y_{t+h})}{\sigma_y^2} = \rho_1^h yt+h?=ρ1h?yt?+ρ1h?1?et+1?+?+ρ1?et+h?1?+et+h?Cov(yt?,yt+h?)?=E(yt?,yt+h?)=ρ1h?E(yt2?)+ρ1h?1?E(yt?et+1?)+?+ρ1?E(yt?et+h?1?)+E(yt?et+h?)=ρ1h?E(yt2?)=ρ1h?σy2??Corr(yt?.yt+h?)=σy2?Cov(yt?,yt+h?)?=ρ1h?
随着 h → ∞ , ρ 1 h → ∞ h\to\infty, \rho_1^h\to\infty h→∞,ρ1h?→∞,所以稳定的AR(1)过程是弱相关的
平稳与弱相关的误区
前面的两个例子中,两个都是协方差平稳的,随后推导出了弱相关; 但并非意味着协方差平稳是弱相关的必要条件; 对于之前的趋势序列,如 y t = α 1 t + e t y_t = \alpha_1 t + e_t yt?=α1?t+et?,他显然是非平稳的(均值方差不固定),但也可能是弱相关的。
如果一个序列是弱相关的,而且围绕着其时间趋势是平稳的,我们就称之为趋势——平稳过程
OLS的渐进性
与之前推导横截面的渐进性作用相似,我们要借助OLS的大样本性质,来更一般地证明OLS的合理性。
假定TS.1’
线性与弱相关
除了增加假定 { ( X t , y t ) : t = 1 , 2 , … } \{(X_t,y_t): t=1,2,\ldots\} {(Xt?,yt?):t=1,2,…}是平稳和弱相关的之外,假定TS.1’与Ts.1完全相同。具体而言,大数定律和中心极限定理可适用于样本均值
假定TS.2’
无完全共线性
与假定TS.2’相同
假定TS.3’
零条件均值
解释变量 X t = { x t 1 , x t 2 , … , x t k } X_t = \{x_{t1},x_{t2},\ldots,x_{tk}\} Xt?={xt1?,xt2?,…,xtk?}是同期外生的: E ( u t ∣ X t ) = 0 E(u_t|X_t)=0 E(ut?∣Xt?)=0
这个假定比TS.3弱得多,因为这个假定不像TS.3对 u t u_t ut?与其他时期解释变量之间的关系做任何限制。但是根据平稳性,若同期外生性对某一时期成立,则对所有时期都成立。这个假定没有控制严格外生,借助于OLS大样本性质,能一定程度上解决被解释变量对未来解释变量的反馈作用
OLS的一致性
在假定TS.1’-3’成立时,OLS估计量是一致的(不一定无偏):
p
l
i
m
β
j
^
=
β
j
,
j
=
0
,
1
,
2
,
…
,
k
plim \hat{\beta_j} = \beta_j, j=0,1,2,\ldots,k
plimβj?^?=βj?,j=0,1,2,…,k
举个例子
考虑AR(1)模型
y
t
=
β
0
+
β
1
y
t
?
1
+
u
t
y_t = \beta_0 + \beta_1 y_{t-1} + u_t
yt?=β0?+β1?yt?1?+ut?
其中,在给定y的所有过去值时,误差
u
t
u_t
ut?的期望值为0
E
(
u
t
∣
y
t
?
1
,
y
t
?
2
,
?
?
)
=
0
E(u_t|y_{t-1},y_{t-2},\cdots) = 0
E(ut?∣yt?1?,yt?2?,?)=0
将上面两个方程结合起来,意味着
E
(
y
t
∣
y
t
?
1
,
y
t
?
2
,
…
)
=
E
(
y
t
∣
y
t
?
1
)
=
β
0
+
β
1
y
t
?
1
E(y_t|y_{t-1},y_{t-2},\ldots) = E(y_t|y_{t-1}) = \beta_0 + \beta_1 y_{t-1}
E(yt?∣yt?1?,yt?2?,…)=E(yt?∣yt?1?)=β0?+β1?yt?1?
该结论非常重要,它意味着,一旦控制了y的一期滞后,y的更高阶滞后都不会影响y的期望值。 既然
X
t
只
包
含
y
t
?
1
X_t只包含y_{t-1}
Xt?只包含yt?1?,方程便意味着假定TS.3’成立,而无偏性所需的严格外生假定却不成立,因为所有时期的解释变量集包含除了最后一期之外的所有y值
(
y
0
,
y
1
,
…
,
y
n
?
1
)
(y_0,y_1,\ldots,y_{n-1})
(y0?,y1?,…,yn?1?),而TS.3要求所有的时期t,
u
t
u_t
ut?都与
y
0
,
y
1
,
?
?
,
y
n
?
1
y_0,y_1,\cdots,y_{n-1}
y0?,y1?,?,yn?1?之中任意的一个无关,而AR(1)模型满足不了这个要求。
因为在AR(1)模型中, y t 与 u t y_t与u_t yt?与ut?一定相关, C o v ( y t , u t ) = V a r ( u t ) > 0 Cov(y_t,u_t) = Var(u_t) > 0 Cov(yt?,ut?)=Var(ut?)>0。 为了使弱相关条件成立,我们必须假定 ∣ β 1 ∣ < 1 |\beta_1|<1 ∣β1?∣<1,如果这个条件成立,根据OLS的一致性,那么模型得到的OLS估计量便是 β 0 和 β 1 \beta_0和\beta_1 β0?和β1?的一致估计量。不幸的是, β 1 ^ \hat{\beta_1} β1?^?是右偏的。而且,若样本容量比较小,或者 β 1 \beta_1 β1?接近1,则偏误可能会很大。 对大样本来说, β 1 ^ \hat{\beta_1} β1?^?应该是 β 1 \beta_1 β1?的一个较好估计值
假定TS.4’
同方差
误差是同期同方差的,即对所有的t,都有 V a r ( u t ∣ X t ) = σ 2 Var(u_t|X_t)=\sigma^2 Var(ut?∣Xt?)=σ2
假定TS.5’
无序列相关
对所有的 t ≠ s t\neq s t?=s,有 E ( u t u s ∣ X t , X s ) = 0 E(u_tu_s|X_t,X_s) = 0 E(ut?us?∣Xt?,Xs?)=0
序列相关通常是静态和有限分布滞后回归中遇到的问题: 无法保证不同时期的无法观测因素
u
t
u_t
ut?是无关的。而对于AR(1)模型,TS.5’确实成立,给出证明(假设
s
<
t
s<t
s<t):
∵
u
s
=
y
s
?
β
0
?
β
1
y
s
?
1
\because u_s = y_s - \beta_0 - \beta_1 y_{s-1}
∵us?=ys??β0??β1?ys?1?
因为
u
s
u_s
us?是
t
t
t时期之前
y
y
y的函数,所以
u
t
与
u
s
u_t与u_s
ut?与us?无关
E
(
u
t
∣
u
s
,
y
t
?
1
,
y
s
?
1
)
=
0
∴
E
(
u
t
u
s
∣
u
s
,
y
t
?
1
,
y
s
?
1
)
=
u
t
E
(
u
t
∣
u
s
,
y
t
?
1
,
y
s
?
1
)
=
0
E(u_t|u_s,y_{t-1},y_{s-1}) = 0 \\ \therefore E(u_tu_s|u_s,y_{t-1},y_{s-1}) = u_t E(u_t|u_s,y_{t-1},y_{s-1}) = 0
E(ut?∣us?,yt?1?,ys?1?)=0∴E(ut?us?∣us?,yt?1?,ys?1?)=ut?E(ut?∣us?,yt?1?,ys?1?)=0
根据迭代期望法则,
E
[
Y
∣
X
]
=
E
[
E
(
Y
∣
X
,
Z
)
∣
X
]
E[Y|X] = E[E(Y|X,Z)|X]
E[Y∣X]=E[E(Y∣X,Z)∣X]
E
(
u
t
u
s
∣
y
t
?
1
,
y
s
?
1
)
=
0
E(u_tu_s|y_{t-1},y_{s-1}) = 0
E(ut?us?∣yt?1?,ys?1?)=0
所以只要模型中只有一期滞后,误差就一定是序列无关的
OLS的渐近正态性
在假定TS.1’到TS.5’下,OLS估计量是渐近正态分布的。而且,通常的OLS标准误,t统计量、F统计量和LM统计量都是渐近有效的


强相关时间序列
上面的都是在弱相关时间序列下,常见的OLS推断程序比经典线性模型假定都成立,那么强相关呢?
高度持续性时间序列
在简单的AR(1)模型中,设
ρ
1
=
1
\rho_1 = 1
ρ1?=1
y
t
=
y
t
?
1
+
e
t
(
?
)
y_t = y_{t-1} + e_t \qquad (*)
yt?=yt?1?+et?(?)
其中
{
e
t
:
t
=
0
,
1
,
…
}
\{e_t:t=0,1,\ldots\}
{et?:t=0,1,…}是均值为0和方差为
σ
e
2
\sigma^2_e
σe2?的独立同分布序列,同时还假定
e
t
e_t
et?独立于
y
0
y_0
y0?和
E
(
y
0
)
=
0
E(y_0)=0
E(y0?)=0
该过程被称为一个随机游走,很好理解,
t
t
t时期的
y
t
y_t
yt?等于上一期的
y
t
?
1
y_{t-1}
yt?1?加上一个独立于
y
t
?
1
y_{t-1}
yt?1?的零均值随机变量。 求出
y
t
y_t
yt?的均值
E
(
y
t
)
=
E
(
e
t
)
+
E
(
e
t
?
1
)
+
?
+
E
(
e
1
)
+
E
(
y
0
)
=
E
(
y
0
)
,
?
t
≥
1
E(y_t) = E(e_t) + E(e_{t-1}) + \cdots + E(e_1) + E(y_0) = E(y_0), \forall t \geq 1
E(yt?)=E(et?)+E(et?1?)+?+E(e1?)+E(y0?)=E(y0?),?t≥1
因此,随机游走的期望不取决于t; 然而,随机游走的方差却随着时间的推移而变化,假设
V
a
r
(
y
0
)
=
0
Var(y_0)=0
Var(y0?)=0
V
a
r
(
y
t
)
=
V
a
r
(
e
t
)
+
V
a
r
(
e
t
?
1
)
+
?
+
V
a
r
(
e
1
)
=
σ
e
2
t
Var(y_t) = Var(e_t) + Var(e_{t-1}) + \cdots + Var(e_1) = \sigma^2_e t
Var(yt?)=Var(et?)+Var(et?1?)+?+Var(e1?)=σe2?t
随机游走的方差是时间的线性函数,其显然是不平稳的…
更重要的是,随机游走表现出了高度持续性的行为,这是因为现在的y值对于决定遥远未来的y值都有非常重要的作用
y
t
+
h
=
e
t
+
h
+
e
t
+
h
?
1
+
?
+
e
t
+
1
+
y
t
E
(
y
t
+
h
∣
y
t
)
=
y
t
,
?
h
≥
1
y_{t+h} = e_{t+h} + e_{t+h-1} + \cdots + e_{t+1} + y_t \\ E(y_{t+h}|y_t) = y_t, \forall h \geq 1
yt+h?=et+h?+et+h?1?+?+et+1?+yt?E(yt+h?∣yt?)=yt?,?h≥1
这意味着,无论我们展望多远,
y
t
+
h
y_{t+h}
yt+h?的最好预测值总是今天的
y
t
y_t
yt?值。(回想到: 半强有效市场假说, 最好的预期就是当下的价格)
当
{
y
t
}
\{y_t\}
{yt?}服从随机游走模式,对于
t
t
t很大的情形,
y
t
与
y
t
+
h
y_t与y_{t+h}
yt?与yt+h?的相关性接近于1。如果
V
a
r
(
y
0
)
=
0
Var(y_0)=0
Var(y0?)=0,可以证明
C
o
r
r
(
y
t
,
y
t
+
h
)
=
t
t
+
h
Corr(y_t,y_{t+h}) = \sqrt{\frac{t}{t+h}}
Corr(yt?,yt+h?)=t+ht??
他们的相关程度取决于
t
t
t,也说明这不是平稳过程;
- 固定t,当h趋于无穷时,相关性趋于0
- t越大,这种相关性随着h变大而趋于0的速度会越慢
单位根过程
随机游走是单位根过程的一个特例,因为 ρ 1 = 1 \rho_1=1 ρ1?=1所以称为单位根…
更一般的单位根过程可以由 ( ? ) (*) (?)生成,其中的 { e t } \{e_t\} {et?}可以是一个普通的弱相关序列。而当 { e t } \{e_t\} {et?}不是一个独立同分布序列的时候,前面推导的随机游走性质就不成立;
从政策角度来看,知道一个经济时间序列是否具有高度持续性往往很重要。 以GDP为例,如果GDP是渐近无关的,那么下一年的GDP水平最多与很多年前(如30年前的GDP)有弱相关关系。这意味着一项很久以前作用于GDP的政策,在现在几乎没有什么持续影响。 相反,如果GDP是强相关的,那么明年的GDP可以与很多年前的GDP都高度相关。于是,我们应该认识到,一项造成GDP离散变化的政策也可能具有持久的影响
带截距的随机游走
重要一点,不要混淆趋势行为与高度持续性行为。 有趋势行为不一定是高度持续性的。 而高度持续性的序列往往包含了明显的趋势,描述这一情形的模型是带截距的随机游走
y
t
=
α
0
+
y
t
?
1
+
e
t
y_t = \alpha_0 + y_{t-1} + e_t
yt?=α0?+yt?1?+et?
以下是其一个实现
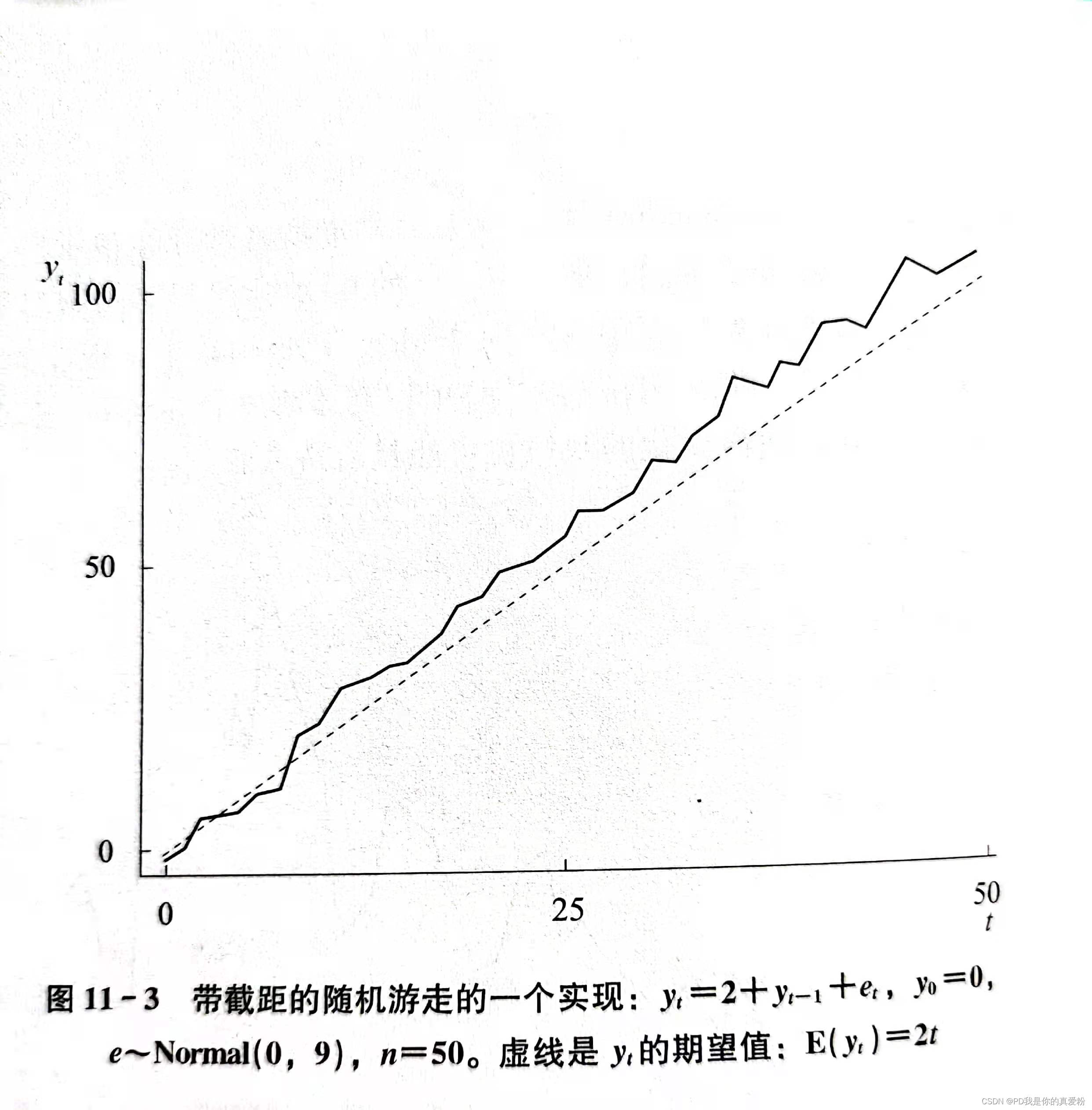
高度持续时间序列的变换
可以用单位根过程表示一类高度持续性的时间序列,我们可以做一些变化,使其变为弱相关
- 弱相关过程为称为零阶单整(integrated of order zero)或 I ( 0 ) I(0) I(0)
- 随机游走被称为一阶单整(integrated of order one)或 I ( 1 ) I(1) I(1)
I ( 0 ) I(0) I(0)表明无需处理,这个序列的均值就已经满足标准的极限定理; 而 I ( 1 ) I(1) I(1)意味着这个过程的一阶差分便是弱相关的(通常是平稳的)。 I ( 1 ) I(1) I(1)也被称为差分平稳过程
△
y
t
=
y
t
?
y
t
?
1
=
e
t
\triangle y_t = y_t - y_{t-1} = e_t
△yt?=yt??yt?1?=et?
一阶差分后的序列
{
△
y
t
:
t
=
2
,
3
,
…
}
\{\triangle y_t: t=2,3,\ldots\}
{△yt?:t=2,3,…}实际上一个独立同分布序列,因为
{
e
t
}
\{e_t\}
{et?}是一个弱相关过程,则
{
△
y
t
}
\{\triangle y_t\}
{△yt?}也是弱相关的。 在方程中一般不写
△
\triangle
△,而是用cy或dy来表示,如y表示价格,那么就是cprice或dprice
判断时间序列是否为I(1)
简单的方法就是去计算别解释变量的一阶自相关系数
ρ
1
=
C
o
r
r
(
y
t
,
y
t
?
1
)
\rho_1 = Corr(y_t,y_{t-1})
ρ1?=Corr(yt?,yt?1?)
当
ρ
1
>
0.9
\rho_1>0.9
ρ1?>0.9,就需要进行差分
更一般的检验方法,以后再说…
动态完备模型和无序列相关
前面说到,AR(1)其实是满足序列无关的: 而假定不存在序列相关,实际上等同于假定 E ( y t ∣ y t ? 1 , y t ? 2 , … ) E(y_t|y_{t-1},y_{t-2},\ldots) E(yt?∣yt?1?,yt?2?,…)中只包含y的一期滞后(注意:这不是普遍性结论,这只是针对 y t = β 0 + β 1 y t ? 1 + u t y_t = \beta_0 + \beta_1 y_{t-1} + u_t yt?=β0?+β1?yt?1?+ut?,因为模型中解释变量只有一个)
进而我们可以证明: 模型只要设定合理,就是序列无关的
动态完备模型
动态完备模型可以理解成设定合理的模型
-
考虑一个简单情形
y t = β 0 + β 1 z t + u t y_t = \beta_0 + \beta_1 z_t +u_t yt?=β0?+β1?zt?+ut?
如果存在
E ( y t ∣ z t , y t ? 1 , z t ? 1 , ? ? ) = E ( y t ∣ z t ) = β 0 + β 1 z t E(y_t|z_t,y_{t-1},z_{t-1},\cdots) = E(y_t|z_t) = \beta_0 + \beta_1 z_t E(yt?∣zt?,yt?1?,zt?1?,?)=E(yt?∣zt?)=β0?+β1?zt?
上式的第一个等式很重要: 一旦控制了 z t z_t zt?, y 或 z y或z y或z的滞后项无助于解释当前的y,当满足这个条件,这么模型就是动态完备模型。上式其实包含了一个重要假定
E ( u t ∣ z t , y t ? 1 , z t ? 1 , ? ? ) = 0 E(u_t|z_t,y_{t-1},z_{t-1},\cdots) = 0 E(ut?∣zt?,yt?1?,zt?1?,?)=0 -
考虑一般情形
y = β 0 + β 1 x t 1 + ? + β k x t k + u t y = \beta_0 + \beta_1 x_{t1} + \cdots + \beta_k x_{tk} + u_t y=β0?+β1?xt1?+?+βk?xtk?+ut?
其中,解释变量 X t = ( x t 1 , ? ? , x t k ) X_t = (x_{t1},\cdots,x_{tk}) Xt?=(xt1?,?,xtk?)可能包含也可能不包含 y 或 z y或z y或z的滞后项。 当满足
E ( y t ∣ X t , y t ? 1 , X t ? 1 , ? ? ) = E ( y t ∣ X t ) ? E ( u t ∣ X t , u t ? 1 , X t ? 1 , ? ? ) = 0 E(y_t|X_t,y_{t-1},X_{t-1},\cdots) = E(y_t|X_t) \\ \Leftrightarrow E(u_t|X_t,u_{t-1},X_{t-1},\cdots) = 0 E(yt?∣Xt?,yt?1?,Xt?1?,?)=E(yt?∣Xt?)?E(ut?∣Xt?,ut?1?,Xt?1?,?)=0
这个模型就是一个动态完备模型
动态完备模型是无序列相关
动态完备模型一定满足TS.5’(无序列相关),具体起见,假设
s
<
t
s<t
s<t,利用期望迭代法则
E
(
u
s
u
t
∣
X
t
,
X
s
)
=
E
[
E
(
u
s
u
t
∣
X
t
,
X
s
,
u
s
)
∣
X
t
,
X
s
]
=
E
[
u
s
E
(
u
t
∣
X
t
,
X
s
,
u
s
)
∣
X
t
,
X
s
]
=
0
(
∵
E
(
u
t
∣
X
t
,
X
s
,
u
s
)
=
0
)
=
0
\begin{aligned} E(u_su_t|X_t,X_s) &= E[E(u_su_t|X_t,X_s,u_s)|X_t,X_s] \\ &= E[u_sE(u_t|X_t,X_s,u_s)|X_t,X_s] \\ &= 0 \qquad (\because E(u_t|X_t,X_s,u_s) = 0) \end{aligned} = 0
E(us?ut?∣Xt?,Xs?)?=E[E(us?ut?∣Xt?,Xs?,us?)∣Xt?,Xs?]=E[us?E(ut?∣Xt?,Xs?,us?)∣Xt?,Xs?]=0(∵E(ut?∣Xt?,Xs?,us?)=0)?=0
这个模型就是一个动态完备模型
动态完备模型是无序列相关
动态完备模型一定满足TS.5’(无序列相关),具体起见,假设
s
<
t
s<t
s<t,利用期望迭代法则
E
(
u
s
u
t
∣
X
t
,
X
s
)
=
E
[
E
(
u
s
u
t
∣
X
t
,
X
s
,
u
s
)
∣
X
t
,
X
s
]
=
E
[
u
s
E
(
u
t
∣
X
t
,
X
s
,
u
s
)
∣
X
t
,
X
s
]
=
0
(
∵
E
(
u
t
∣
X
t
,
X
s
,
u
s
)
=
0
)
\begin{aligned} E(u_su_t|X_t,X_s) &= E[E(u_su_t|X_t,X_s,u_s)|X_t,X_s] \\ &= E[u_sE(u_t|X_t,X_s,u_s)|X_t,X_s] \\ &= 0 \qquad (\because E(u_t|X_t,X_s,u_s) = 0) \end{aligned}
E(us?ut?∣Xt?,Xs?)?=E[E(us?ut?∣Xt?,Xs?,us?)∣Xt?,Xs?]=E[us?E(ut?∣Xt?,Xs?,us?)∣Xt?,Xs?]=0(∵E(ut?∣Xt?,Xs?,us?)=0)?
最后书中有一段话,不太理解,先把图贴上,以后应该就能理解了

