PCA
主成分分析(PCA)是一种多变量统计方法,它是最常用的降维方法之一,通过正交变换将一组可能存在相关性的变量数据转换为一组线性不相关的变量,转换后的变量被称为主成分
可以使用两种方法进行PCA,分别是特征分解或奇异值分解(SVD)。PCA旨在找到数据中的主成分,并利用这些主成分表征原始数据,从而达到降维的目的。
算法步骤
假设有m条n维数据
- 将原始数据按列组成n行m列矩阵X
- 将X的每一行(代表一个属性字段)进行零均值化,即减去这一行的均值
- 求出协方差矩阵 C = 1 m X X T C=\frac{1}{m}XX^T C=m1?XXT
- 求出协方差矩阵的特征值以及对应的特征向量
- 将特征向量按对应特征值大小从上到下按列排列成矩阵,取前k行组成矩阵P
- Y = P X Y=PX Y=PX即为降维到k维后的数据
答案解析
PCA是比较常见的线性降维方法,通过线性投影将高维数据映射到低维数据中,所期望的是在投影的维度上,新特征自身的方差尽量大,方差越大特征越有效,尽量使产生的新特征间的相关性越小。
PCA算法的具体操作为对所有的样本进行中心化操作,计算样本的协方差矩阵,然后对协方差矩阵做特征值分解,取最大的n个特征值对应的特征向量构造投影矩阵。
PCA降维之后的维度怎么确定
- 可以利用交叉验证,再选择一个简单的分类器,来选择比较好的k值
- 可以设置一个比重阈值t,比如95%,然后选择满足阈值的最小的k:
说说PCA的优缺点
优点
- 仅仅需要以方差衡量信息量,不受数据集以外的因素影响
- 各主成分之间正交,可消除原始数据成分间的相互影响的因素
- 计算方法简单,主要运算是特征值分解,易于实现
缺点
- 主成分各个特征维度的含义具有一定的模糊性,不如原始样本特征的解释性强
- 方差小的非主成分也可能含有对样本差异的重要信息,因此降维丢弃可能对后续数据处理有影响
- PCA属于有损压缩
推导一个PCA
- 定义初始变量:
假设有样本: X = [ x 1 , x 2 , . . . , x n ] T X=[x_1, x_2, ..., x_n]^T X=[x1?,x2?,...,xn?]T
样本均值: x = 1 n ∑ i = 1 n x i x = \frac{1}{n}\sum^n_{i=1}x_i x=n1?∑i=1n?xi?
样本沿 w w w方向投影的均值: u = 1 n ∑ i = 1 n w T x i u = \frac{1}{n}\sum^n_{i=1}w^Tx_i u=n1?∑i=1n?wTxi?
样本的协方差矩阵: c o v ( X ) = ∑ = 1 n ∑ i = 1 n ( x i ? x ) ( x i ? x ) T cov(X) = \sum=\frac{1}{n}\sum^n_{i=1}(x_i-x)(x_i-x)^T cov(X)=∑=n1?∑i=1n?(xi??x)(xi??x)T - 对样本投影后的方差进行推导化简:
σ
2
=
1
n
∑
i
=
1
n
(
w
T
x
i
?
μ
)
2
\sigma^{2}=\frac{1}{n} \sum_{i=1}^{n}\left(w^{T} x_{i}-\mu\right)^{2}
σ2=n1?∑i=1n?(wTxi??μ)2
=
1
n
∑
i
=
1
n
(
w
T
x
i
?
1
n
∑
i
=
1
n
w
T
x
i
)
2
=\frac{1}{n} \sum_{i=1}^{n}\left(w^{T} x_{i}-\frac{1}{n} \sum_{i=1}^{n} w^{T} x_{i}\right)^{2}
=n1?∑i=1n?(wTxi??n1?∑i=1n?wTxi?)2
=
1
n
∑
i
=
1
n
(
w
T
x
i
?
w
T
(
1
n
∑
i
=
1
n
x
i
)
)
2
=\frac{1}{n} \sum_{i=1}^{n}\left(w^{T} x_{i}-w^{T}\left(\frac{1}{n} \sum_{i=1}^{n} x_{i}\right)\right)^{2}
=n1?∑i=1n?(wTxi??wT(n1?∑i=1n?xi?))2
=
1
n
∑
i
=
1
n
(
w
T
(
x
i
?
x
ˉ
)
)
2
\quad=\frac{1}{n} \sum_{i=1}^{n}\left(w^{T}\left(x_{i}-\bar{x}\right)\right)^{2}
=n1?∑i=1n?(wT(xi??xˉ))2
=
1
n
∑
i
=
1
n
(
w
T
(
x
i
?
x
ˉ
)
)
(
w
T
(
x
i
?
x
ˉ
)
)
T
=\frac{1}{n} \sum_{i=1}^{n}\left(w^{T}\left(x_{i}-\bar{x}\right)\right)\left(w^{T}\left(x_{i}-\bar{x}\right)\right)^{T}
=n1?∑i=1n?(wT(xi??xˉ))(wT(xi??xˉ))T
=
1
n
∑
i
=
1
n
w
T
(
x
i
?
x
ˉ
)
(
x
i
?
x
ˉ
)
T
w
=\frac{1}{n} \sum_{i=1}^{n} w^{T}\left(x_{i}-\bar{x}\right)\left(x_{i}-\bar{x}\right)^{T} w
=n1?∑i=1n?wT(xi??xˉ)(xi??xˉ)Tw
=
w
T
[
1
n
∑
i
=
1
n
(
x
i
?
x
ˉ
)
(
x
i
?
x
ˉ
)
T
]
w
=w^{T}\left[\frac{1}{n} \sum_{i=1}^{n}\left(x_{i}-\bar{x}\right)\left(x_{i}-\bar{x}\right)^{T}\right] w
=wT[n1?∑i=1n?(xi??xˉ)(xi??xˉ)T]w
=
w
T
Σ
w
\quad=w^{T} \Sigma w
=wTΣw
因为
w
T
(
x
i
?
x
)
w^T(x_i-x)
wT(xi??x)的结果是一个实数,是一个
1
x
1
1x1
1x1的矩阵,所以它自身等同于它的转置,也就是下一行变换的原因。而对于要求的
w
w
w就是:
w
=
a
r
g
m
a
x
(
w
T
∑
w
)
w=argmax(w^T\sum{w})
w=argmax(wT∑w)
当然,还要加上约束条件:
w
T
w
=
1
w^Tw=1
wTw=1

LDA
线性判别分析是一种基于有监督学习的降维方式, 将数据集在低维度的空间进行投影,要使得投影后的同类别的数据点间的距离尽可能的靠近,而不同类别间的数据点的距离尽可能的远
LDA的中心思想是什么
最大化类间距离和最小化类内距离
LDA的优缺点
优点
- 在降维过程中可以使用类别的先验知识经验,而像PCA这样的无监督学习则无法使用类别先验知识
- LDA在样本分类信息依赖均值而不是方差的时候,比PCA之类的算法较优
缺点
- LDA不适合对非高斯分布样本进行降维,PCA也有这个问题
- LDA降维最多降到类别数k-1的维数,如果我们降维的维度大于k-1,则不能使用LDA。
- LDA在样本分类信息依赖方差而不是均值的时候,降维效果不好
- LDA可能过度拟合数据
LDA的步骤
假设有m条n维数据
- 计算类内散度矩阵 S w S_w Sw?
- 计算类间散度矩阵 S b S_b Sb?
- 计算矩阵 S w ? 1 S b S^{-1}_wS_b Sw?1?Sb?
- 计算矩阵 S w ? 1 S b S^{-1}_wS_b Sw?1?Sb?的最大的d个特征值和对应的d个特征向量(w_1, w_2, … w_d),得到投影矩阵W
- 对样本集中的每一个样本特征 x i x_i xi?,转化为新的样本 z i = W T x i z_i=W^Tx_i zi?=WTxi?
- 得到输出样本集 D ′ = ( z 1 , y 1 ) , ( z 2 , y 2 ) , . . . , ( z m , y m ) D^{'}=(z1,y1), (z2, y2),..., (zm, ym) D′=(z1,y1),(z2,y2),...,(zm,ym)
推导LDA
-
定义初始变量
假设有 C 1 C_1 C1?, C 2 C_2 C2?两个类别的样本,两类的均值分别为:

我们希望投影之后两类之间的距离尽可能的大,距离表示为:
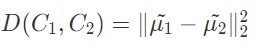
其中 μ ~ 1 , μ ~ 2 \tilde{\mu}_{1}, \tilde{\mu}_{2} μ~?1?,μ~?2?表示两类的中心在w方向上的投影向量:
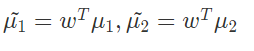
因此需要优化的问题为:
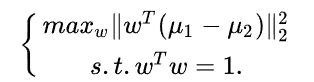
容易发现当w方向与 ( μ 1 ? μ 2 ) (\mu_1-\mu_2) (μ1??μ2?)一致的时候,该距离达到最大值 -
构造目标函数
根据LDA的中心思想——最大化类间距离和最小化类内距离,我们将目标函数定义为类间距离和类内距离的比值:
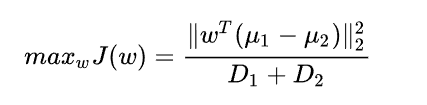
其中w为单位向量, D 1 , D 2 D_1,D_2 D1?,D2?分别表示两类投影后的方差:

因此 J ( w ) J(w) J(w)可以写成:
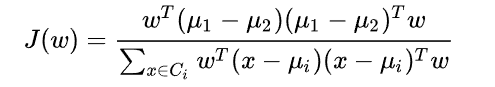

PCA和LDA有什么区别
相同点:
- 两者均可以对数据进行降维
- 两者在降维时均使用了矩阵特征分解的思想
- 两者都假设数据符合高斯分布
不同点:
- LDA是有监督的降维方法,而PCA是无监督的降维方法
- LDA降维最多降到类别数k-1的维数,PCA没有限制
- LDA除了可以用于降维,还可以用于分类
- LDA选择分类性能最好的投影方向,而PCA选择样本点投影具有最大方差的方向


偏差与方差
偏差:偏差衡量了模型的预测值与实际值之间的偏离关系。通常在深度学习中,我们每一次训练迭代出来的新模型,都会拿训练数据进行预测,偏差就反应在预测值与实际值匹配度上
方差:方差描述的是训练数据在不同迭代阶段的训练模型中,预测值的变化波动情况。从数学角度看,可以理解为每个预测值与预测均值差的平方和再求平均数。通常在深度学习训练中,初始阶段模型复杂度不高,为低方差;随着训练量加大,模型逐步拟合训练数据,复杂度开始变高,此时方差会逐渐变高。
SVD
奇异值分解是在机器学习领域广泛应用的算法,它不光可以用于降维算法中的特征分解,还可以用于推荐系统,以及自然语言处理等领域。
SVD也是对矩阵进行分解,但是和特征分解不同,SVD并不要求要分解的矩阵为方阵。假设我们的矩阵A是一个mxn的矩阵,那么我们定义矩阵A的SVD为: A = U ∑ V T A=U\sum{V^T} A=U∑VT,其中U是一个mxm的矩阵, ∑ \sum ∑是一个mxn的矩阵,V是一个nxn的矩阵, U T U = I , V T V = I U^TU=I, V^TV=I UTU=I,VTV=I, 那么 A A T AA^T AAT的特征向量组成的就是我们SVD中的U矩阵
伯努利分布和二项分布的区别
伯努利分布:是假设一个事件只有发生或者不发生两种可能,并且这两种可能是固定不变的。那么,如果假设它发现的概率是p,那么它不发生的概率就是1-p
二项分布:是多次伯努利分布实验的概率分布
