[人工智能]Long-tailed Recognition by Routing Diverse Distribution-Aware Experts

最近看了一篇2021 ICML关于long-tail distributed数据分类问题的文章，觉得很有趣，故写个简单的笔记来记录一下，顺便推广给更多感兴趣的朋友。
首先long-tail distributed数据学习的难度有两点：①、由于尾部数据的数据量通常非常有限，因此对尾部数据进行充分学习是一个难点。②、由于不同class的数据分布差异很大，因此如何使得学习结果尽可能无偏也是一个难点。以往解决long-tail distribution数据学习有两个方法：①、对尾部数据进行重采样或是对头部数据进行欠采样，但是这会导致对尾部数据的过拟合或是对头部数据的欠拟合（对头部数据的欠采样实际上是在训练时浪费了大量有用信息）。②、通过对不同分布进行集成学习的方式，但是作者给出了实验说明这样对尾部数据性能的提升会带来头部数据性能和稳定性的下降。
在本文中，作者将分类问题的学习目标分解成了三个不同的目标：
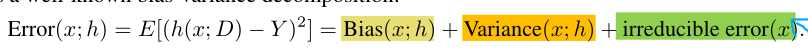其中$x$是输入图像，$h(.)$是分类网络，$D$是训练图像的分布，$Y$是分类结果。那么对于最常见的均方损失就可以分解成：①、网络$h(x)$对数据$x$的分类偏执，即$x$被网络倾向于的分类结果。②、网络$h(x)$对数据$x$的分类方差，即网络对$x$分类的稳定程度。③、数据$x$的不可约损失，即由于$x$在$D$中的分布而产生的损失。那么可以看出，①关系到分类的精度，②关系到分类的稳定性，而③是我们无法改变的，因此下面要着重考虑①和②。

对于n个随机数据集$D^1,D^2,...,D^n$，分别训练n个分类器$h^1,...,h^n$，之后对于图像$x$，第k个分类器对其分类结果为$y^k$，真实值的期望表示为$t$，则有：

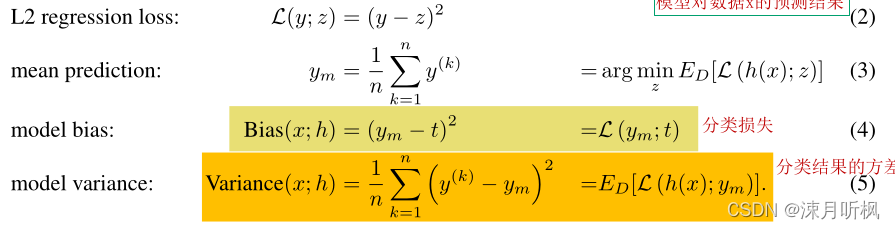
可见对于集成学习的方式进行long-tail distribution数据学习时，其偏执和方差可以公式化成上面的样子。之后，作者在一个long-tail数据集上对多个集成学习模型进行了测试，并将上面两个值展示了出来：

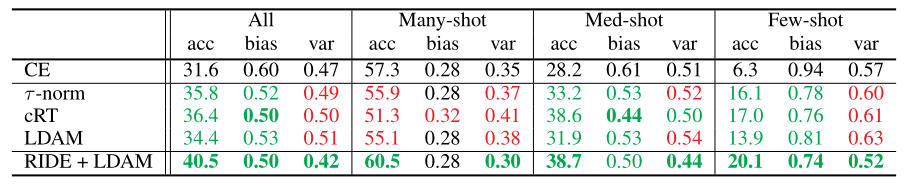
可见，传统的集成学习模型尽管提升了分类精度，但是头部数据无论是偏执还是方差都被大大牺牲。也就是，在最终的分类精度提升有限的情况下，这些模型想按下去第一项，其代价是增加了第二项，然而这并不是我们想要的结果。
通过以上分析，作者提出了两个点：①、通过多专家集成学习的方式来降低所有class的分类方差。②、通过分布多样式损失避免头部数据的偏执降低。③、专家路由，每次分类只启用部分专家，降低计算量。④、专家共享部分网络参数。
通过这些方式，作者不仅提升了整体分类精度，而且没有损害头部数据的分类精度，达到了最理想的效果。

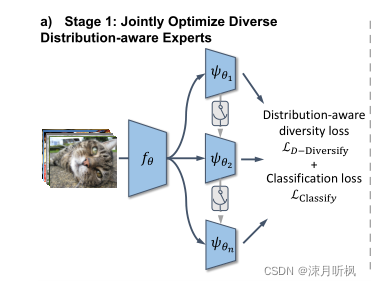
接下来看一下具体的操作。首先是专家的部分参数共享：对于每个专家，可以将其分成CNN部分的特征提取网络和全连接部分的特征分类网络，由于特征提取是对每个图像个体进行的，因此这一部分几乎不会受到数据分布的影响，因此这部分的网络是共享的。而之后的分类网络则是每个专家独自的部分。此外为了避免每个专家成为了全能，作者有意减少了分类网络层数。然后作者会将这些个专家通过分类损失和分布多样性损失进行共同训练。对于分类损失，传统的集成学习的目标是：

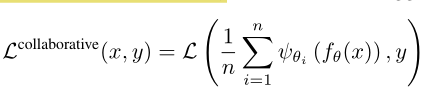
然而作者在这里指出，这种学习目标会使得每个专家之间产生相关性（多个专家共同做一件事），这就相当于变相的削弱了多专家的效果。为了避免产生这种相关性，作者提出了另一种优化目标：

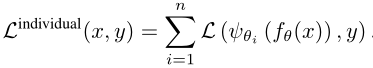
就是说，每个专家都只能靠自己来预测结果，用原文中一句非常形象的话来说就是to do the job well by itself. 由此使得每一个专家在某一个领域（某一个数据分布）可以独当一面。之后为了避免专家们都只关注某一个分布，作者又提出了分布多样性损失：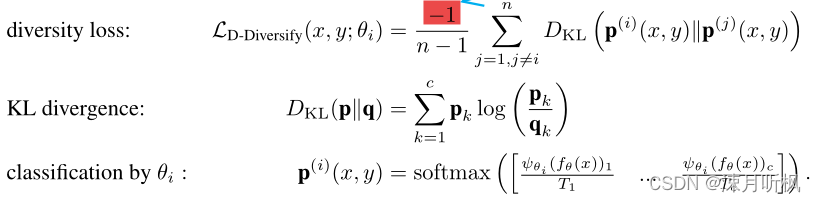
其中$p^i(x,y)$是专家$i$对$x$的预测分布。作者通过最大化多个专家们预测结果分布的KL散度，最大化专家们之间的多样性。其中稍微要说的一点是，最下面公式中的$T_i$与这个类的样本数量正相关，这也很好理解，样本越多，理论上越好学习，那么就不需要那么多专家去学这个方向，应该让更多的专家去学习更难的方向（数据量更少的类）。

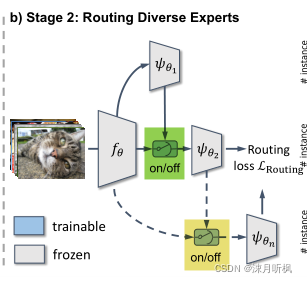
讲完了专家再讲路由：这里之所以要引入路由，是为了避免每次分类时，都启用所有的专家。这里的路由是两层全连接网络，并且在训练路由时，专家的权重保持固定。
首先作者引入了一个指示指标$y_{on}$，意思是：路由输入图像特征$x$和$1k$个专家的分类决策均值，如果这$1k$个专家错分了，而剩下的专家正确分类，就启用第k+1个专家，也就是此时$y_{on}=1$，否则$y_{on}=0$，而每个路由的学习目标就是$y_{on}$。公式化表示：

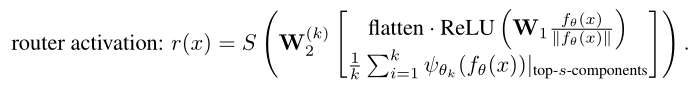
其中$W_1$是输入的图像特征对应的路由网络，所有路由共享这部分网络，$W_2^k$是第$k$个专家对应的路由的网络。其优化目标是：

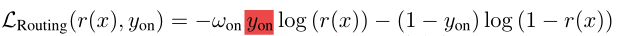
其中${\omega }_{on}$是一个权重参数。路由的作用，用人话来说就是：如果前k个专家不行，那么就打开路由这扇门，让下一个专家进来然后1+k个专家一起商量对策。从这个角度来讲，其实预期叫做是路由，不如叫做switch更形象。

创作挑战赛

新人创作奖励来咯，坚持创作打卡瓜分现金大奖