[人工智能]机器学习（五）——支持向量机（SVM）

一、SVM定义

支持向量机（Support Vector Machine，SVM）：
\qquad 进行二分类问题的学习，设计最优的一个超平面，将两个不同的样本分离开来，这个超平面我们就称它为支持向量机
\qquad 得到最优超平面的学习策略，使间隔（margin）最大化，

二、线性问题

讨论在二维空间的线性可分

如下图所示：

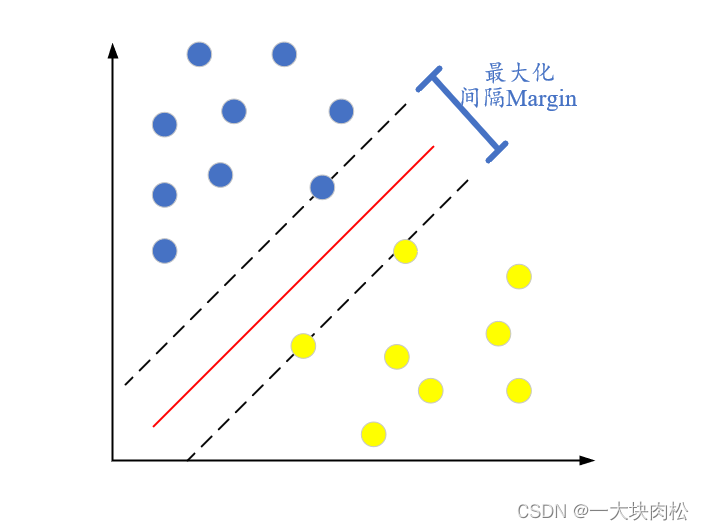
（1）上图中，我们找到具有最大的间隔，当需要测试新的数据时，分类的结果会有更高的可信度。
（2）由图中可知，上下的边界会经过一些样本数据点，这些数据点的位置，决定了间隔的大小，称这些样本数据点为支持向量（Support vector），中间的超平面就称为支持向量机

三、非线性问题

1.问题描述

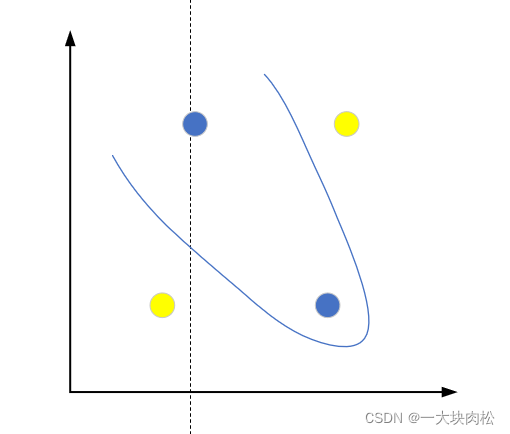
上面的测试用例是在二维空间内线性可分的，然而在现实任务中，训练集样本也并不是都能够存在一个能正确划分两类样本的超平面。例如下图：

\qquad 针对上述问题，我们可以将二维数据利用某种方法映射到三维空间中，这样就可以找到一个超平面将其两类样本分隔开。
\qquad 将数据映射到高维，为了找到合适的超平面，这个特征空间的维度可能很高，甚至无穷维，这个给求取超平面带来了一定的难度，为解决这个问题，核函数横空出世，它避免了求解高维甚至无穷维特征空间中的内积。

2.常用的核函数：

线性核
多项式核
高斯核（又称为RBF核）
拉普拉斯核
Sigmoid核

四、软间隔

1.定义

\qquad 在上面二、三讨论的问题，一直假设的是训练样本在样本空间或特征空间中是线性可分的，即存在一个超平面能将不同类的样本完全划分开。
\qquad 然而在现实任务中，往往很难找到一个合适的核函数使得训练集在特征空间中线性可分，或者说，即使找到一个核函数，能够将训练集样本在线性空间中可分，这也很难保证这个线性可分的结果不是由于过拟合造成的。

化解上述问题的一个办法就是允许支持向量机在一些样本上出错，为此，引入“软间隔”（soft margin）

相对于软间隔，之前们讲的将所有测试数据都区分开来是硬间隔

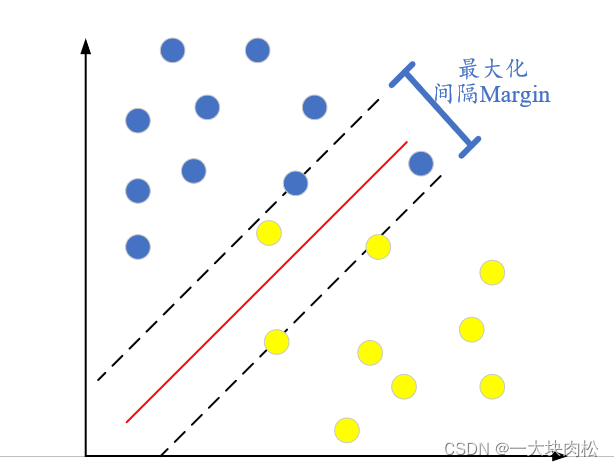
软间隔的目的是：在容错率与间隔距离中找到一个平衡

2.引入损失函数

常见的损失函数：

0/1损失函数
hinge损失函数（铰链损失）
指数损失函数
对率损失函数

引入损失函数之后的支持向量机的求解问题就转化为：

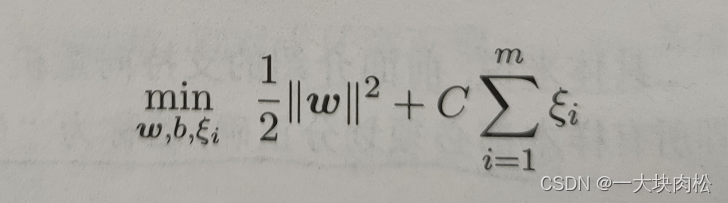
\qquad 上式中，我们可以看出需要考虑两个变量w和损失值 ${\xi }_i$，两者都是越小越好，但是两者相互制约：

\qquad w长度越大，间隔越小，原始数据越不容易出现分类错误，即 ${\xi }_i$和越小；
\qquad w长度越小，间隔越大，原始数据会出现分类错误，即 ${\xi }_i$和越大。
\qquad 因此w和 ${\xi }_i$需要达到平衡，实现两者相加的最小化，达到总体的最优。

\qquad 上面公式，还存在一个常数C
\qquad C的作用是：根据C的大小我们可以控制对损失值 ${\xi }_i$的容忍度，起到惩罚 ${\xi }_i$的作用。
如下：

\qquad 当设置的C越大，则 ${\xi }_i$和就会越大，那么此时我们就要要求 ${\xi }_i$小，，即容忍度低。
\qquad 当C趋于无穷大时， ${\xi }_i$=0，软间隔问题就转换为硬间隔问题

创作挑战赛

新人创作奖励来咯，坚持创作打卡瓜分现金大奖