线性回归
单层神经网络-线性回归
线性回归是?个单层神经?络
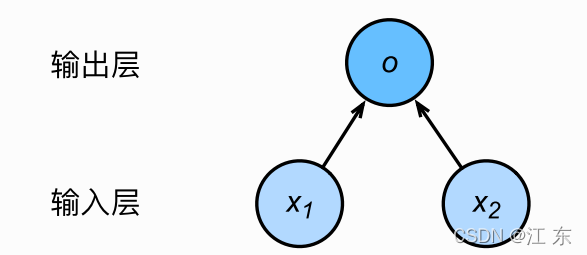
?输?分别为x1和x2,因此输?层的输?个数为2,输?个数也叫特征数或
特征向量维度,输出层的输出个数为1,输出层中的神经元和输?层中各个输?完全连
接,因此,这?的输出层?叫全连接层,即一个简单地线性回归。
?假设我们有三个预测数据:
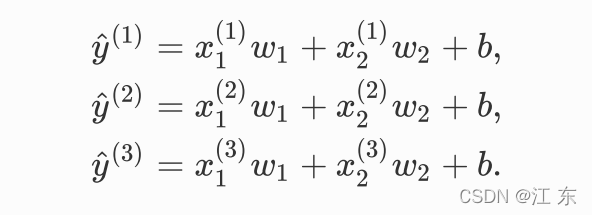
转化为矩阵运算:
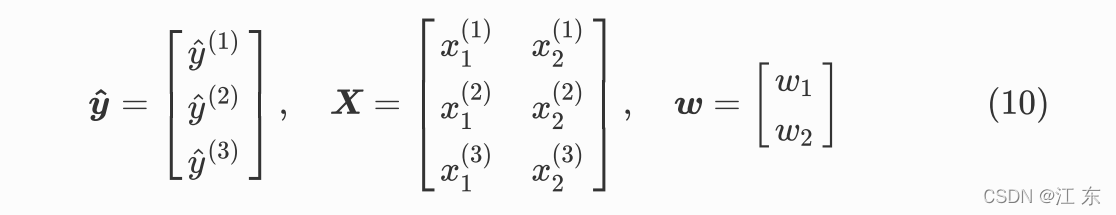
即
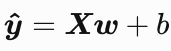
代码实现:
首先导入所需要的包:
import torch
import random
import numpy as np
from tqdm import tqdm
生成数据集:
num_input = 2
num_example = 1000 # 1000条样本
# 定义标准的参数
true_w = [2, -3.4]
true_b = 4.2
np.random.seed(2012)
features = torch.tensor(np.random.normal(0,1,(1000,2)))
# 构造标签
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] +true_b
labels += torch.from_numpy(np.random.normal(0, 0.01,size=labels.size()))
print(features,labels)
数据的读取:
def data_item(bach_size,features,labels):
num_examples = len(features)
indices = list(range(num_examples))
random.shuffle(indices) # 样本的读取顺序是随机的
for i in range(0, num_examples, bach_size):
j = torch.LongTensor(indices[i: min(i + bach_size,num_examples)]) # 最后?次可能不??个batch
yield features.index_select(0, j), labels.index_select(0, j)
随机初始化模型参数:
w = torch.tensor(np.random.normal(0, 0.01, (num_input, 1)),dtype=torch.double)
b = torch.zeros(1, dtype=torch.double)
w.requires_grad = True # 定义为可求梯度
b.requires_grad = True
定义线性回归函数,使? mm 函数(矩阵相乘):
def linear(x,w,b):
return torch.mm(x,w)+b
定义损失函数:
def loss(y_hat, y): # 本函数已保存在d2lzh_pytorch包中?便以后使?
return (y_hat - y.view(y_hat.size())) ** 2 / 2
定义优化函数:
def SGD(params, lr, batch_size): # 本函数已保存在d2lzh_pytorch包中?便以后使?
for param in params:
param.data -= lr * param.grad / batch_size # 修改的的param.data
训练模型:
lr = 0.03
bach_size = 30
net = linear
loss = loss
num_epochs = 5
for epoch in range(num_epochs):
for x,y in data_item(bach_size=bach_size,features=features,labels=labels):
los = loss(linear(x,w,b),y).sum()
los.backward()
SGD([w,b],lr=lr,batch_size=bach_size)
# print(b)
w.grad.zero_()
b.grad.zero_()
train_l = loss(net(features, w, b), labels)
print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))
print(true_w, '\n', w)
print(true_b, '\n', b)
喜欢文章可以点赞收藏,欢迎关注,如有错误请指正!
