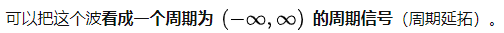这一节讲的太好了,看到GAMES202的第13讲回来继续深入学习一下信号处理。
采样理论
空间采样和时间采样
空间采样:照片上一格一格的像素。
时间采样:视频一秒只有固定的帧数。并不是记录了真实世界中连续的过程。
摩尔纹的产生
奇数行和奇数列都去掉再重新对在一起。
因为显示器是隔行扫描的,利用了人的视觉缺陷。
车轮错觉 Wagon Wheel Illusion
人眼在时间中的采样跟不上运动的速度
走样
信号变化的太快,以至于采样的速度跟不上它,产生走样。
采样与反走样(滤波)的顺序问题
先采样再滤波:不行
先滤波再采样:行
频域 Frequency Domain
傅里叶级数展开
任何一个周期函数都可以写成一系列正弦余弦函数的线性组合。
经过逆傅里叶变换,可以把傅里叶函数变回来原本的周期函数。
分解之后的函数:频率从低到高。
- 对低频函数采样,可以大概获得原来的函数长什么样。
- 对高频函数采样,恢复不出来原来的函数长什么样了。
- 结论就是对于什么频率的函数,就用什么样的频率去采样,这样才可以恢复出原来的函数来。
弹幕:不失真条件:大于奈奎斯特采样率。
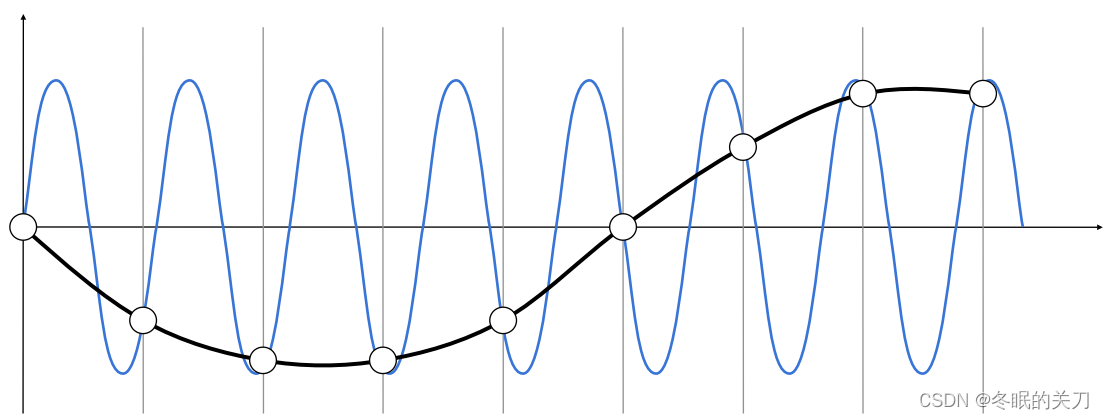
走样在信号里的定义,同样的采样方法在两种不同频率的函数信号下,得到的结果是相同的,我们无法区分它。
滤波 Filtering
把某个特定的频段抹掉,对应的信号如何发生变化。
对于傅里叶级数展开函数来说,就是把一部分的正余弦函数删除。
高通滤波

低通滤波

中通滤波

时域和频域
时域上的卷积等于频域上的乘积

两个时域信号的卷积最终可以展开成两两正弦信号的卷积的和。由于不同频率的正弦信号的卷积为0,所以最终只剩下相同频率的正弦信号的卷积。而卷积的结果就是频率不变,幅度相乘。
在频域里边就表现为直接相乘。
时域上的乘积等于频域上的卷积
有了这两条定理,就可以对一张图做卷积;也可以先把这张图傅里叶变换到频域上,把卷积滤波器也变到频域上,两者相乘,乘完之后得到频域的结果,再逆傅里叶变换,还原到时域上。
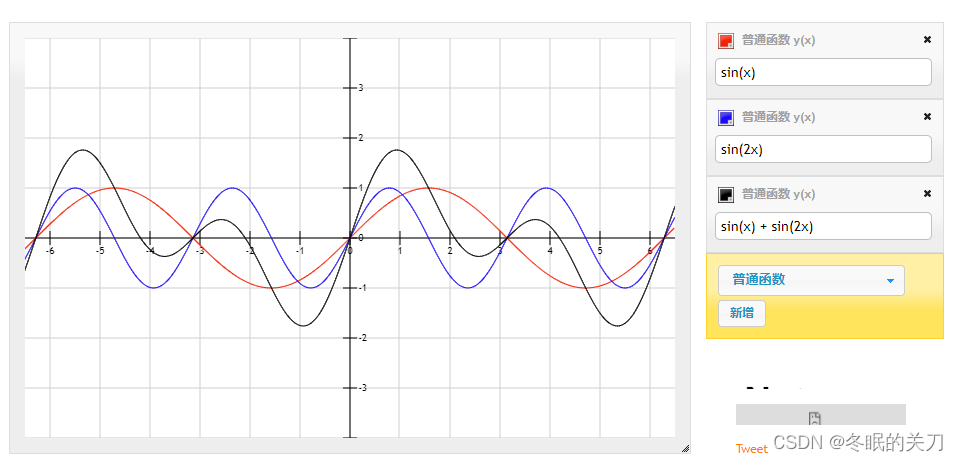
如图所见,sin(x) 频率 2PI 和sin(2x) 频率 PI是两个傅里叶频域曲线。
两个频域信号叠加,得到的结果频率和其中高频的曲线PI相同。
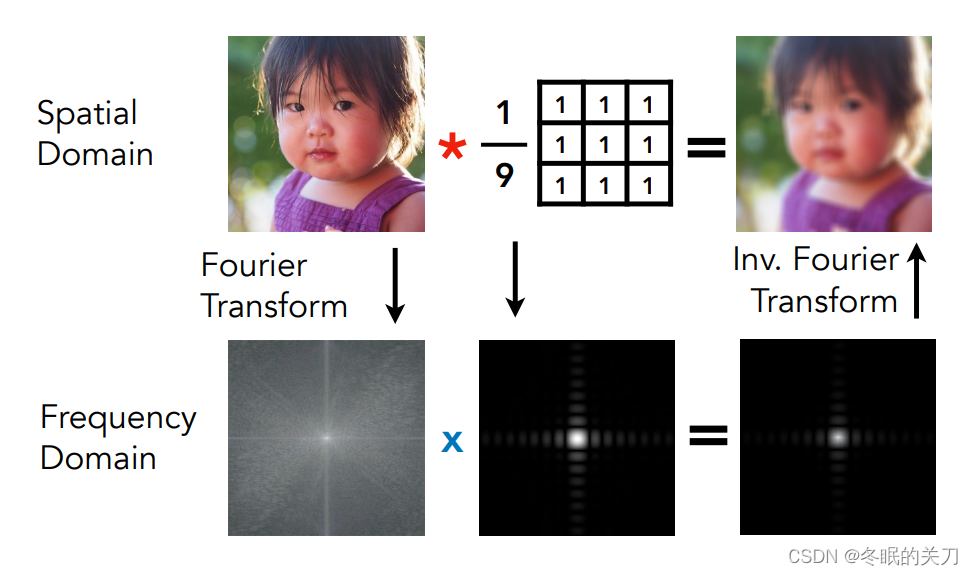
这就是一次利用本性质的滤波过程。
上面用到的滤波器是 Box Filter


BoxFilter 在时域上变大,那么它在频域上变小。
- 得到的结果更模糊
- 得到的结果更低频
- 弹幕:卷积核越大,保留的高频信息越少,低频信息越多,对应到频域图上,高频区域的亮度就降低了
- 验证方法:最小的BoxFilter就是1个像素的滤波器,会保留全部的信息,所以保留的高频信息是最多的。
采样
采样就是在重复频率或者频域上的内容
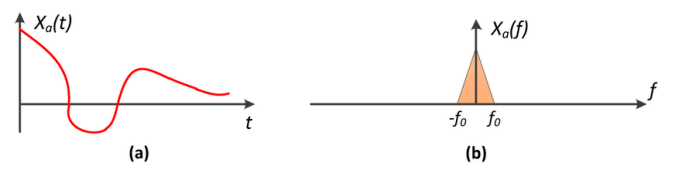
左为时域,右为频域。
目标:采样这个函数。
也就是用这个函数乘以另一个只在固定位置上有值的函数(冲激函数)。
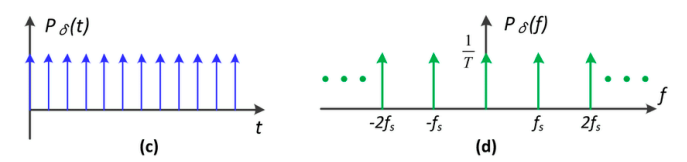
时域上的乘积等于频域上的卷积。得到下图
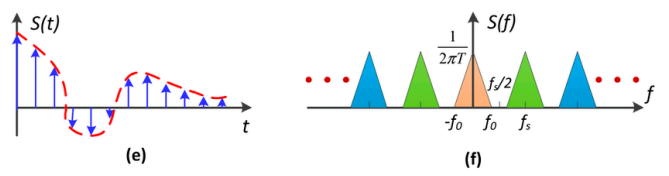
一个函数原本是连续的,现在变成了一系列离散的点。
其实就是把原始函数的频谱复制粘贴了很多。
所以采样就是在重复原始信号的频谱。
走样的原因
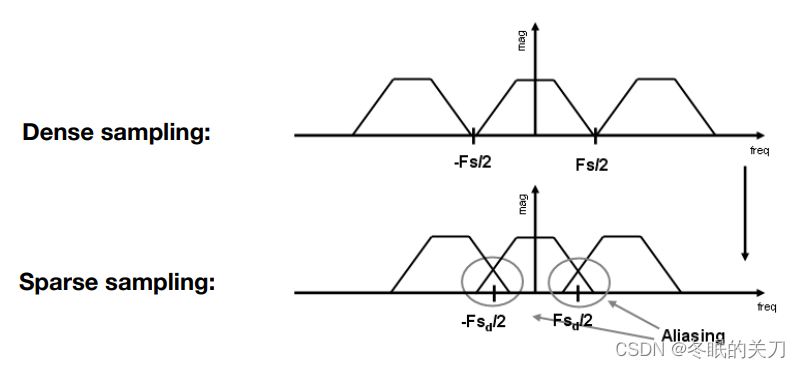
采样的不同间隔,会引起频谱以另外一个不同的间隔移动。
如果采样的不够快,意味着采样点之间的距离很大(时域上),频谱(频域)上的距离就会越小,就会使原本的信号频谱被复制粘贴后发生混合(混叠),就会产生走样的问题。
反走样
- 增加采样率。频谱搬移间隔大,就不容易混叠了。
- 先模糊再采样。低通滤波拿掉高频信息,然后再采样。
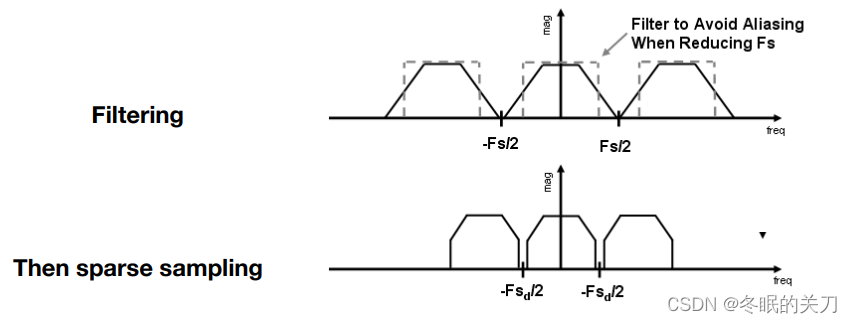
在不改变采样率的情况下,我们搬移的距离是固定的。
那么我们把原始信号砍掉,让它的频谱周期和搬移的距离相同,就能反走样。
《信号与系统》
分解复合波
目标:把复合波分解为一个个正弦波
整数倍正弦波之间是相互正交的,那么复合波和某个频率的正弦波做内积,如果不为零,那么这个复合波就有该频率的正弦波的成分,由此就可以分解出里面的成分。
去除复合波中的某些成分
如果我们想在一个复合波中去掉特定频率应该怎么做呢?卷积( 频率滤波器的作用)
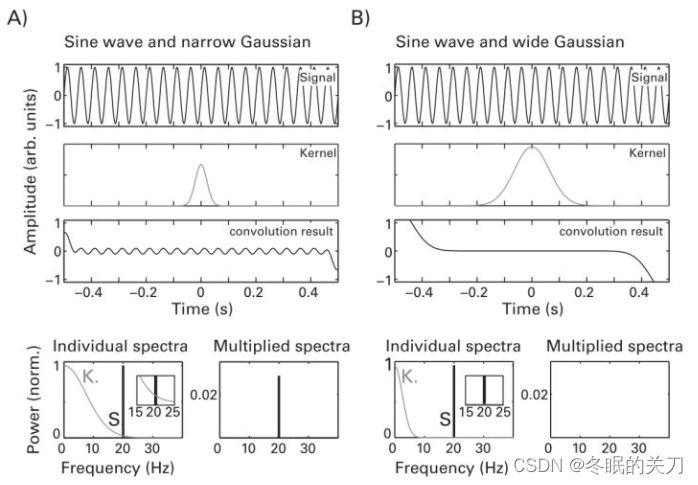
正弦波(20hz)和窄高斯的卷积结果简单地抑制了正弦波的振幅,而宽高斯卷积的结果则使正弦波消失
非周期波的分解