降维(Dimensionality Reduction)
视频参考:【机器学习】【白板推导系列】【合集 1~33】_哔哩哔哩_bilibili
笔记参考:降维 · 语雀 (yuque.com)
PCA原理详解:主成分分析(PCA)原理详解 - 知乎 (zhihu.com)
PCA数学原理解释:CodingLabs - PCA的数学原理
SVD奇异值分解:?奇异值分解(SVD) - 知乎 (zhihu.com)
过拟合
- 增加数据
- 正则化
- 降维
- 直接降维(特征选择)
- 线性降维(PCA、MDS)
- 非线性降维(流形学习(Isomap、LLE))
维度灾难(数据稀疏性):几何角度

对于高维空间而言, 维度越高,球形体的体积越小
样本均值 & 样本协方差矩阵

- ?
表示存在N个数据,其中每个数据维度为P维
表示为中心矩阵, 其中
主成分分析(PCA)
最大的投影方向, 叫做主成分
一个中心:原始特征空间的重构
两个基本点:
- 最大投影方差
- 最小重构距离
最大投影方差? --> 寻找投影后距离范围最大的向量
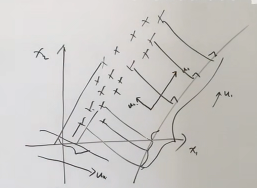


?一、计算两个向量之间的投影值? =>?表示向量的投影
二、计算方差最小值J,
其中?
最小重构代价 --> 降低特征维度损失最小


?一、对于向量重新选择向量基, 将维度由p维 降到 q维
二、计算最小重构代价,转换为最优化问题, 其中求解
最小值
SVD角度看PCA
方差矩阵S,?,
, 方差矩阵S是对称矩阵, 对方差矩阵S进行特征分解就是奇异值分解
奇异值SVD分解:奇异值分解(SVD) - 知乎 (zhihu.com)
SVD的作用就相当于是一个坐标系变换的过程,从一个不标准的n维坐标系,转换为一个标准的k维坐标系,并且使这个数据集中的点,到这个新坐标系的欧式距离为最小值(也就是这些点在这个新坐标系中的投影方差最大化),其实就是一个最小二乘的过程。
进一步,如何使数据在新坐标系中的投影最大化呢,那么我们就需要让这个新坐标系中的基尽可能的不相关,我们可以用协方差来衡量这种相关性。A^T·A中计算的便是n×n的协方差矩阵,每一个值代表着原来的n个特征之间的相关性。当对这个协方差矩阵进行特征分解之后,我们可以得到奇异值和右奇异矩阵,而这个右奇异矩阵则是一个新的坐标系,奇异值则对应这个新坐标系中每个基对于整体数据的影响大小,我们这时便可以提取奇异值最大的k个基,作为新的坐标,这便是PCA的原理。

使用SVD奇异值分解, 直接获取主成分分析 or 主坐标分析
X表示数据, HX表示中心化数据, 对HX进行奇异值分解得到
概率角度P-PCA
完全没有听懂

?
