[人工智能]10.2注意力汇聚

原文链接

下面为学习记录：

1964年提出的Nadaraya-Watson核回归模型 是一个简单但完整的例子，可以用于演示具有注意力机制的机器学习。

1. 生成数据集

简单起见，考虑下面这个回归问题： 给定的成对的“输入－输出”数据集 { ( x 1 , y 1 ) , … , ( x n , y n ) } \{(x_1, y_1), \ldots, (x_n, y_n)\} {(x1?,y1?),…,(xn?,yn?)}，

如何学习注意力层的 $f$函数，来预测任意新输入$x$的输出
$\hat{y}=f(x)$？

根据下面的非线性函数生成一个人工数据集， 其中加入的噪声项为：
$y_i=2\sin (x_i)+x_i^{0.8}+?,$

其中$?$服从均值为0 和标准差为0.5 的正态分布。

我们生成了50个训练样本和50个测试样本。

为了更好地可视化之后的注意力模式，我们将训练样本进行排序。

2. 平均池化方式的输出

我们先使用最简单的估计器来解决回归问题： 基于平均汇聚来计算所有训练样本输出值的平均值：

$$f(x)=\frac{1}{n}\sum _{i=1}^n{y}_i,$$

如下图所示，这个估计器确实不够聪明： 真实函数（“Truth”）和预测函数（“Pred”）相差很大。

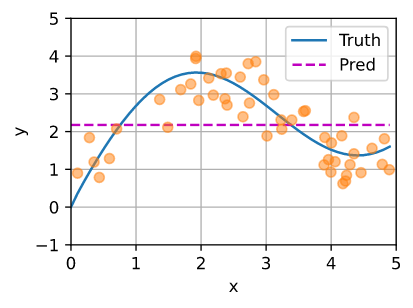
3. 核回归方法的注意力函数

显然，平均汇聚忽略了输入$x_i$。

于是Nadaraya [Nadaraya, 1964]和 Watson [Watson, 1964]提出了一个更好的想法， 根据输入的位置对输出
$y_i$进行加权：

$$f(x)=\sum _{i=1}^n\frac{K(x?x_i)}{{\sum }_{j=1}^{n}K(x?x_j)}{y}_i,$$

其中$K$是核（kernel）。
公式所描述的估计器被称为 Nadaraya-Watson核回归（Nadaraya-Watson kernel regression）。

3.1 无参数的核回归方法：

这里我们不会深入讨论核函数的细节， 但受此启发， 我们可以从 图10.1.3中的注意力机制框架的角度 重写 (10.2.3)， 成为一个更加通用的注意力汇聚（attention pooling）公式：
$$f(x)=\sum _{i=1}^n\alpha (x,x_i)y_i,$$

其中是$x$查询，$(x_i,y_i)$是键值对。

注意力层的输出是预测值$y_i$的加权平均。

将查询$x$和键$x_i$之间的关系建模为注意力权重（attention weight）$\alpha (x,x_i)$，

这个权重将被分配给每一个对应值$y_i$。

对于任何查询，模型在所有键值对注意力权重都是一个有效的概率分布： 它们是非负的，并且总和为1。

为了更好地理解注意力汇聚， 我们考虑一个高斯核（Gaussian kernel），其定义为：
$$K(u)=\frac{1}{\sqrt{2\pi }}\exp (?\frac{u^2}{2}).$$

将高斯核代入, 可以得到：

$$\begin{array}{rl}f(x)& =\sum _{i=1}^n\alpha (x,x_i)y_i\\ & =\sum _{i=1}^n\frac{\exp \left(?\frac{1}{2}(x?x_i{)}^2\right)}{{\sum }_{j=1}^n\exp \left(?\frac{1}{2}(x?x_j{)}^2\right)}{y}_i\\ & =\sum _{i=1}^n\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left(?\frac{1}{2}(x?x_i{)}^2\right)y_i.\end{array}$$

如果一个键$x_i$越是接近给定的查询$x$， 那么分配给这个键对应值 $y_i$的注意力权重就会越大， 也就“获得了更多的注意力”。

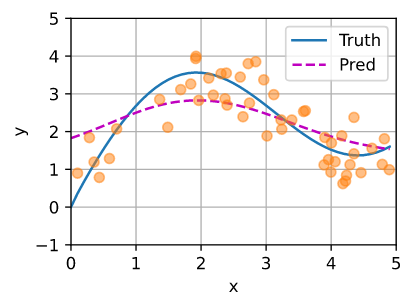
值得注意的是，Nadaraya-Watson核回归是一个非参数模型。 因此， 非参数的注意力汇聚（nonparametric attention pooling）模型。 接下来，我们将基于这个非参数的注意力汇聚模型来绘制预测结果。

你会发现新的模型预测线是平滑的，并且比平均汇聚的预测更接近真实。

3.2 有参数的核回归方法：

非参数的Nadaraya-Watson核回归具有一致性（consistency）的优点： 如果有足够的数据，此模型会收敛到最优结果。 尽管如此，我们还是可以轻松地将可学习的参数集成到注意力汇聚中。

例如: 在下面的查询$x$和键$x_i$ 之间的距离乘以可学习参数$w$：

$$\begin{array}{rl}f(x)& =\sum _{i=1}^n\alpha (x,x_i)y_i\\ & =\sum _{i=1}^n\frac{\exp \left(?\frac{1}{2}((x?x_i)w{)}^2\right)}{{\sum }_{j=1}^n\exp \left(?\frac{1}{2}((x?x_j)w{)}^2\right)}{y}_i\\ & =\sum _{i=1}^n\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left(?\frac{1}{2}((x?x_i)w{)}^2\right)y_i.\end{array}$$

阅读世界，共赴山海

423全民读书节，邀你共读