1 plot(Y)
plot(Y) 创建 Y 中数据对每个值索引的二维线图。
如果 Y 是向量,x 轴的刻度范围是从 1 至 length(Y),此种情况示例代码如下:
t=1:0.1:10;
y=sin(t);
plot(y);
运行结果如下图所示:
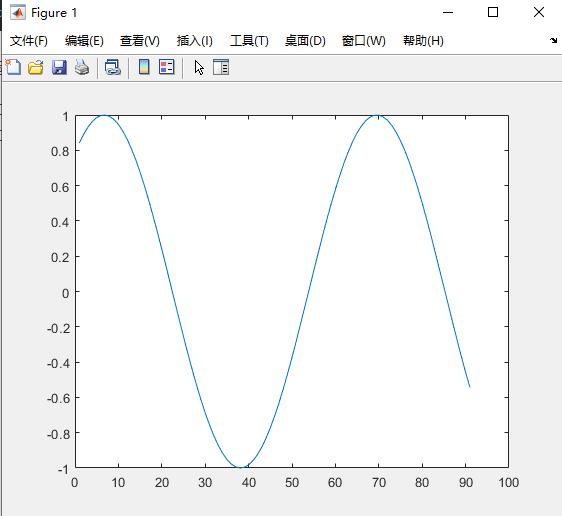
注意:上面中的横坐范围并不是[1,10] 而是 [1,91],[1,91]正是向量y的索引,如下图所示:
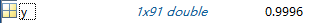
如果 Y 是矩阵,则 plot 函数绘制 Y 中各列对其行号的图。x 轴的刻度范围是从 1 到 Y 的行数。此种情况示例代码如下:
Y=[1 2 3;4 5 6;7 8 9;10 11 12];
plot(Y);
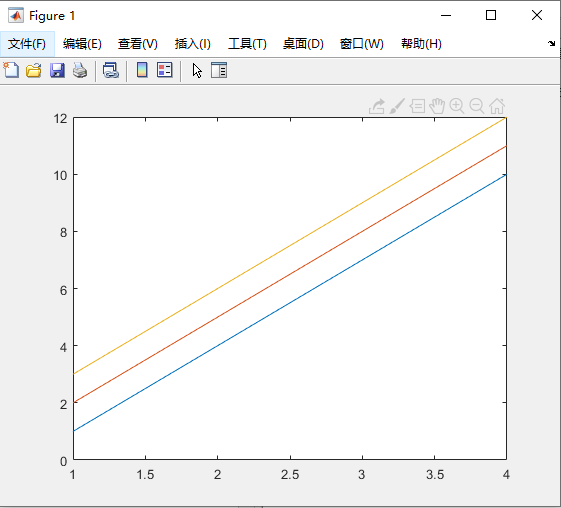
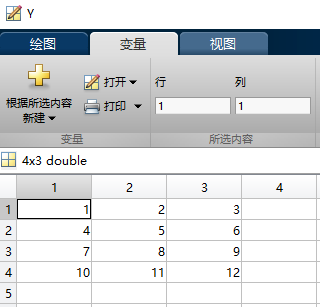
从上面两幅幅可以看出,图中的蓝线便是矩阵的第1列,图中的红线便是矩阵的第2列,图中的黄线便是矩阵的第3列。矩阵有几列便有几条线。x 轴的刻度范围是从 1 到 Y 的行数。
如果 Y 是复数,则 plot 函数绘制 Y 的虚部对 Y 的实部的图(即虚部为y轴,实部为x轴),使得 plot(Y) 等效于 plot(real(Y),imag(Y))。此种情况示例代码如下:
x=1:1:100;
y=2:2:200;
z=x+y.*1i;
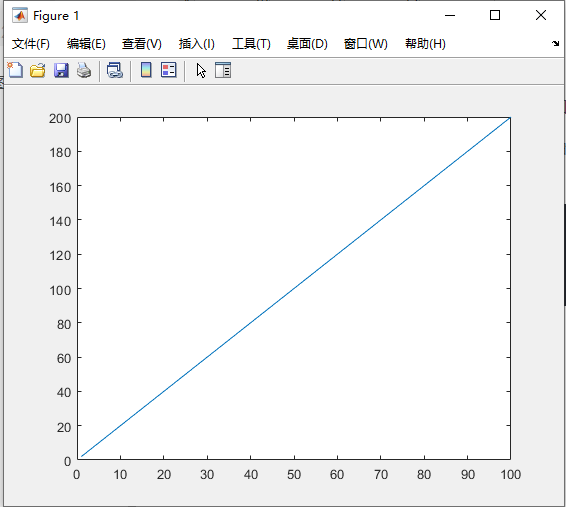
plot(z);
运行结果如下图所示:
2 plot(X,Y)
plot(X,Y) 创建 Y 中数据对 X 中对应值的二维线图。
如果 X 和 Y 都是向量,则它们的长度必须相同。plot 函数绘制 Y 对 X 的图,即X为横轴,Y为纵轴。此种情况示例代码如下:
x=0:0.1:10;
y=sin(x)+2;
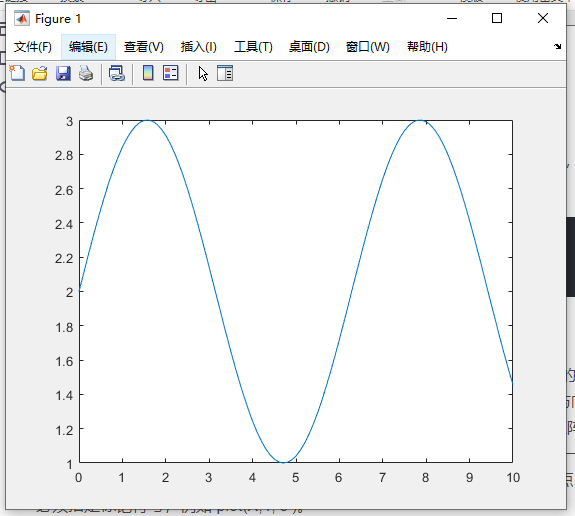
plot(x,y);
运行结果如下:
如果 X 和 Y 均为矩阵,则它们的大小必须相同。plot 函数绘制 Y 的列对 X 的列的图。即X和Y的每一列绘制成一条曲线,并且以X的列为x轴,Y的列为y轴。此种情况示例代码如下:
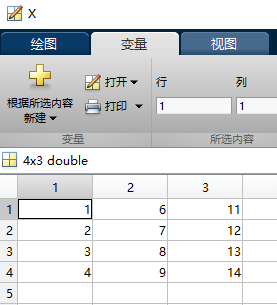
X=[1 6 11;2 7 12;3 8 13;4 9 14];
Y=[2 18 44;4 21 48;6 24 52;8 27 56];
plot(X,Y);
运行结果如下图所示:
 ??
??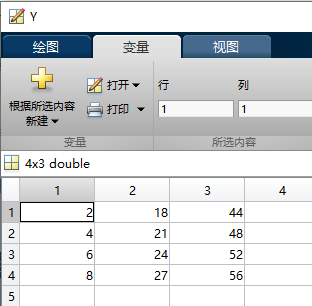
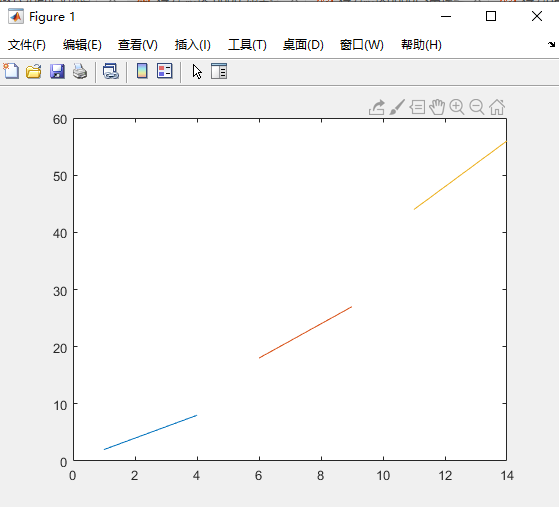
图中蓝色的线是X矩阵和Y矩阵第1列元素形成的曲线;红色的线是X矩阵和Y矩阵第2列元素形成的曲线;橙色的线是X矩阵和Y矩阵第3列元素形成的曲线。
如果 X 或 Y 中的一个是向量而另一个是矩阵,则矩阵的各维中必须有一维与向量的长度相等。如果矩阵的行数等于向量长度,则 plot 函数绘制矩阵中的每一列对向量的图。如果矩阵的列数等于向量长度,则该函数绘制矩阵中的每一行对向量的图。如果矩阵为方阵,则该函数绘制每一列对向量的图。此种情况示例代码如下:
x=0:0.1:10;
y=[sin(x)+2;cos(x)+1];
plot(x,y);
运行结果如下:
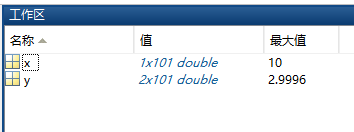
从运行结果可以看出,y矩阵的列数等于向量x的长度,所以第一条曲线就是矩阵y的一行,并且以向量x为横坐标。
如果 X 或 Y 之一为标量,而另一个为标量或向量,则 plot 函数会绘制离散点。但是,要查看这些点,您必须指定标记符号,例如 plot(X,Y,‘o’)。此种情况示例代码如下:
x=3;
y=0:1:10;
plot(x,y,'o')
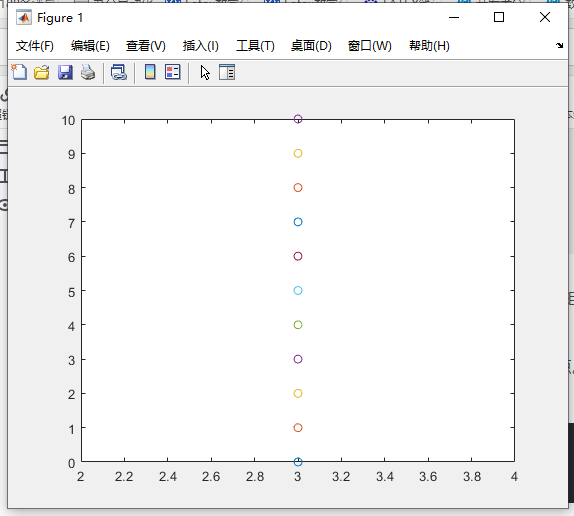
3 plot(___,Name,Value)
此格式用于设置线条的格式,比如线条的颜色、线型、点标等。
具体的使用方法为:指定可选的、以逗号分隔的 Name,Value 对组参数。Name 为参数名称,Value 为对应的值。Name 必须放在引号中。您可采用任意顺序指定多个名称-值对组参数,如 Name1,Value1,…,NameN,ValueN 所示。
使用示例如下:
x=0:0.5:20;
y=sin(x);
plot(x,y,'color','[0 0 1]','Marker','+');
运行结果:
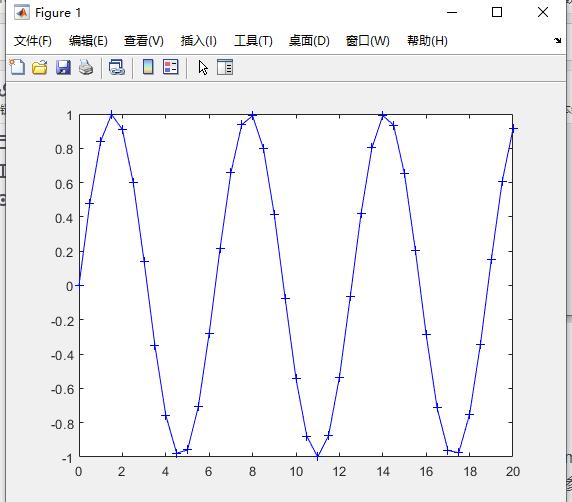
这里可设置的线条格式有如下这些:
‘Color’ —线条颜色
‘LineStyle’ — 线型
‘Marker’—标记符号
‘LineWidth’—线条宽度
‘MarkerIndices’—要显示标记的数据点的索引
‘MarkerEdgeColor’—标记轮廓颜色
‘MarkerFaceColor’—标记填充颜色
‘MarkerSize’—标记大小
DatetimeTickFormat’—datetime 刻度标签的格式
‘DurationTickFormat’—duration 刻度标签的格式
常用的是前三个,即线条颜色、线型和标记符号,这三个的一般可选参数如下:
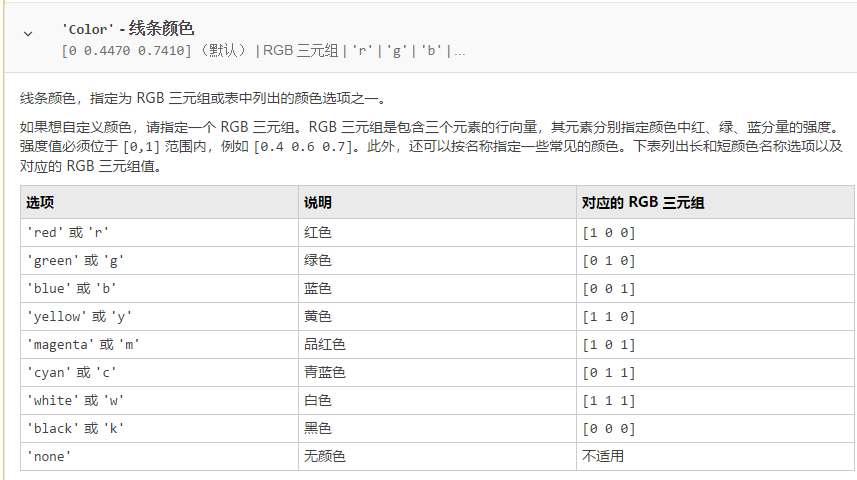
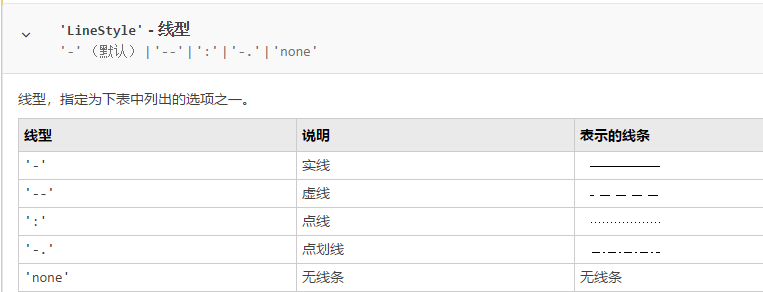
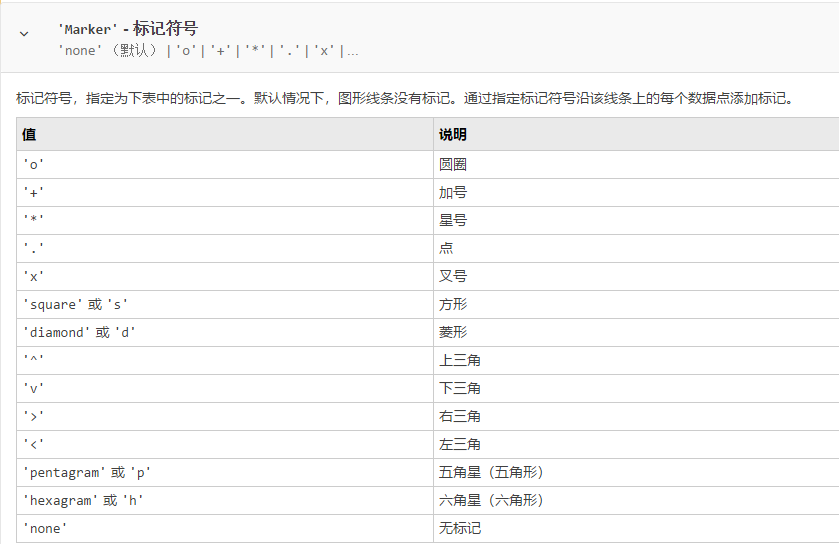
其它格式的可选参数大家去查阅MATLAB的帮助文档吧。
4 坐标轴标注和图形标题
对坐标轴进行标注和给图形加标题的函数主要有xlabel、ylabel zlabel和title等。它们的调用格式基本相同,使用也很简单,看一个实例就知道怎么用了。
x=1:0.1*pi:2*pi;
y=sin(x);
plot(x,y);
xlabel('x(0-2\pi)','fontweight','bold');
ylabel('y=sin(x)','fontweight','bold');
title('正弦函数','fontsize',12,'fontweight','bold','fontname','宋体');
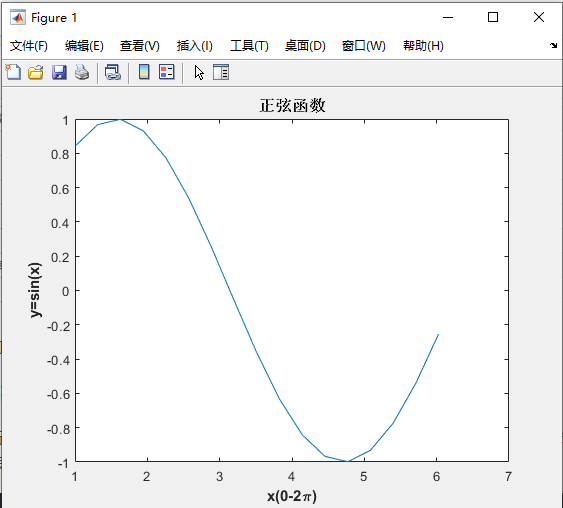
更多关于它们的格式属性设置可以去查阅MATLAB的帮助文档。
5图例标注
我们经常会遇到在一张图中绘制多条曲线的情况,这时我们可以使用函数legend()为曲线添加图例以例区别它们。
x = linspace(0,2*pi);
y1 = sin(x);
y2 = cos(x);
plot(x,y1,x,y2);
legend('sin(x)','cos(x)');
运行结果如下:
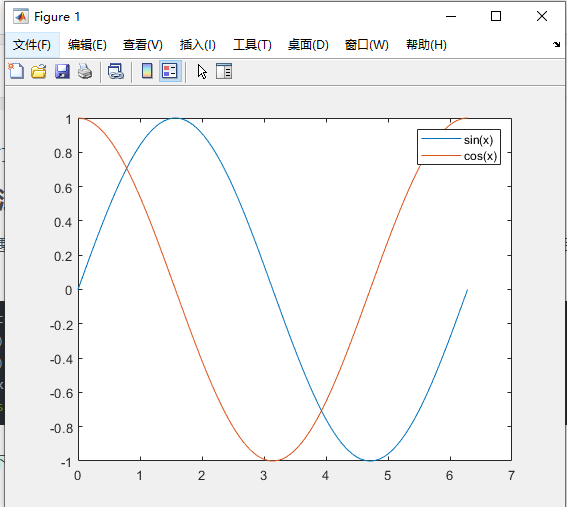
函数plot()和函数legend()的使用其实是非常灵活的,比如下面的代码:
x = linspace(0,2*pi);
y1 = cos(x);
plot(x,y1,'DisplayName','cos(x)')
hold on
y2 = cos(2*x);
plot(x,y2,'DisplayName','cos(2x)')
hold off
legend
运行结果如下图:
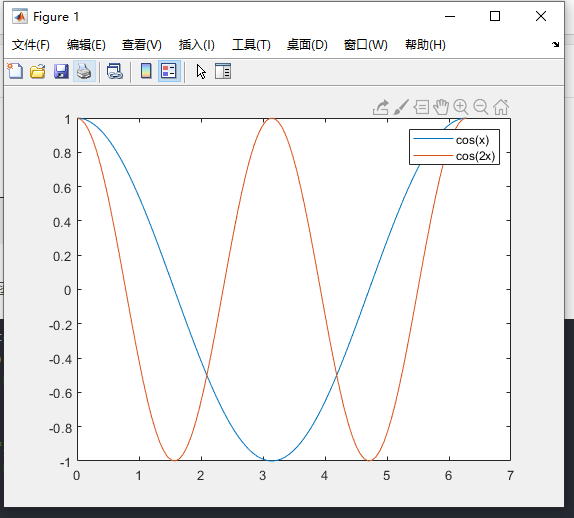
6 目前MATLAB的文本已支持Latex公式输入
如下面的代码:
x = 0:0.01:1;
y1= x.^(1/2.2);
y2 =x.^(2.2);
plot(x,y1,x,y2);
xlabel('V_{in}');
ylabel('V_{out}');
legend('\gamma=1/2.2','\gamma=2.2');
运行结果如下:
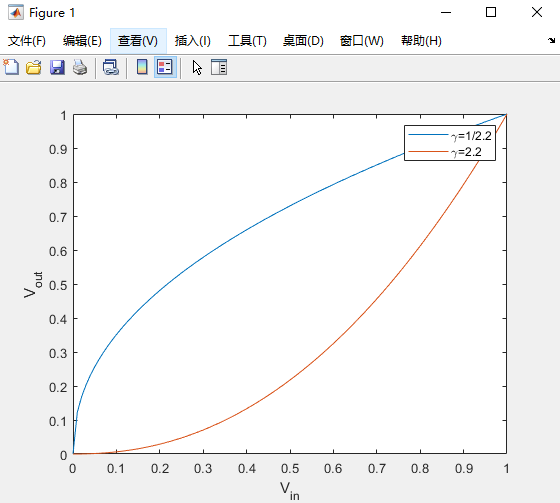
从运行结果中我们可以看出,下标都放置于正确位置了。“gamma”也被转义成了“γ”
