Step1:库函数导入
# 基础函数库
import numpy as np
import pandas as pd
# 绘图函数库
import matplotlib.pyplot as plt
import seaborn as sns
鸢尾花数据集(iris)一共包含5个变量,其中4个特征变量,1个目标分类变量。共有150个样本,目标变量为花的类别,其都属于鸢尾属下的三个亚属,分别是山鸢尾 (Iris-setosa),变色鸢尾(Iris-versicolor) 和 维吉尼亚鸢尾(Iris-virginica)。包含的三种鸢尾花的四个特征,分别是花萼长度(cm)、花萼宽度(cm)、花瓣长度(cm)、花瓣宽度(cm),这些形态特征在过去被用来识别物种。
| 变量 | 描述 |
|---|---|
| sepal length | 花萼长度(cm) |
| sepal width | 花萼宽度(cm) |
| petal length | 花瓣长度(cm) |
| petal width | 花瓣宽度(cm) |
| target | 鸢尾的三个亚属类别,‘setosa’(0), ‘versicolor’(1), ‘virginica’(2) |
Step2:数据读取/载入
# 利用 sklearn 中自带的 iris 数据作为数据载入,并利用Pandas转化为DataFrame格式
from sklearn.datasets import load_iris
data = load_iris() # 得到数据特征
iris_target = data.target # 得到数据对应的标签
iris_features = pd.DataFrame(data=data.data, columns=data.feature_names) # 利用Pandas转化为DataFrame格式
Step3: 数据信息简单查看
## 利用.info()查看数据的整体信息
iris_features.info()
<class ‘pandas.core.frame.DataFrame’>
RangeIndex: 150 entries, 0 to 149
Data columns (total 4 columns):
Column Non-Null Count Dtype
0 sepal length (cm) 150 non-null float64
1 sepal width (cm) 150 non-null float64
2 petal length (cm) 150 non-null float64
3 petal width (cm) 150 non-null float64
dtypes: float64(4)
memory usage: 4.8 KB
## 进行简单的数据查看,我们可以利用 .head() 头部.tail()尾部
iris_features.head()
iris_features.tail()
## 其对应的类别标签为,其中0,1,2分别代表'setosa', 'versicolor', 'virginica'三种不同花的类别。
iris_target
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])
## 利用value_counts函数查看每个类别数量
pd.Series(iris_target).value_counts()
2 50
1 50
0 50
dtype: int64
## 对于特征进行一些统计描述
iris_features.describe()

从统计描述中我们可以看到不同数值特征的变化范围。
Step4:可视化描述
# 合并标签和特征信息
iris_all = iris_features.copy() ##进行浅拷贝,防止对于原始数据的修改
iris_all['target'] = iris_target
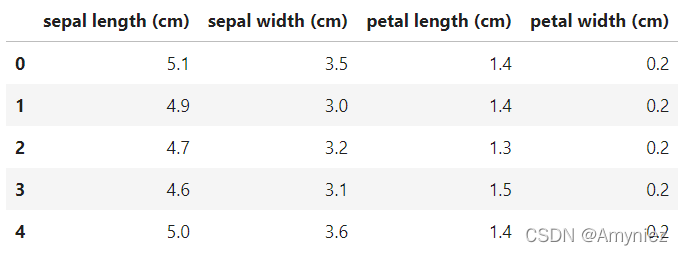
# 特征与标签组合的散点可视化
sns.pairplot(data=iris_all,diag_kind='hist', hue= 'target')
plt.show()
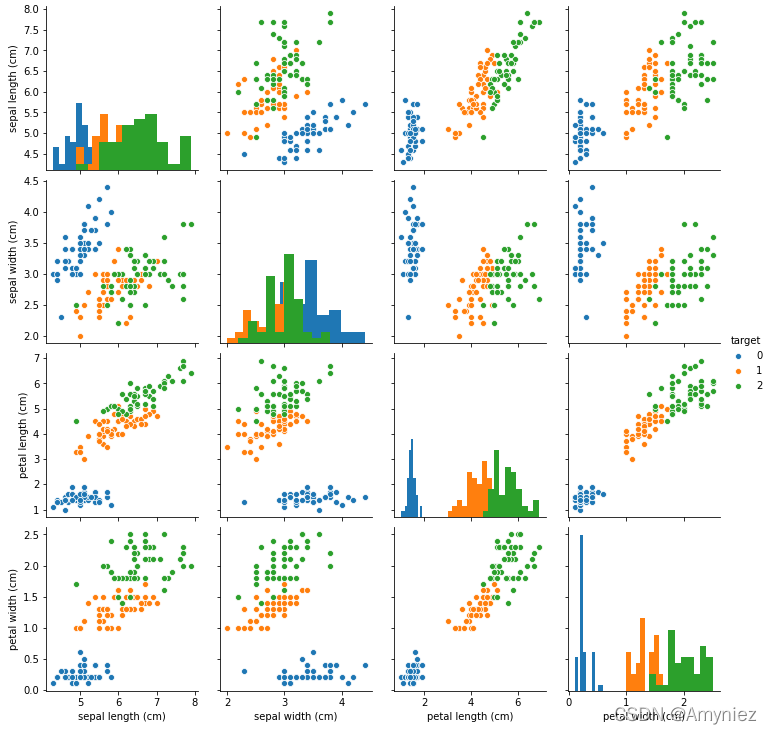
绘制箱型图:
- 箱形图五要素 : .
- 1、中位数: 即二分之一分位数。所以计算的方法就是将一组数据(此处中位数,特别指是从大到小排列的有序序列)平均分成两份,取中间这个数。如果原始序列长度n是奇数,那么中位数所在位置是(n+1)/2;如果原始序列长度n是偶数,那么中位数所在位置是n/2,n/2+1,中位数的值等于这两个位置的数的算数平均数。
- 2、上四分位数Q1: 强调一下,四分位数的求法,是将序列平均分成四份。具体的计算目前有(n+1)/4与(n-1)/4两种,一般使用(n+1)/4。
例如: 有序序列一个test = c(1,2,3,4,5,6,7,8),通过summary(test)来获取test这个序列的中位数,上四分位数,下四分位数以及算数平均值。首先序列长度n=8,(1+n)/4=2.25,说明上四分位数在第2.25个位置数,那么第2.25个数就是第二个数0.25+第三个数0.75,即20.25+3*0.75=0.5+2.25=2.75。 - 3、下四分位数Q3: 这个下四分位数所在位置计算方法同上,只不过是(1+n)/43=6.75,这个是个介于第六个位置与第七个位置之间的地方。对应的具体的值是0.756+0.25*7=6.25。
- 4、内限: 上面的T形线段所延伸到的极远处,是Q3+1.5IQR(其中,IQR=Q3-Q1)与剔除异常值后的极大值两者取最小,下面的T形线段所延伸到的极远处,是Q1-1.5IQR与剔除异常值后的极小值两者取最大。
(1,6,2,7,4,2,3,3,8,25,30)
IQR=Q3-Q1=7.5-2.5=5
上内限=Q3+1.5IQR=7.5+1.55=15,与剔除两个异常址30,25后的极大值8,两者取最小值,所以上内限就是8
下内限=Q1-1.5IQR=2.5-1.55=-5,与剔除两个异常址30,25后的极小值1,两者取最大值,所以下内限就是1 - 5、外限: 外限与内限的计算方法相同,唯一的区别就在与:上面的T形线段所延伸到的极远处,是Q3+3IQR(其中,IQR=Q3-Q1)与剔除异常值后的极大值两者取最小,下面的T形线段所延伸到的极远处,是Q1-3IQR与剔除异常值后的极小值两者取最大。
for col in iris_features.columns:
sns.boxplot(x='target', y=col, saturation=0.5,palette='pastel', data=iris_all)
plt.title(col)
plt.show()

箱形图最大的优点就是: 不受异常值的影响,可以以一种相对稳定的方式描述数据的离散分布情况。
利用箱型图我们也可以得到不同类别在不同特征上的分布差异情况。
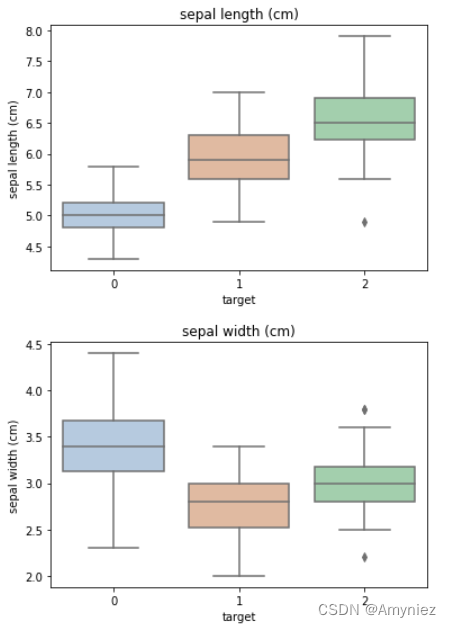
# 选取其前三个特征绘制三维散点图
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=(10,8))
ax = fig.add_subplot(111, projection='3d')
iris_all_class0 = iris_all[iris_all['target']==0].values
iris_all_class1 = iris_all[iris_all['target']==1].values
iris_all_class2 = iris_all[iris_all['target']==2].values
# 'setosa'(0), 'versicolor'(1), 'virginica'(2)
ax.scatter(iris_all_class0[:,0], iris_all_class0[:,1], iris_all_class0[:,2],label='setosa')
ax.scatter(iris_all_class1[:,0], iris_all_class1[:,1], iris_all_class1[:,2],label='versicolor')
ax.scatter(iris_all_class2[:,0], iris_all_class2[:,1], iris_all_class2[:,2],label='virginica')
plt.legend()
plt.show()
Step5:利用 逻辑回归模型 在二分类上 进行训练和预测
## 为了正确评估模型性能,将数据划分为训练集和测试集,并在训练集上训练模型,在测试集上验证模型性能。
from sklearn.model_selection import train_test_split
## 选择其类别为0和1的样本 (不包括类别为2的样本)
iris_features_part = iris_features.iloc[:100]
iris_target_part = iris_target[:100]
## 测试集大小为20%, 80%/20%分
x_train, x_test, y_train, y_test = train_test_split(iris_features_part, iris_target_part, test_size = 0.2, random_state = 2020)
## 从sklearn中导入逻辑回归模型
from sklearn.linear_model import LogisticRegression
## 定义 逻辑回归模型
clf = LogisticRegression(random_state=0, solver='lbfgs')
# 在训练集上训练逻辑回归模型
clf.fit(x_train, y_train)
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, l1_ratio=None, max_iter=100,
multi_class=‘auto’, n_jobs=None, penalty=‘l2’,
random_state=0, solver=‘lbfgs’, tol=0.0001, verbose=0,
warm_start=False)
## 查看其对应的w
print('the weight of Logistic Regression:',clf.coef_)
## 查看其对应的w0
print('the intercept(w0) of Logistic Regression:',clf.intercept_)
the weight of Logistic Regression: [[ 0.45181973 -0.81743611 2.14470304 0.89838607]]
the intercept(w0) of Logistic Regression: [-6.53367714]
## 在训练集和测试集上分布利用训练好的模型进行预测
train_predict = clf.predict(x_train)
test_predict = clf.predict(x_test)
from sklearn import metrics
## 利用accuracy(准确度)【预测正确的样本数目占总预测样本数目的比例】评估模型效果
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_train,train_predict))
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_test,test_predict))
## 查看混淆矩阵 (预测值和真实值的各类情况统计矩阵)
confusion_matrix_result = metrics.confusion_matrix(test_predict,y_test)
print('The confusion matrix result:\n',confusion_matrix_result)
# 利用热力图对于结果进行可视化
plt.figure(figsize=(8, 6))
sns.heatmap(confusion_matrix_result, annot=True, cmap='Blues')
plt.xlabel('Predicted labels')
plt.ylabel('True labels')
plt.show()
The accuracy of the Logistic Regression is: 1.0
The accuracy of the Logistic Regression is: 1.0
The confusion matrix result:
[[ 9 0]
[ 0 11]]
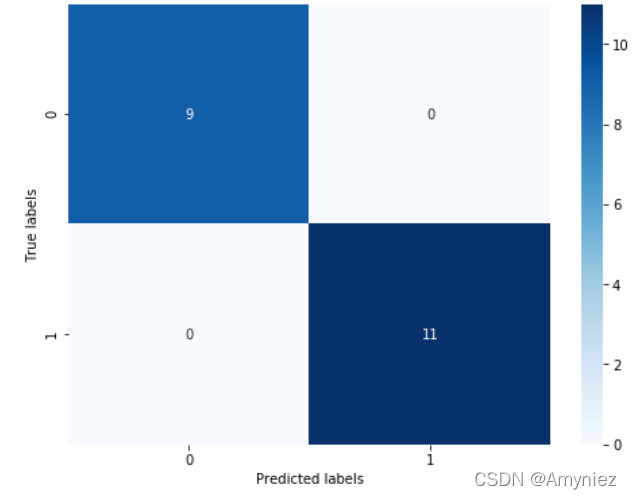
可以发现其准确度为1,代表所有的样本都预测正确了。
Step6:利用 逻辑回归模型 在三分类(多分类)上 进行训练和预测
## 测试集大小为20%, 80%/20%分
x_train, x_test, y_train, y_test = train_test_split(iris_features, iris_target, test_size = 0.2, random_state = 2020)
## 定义 逻辑回归模型
clf = LogisticRegression(random_state=0, solver='lbfgs')
# 在训练集上训练逻辑回归模型
clf.fit(x_train, y_train)
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True,
intercept_scaling=1, l1_ratio=None, max_iter=100,
multi_class=‘auto’, n_jobs=None, penalty=‘l2’,
random_state=0, solver=‘lbfgs’, tol=0.0001, verbose=0,
warm_start=False)
## 查看其对应的w
print('the weight of Logistic Regression:\n',clf.coef_)
## 查看其对应的w0
print('the intercept(w0) of Logistic Regression:\n',clf.intercept_)
## 由于这个是3分类,所有我们这里得到了三个逻辑回归模型的参数,其三个逻辑回归组合起来即可实现三分类。
the weight of Logistic Regression:
[[-0.45928925 0.83069886 -2.26606531 -0.9974398 ]
[ 0.33117319 -0.72863423 -0.06841147 -0.9871103 ]
[ 0.12811606 -0.10206463 2.33447679 1.9845501 ]]
the intercept(w0) of Logistic Regression:
[ 9.43880677 3.93047364 -13.36928041]
## 在训练集和测试集上分布利用训练好的模型进行预测
train_predict = clf.predict(x_train)
test_predict = clf.predict(x_test)
## 由于逻辑回归模型是概率预测模型(前文介绍的 p = p(y=1|x,\theta)),所有我们可以利用 predict_proba 函数预测其概率
train_predict_proba = clf.predict_proba(x_train)
test_predict_proba = clf.predict_proba(x_test)
print('The test predict Probability of each class:\n',test_predict_proba)
## 其中第一列代表预测为0类的概率,第二列代表预测为1类的概率,第三列代表预测为2类的概率。
## 利用accuracy(准确度)【预测正确的样本数目占总预测样本数目的比例】评估模型效果
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_train,train_predict))
print('The accuracy of the Logistic Regression is:',metrics.accuracy_score(y_test,test_predict))
The test predict Probability of each class:
[[1.03461734e-05 2.33279475e-02 9.76661706e-01]
[9.69926591e-01 3.00732875e-02 1.21676996e-07]
[2.09992547e-02 8.69156617e-01 1.09844128e-01]
[3.61934870e-03 7.91979966e-01 2.04400685e-01]
[7.90943202e-03 8.00605300e-01 1.91485268e-01]
[7.30034960e-04 6.60508053e-01 3.38761912e-01]
[1.68614209e-04 1.86322045e-01 8.13509341e-01]
[1.06915332e-01 8.90815532e-01 2.26913667e-03]
[9.46928070e-01 5.30707294e-02 1.20016057e-06]
[9.62346385e-01 3.76532233e-02 3.91897289e-07]
[1.19533384e-04 1.38823468e-01 8.61056998e-01]
[8.78881883e-03 6.97207361e-01 2.94003820e-01]
[9.73938143e-01 2.60617346e-02 1.22613836e-07]
[1.78434056e-03 4.79518177e-01 5.18697482e-01]
[5.56924342e-04 2.46776841e-01 7.52666235e-01]
[9.83549842e-01 1.64500670e-02 9.13617258e-08]
[1.65201477e-02 9.54672749e-01 2.88071038e-02]
[8.99853708e-03 7.82707576e-01 2.08293887e-01]
[2.98015025e-05 5.45900066e-02 9.45380192e-01]
[9.35695863e-01 6.43039513e-02 1.85301359e-07]
[9.80621190e-01 1.93787400e-02 7.00125246e-08]
[1.68478815e-04 3.30167226e-01 6.69664295e-01]
[3.54046163e-03 4.02267805e-01 5.94191734e-01]
[9.70617284e-01 2.93824740e-02 2.42443967e-07]
[2.56895205e-04 1.54631583e-01 8.45111522e-01]
[3.48668490e-02 9.11966141e-01 5.31670105e-02]
[1.47218847e-02 6.84038115e-01 3.01240001e-01]
[9.46510447e-04 4.28641987e-01 5.70411503e-01]
[9.64848137e-01 3.51516748e-02 1.87917880e-07]
[9.70436779e-01 2.95624025e-02 8.18591606e-07]]
The accuracy of the Logistic Regression is: 0.9833333333333333
The accuracy of the Logistic Regression is: 0.8666666666666667
## 查看混淆矩阵
confusion_matrix_result = metrics.confusion_matrix(test_predict,y_test)
print('The confusion matrix result:\n',confusion_matrix_result)
# 利用热力图对于结果进行可视化
plt.figure(figsize=(8, 6))
sns.heatmap(confusion_matrix_result, annot=True, cmap='Blues')
plt.xlabel('Predicted labels')
plt.ylabel('True labels')
plt.show()

通过结果我们可以发现,其在三分类的结果的预测准确度上有所下降,其在测试集上的准确度为:
86.67
%
86.67\%
86.67%,这是由于’versicolor’(1)和 ‘virginica’(2)这两个类别的特征,我们从可视化的时候也可以发现,其特征的边界具有一定的模糊性(边界类别混杂,没有明显区分边界),所有在这两类的预测上出现了一定的错误。
