本文目的:
对于K折交叉,想必大家都知道是什么原理。但是在具体实践中让你写的时候,你可能就会突然疑惑:“咦?道理我都懂,可是这个玩意儿到底怎么用。”
本文就是为了探讨一下什么时候 怎么用 K折交叉验证。
K折交叉(k-fold cross validation)
提到K折交叉,我想大部分人都了解其原理了。但是在这里还是先讲一下什么是K折交叉,防止有初学者是进来看什么是K折交叉的。
简言之,就是将数据随机分为K份,依次使用其中的K-1份进行训练,使用剩下的1份作为测试集。比较常见的有五折交叉、十折交叉。
可是道理我们都懂,但是实际写代码的时候遇到了问题就蒙了,因为K折交叉有两种实现思路:
方案1 不预先分出测试集
就是我们看书看博客最常见的说法。
- 将数据随机均分k份。
- 使用其中1份做测试集,剩余k-1份做训练集。
- 通过 k 次训练后,我们得到了 k 个不同的模型。
下图是一个五折交叉的例子:

方案2 提前分出测试集
- 将数据集分为训练集和测试集
- 将训练集分为 k 份
- 每次使用 k 份中的 1 份作为验证集,其他k-1份作为训练集
- 通过 k 次训练后,我们得到了 k 个不同的模型
- 从中挑选效果最好的超参数
- 使用最好的超参数模型,然后将 k 份数据全部作为训练集重新训练模型,得到最终模型
- 使用测试集测试最终的效果
以下也是五折交叉的例子:

分析
看到这里是不是突然开始迷惑了?那我到底该用哪一种?
我们来分析一下:
-
方案二,预先划分出测试集,训练之后也得到五个模型,但是取出其中较好的一个,测试集之外的所有数据合起来对其二次训练,训练之后作为最终的模型,并使用测试集评价其效果。
-
方案一,不提前留出测试集,直接所有数据放入模型中一边训练一边测试。这样我们最终会获得5个不同的模型,其之间的效果也会存在差异。
所以这五个模型,你最后要选哪个作为最终方案?
答案是选不出来,因为你没有单独的测试集,五个模型的数据不用,你无法最终验证究竟哪个模型的实际效果更好。
那你可以说:那我也和方案2一样,选出5个中看起来最好的那个模型的参数,然后把所有的数据塞回去重新训练……

你清醒一点,你一开始就没划分测试集,所以你不能把所有的数据再组合起来塞回去训练。因为训练完了你也没测试集看你训练的结果。那你又说:得到五个模型之后,我再把数据集划分出来,只取所有数据中的一部分作为训练集,剩下一部分测评模型。

清醒一点啊!!你怎么敢的!这属于学术作弊!!!你那五个模型怎么来的?所有数据训练出来的K-1份训练出来的!你这属于用训练集测试集混着用了!
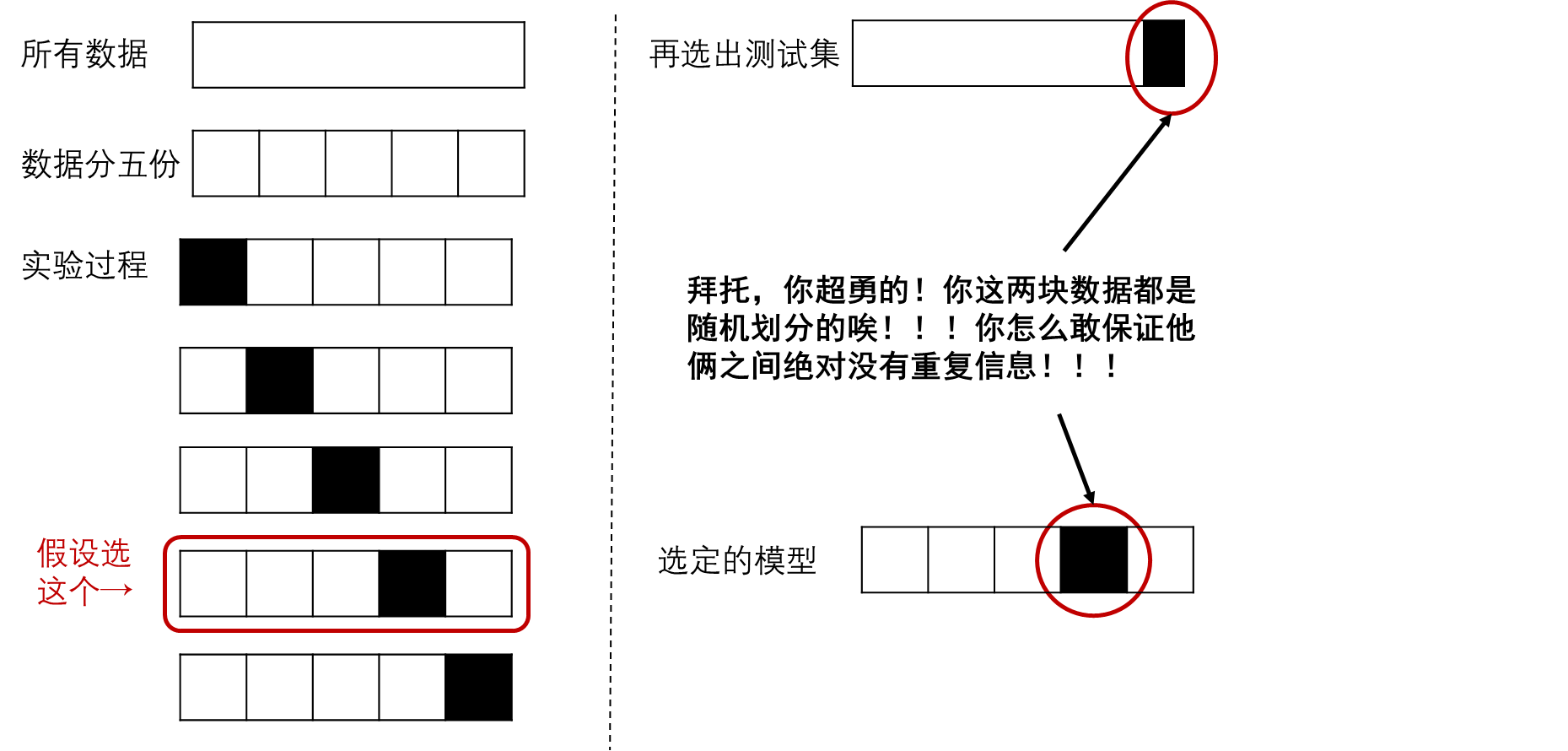
第二波分析:
先说个题外话,我们需要注意数据划分的作用:
-
训练集:训练模型,获得模型参数
模型参数怎么来的?不就是通过反向传播自动调整参数?
-
测试集:测试模型效果
最后测试你训练的模型效果如何。
-
验证集:调整模型超参数
训练过程中,想知道模型设计的好不好,那我们直接使用测试集测试吗?如果你有全部的数据,你确实可以这么做。但是有时候你可能得不到测试集数据,所以你怎么调参?你就需要自己划分出来一个验证集,检验模型性能。
换句话说就是在训练过程中手动调参,调整模型的超参数。
现在有两个模型放在你面前:
- 使用训练集训练,使用测试集测试,效果不好再回去调一调模型超参数。
- 使用训练集训练,使用验证集测试,效果不好回去调一调,调好之后使用测试集测试。
如果上述两个模型最终的测试效果是一样的,现在让你选一个模型,你觉得哪个好?我觉得,直觉上第二个模型的泛化性可能会更好。
因为第二个模型是在完全陌生的数据上进行测试,达到了某个效果。
而第一个模型是在对应的测试集上进行调参得到的最终效果,他的“好”可能仅限于那块测试集的数据,在其他数据上效果不一定比得过第二个模型。
现在回到我们的K折交叉。
方案1中只划分了训练集和测试集,如果你要调参,直接使用测试集调。
方案2中划分了训练集、验证集、测试集,你调参用验证集调,测试集仅作为最终模型测试。
那现在我们就明白了:
-
方案1中:使用测试集调整超参数的话,我们是尽力找到一个超参数能让所有的K-1个模型表现都更好一点,是为了找到比较好的一组超参数。
-
方案2中:使用验证集调整超参数,选出五个模型中看起来最好的,再使用训练集之外的所有数据再训练,最终使用测试集测试效果,这是为了选出一个最终可用的模型。
那我们就可以得出结论了。
所以什么时候用哪种?
方案1 不预先分出测试集:适用于评价模型效果,但是你没办法选出一个具体参数的模型。
就是当你说:我这个模型好!
好在哪里?
我进行K折交叉!出来的五个模型在我设计的超参数之下准确率都不错,所以我这个模型设计的挺好。
那让我用用你这个模型,什么参数下效果最好?
那我就不知道了,选不出来。
方案2 提前留出测试:适用于选择合适的模型。
我需要最终得到一个模型,你必须得要一个具体的模型,不仅有超参数,还要有一组能让模型表现“最好”的参数。这时候你就需要用方案2。
作者碎碎念,本文的写作初衷
月初时候写大作业,要求使用2折交叉验证,

起初我用的方案1,就是提前分出来测试集。然后我闲着没事和师姐交流了一下,师姐说:
???我突然就开始怀疑人生,是我做错了吗?
然后我开始查资料,越查越迷惑。直到最后师哥给我解答了疑惑:
感谢师哥答疑解惑,让我悟了。
我是萝莉安,我好像是个傻子。
