GNSS说第(七)讲—自适应动态导航定位(三)—Kalman滤波
Kalman滤波
Kalman滤波的显著特点是对状态空间进行估计,而状态空间估计一般是动态估计。Kalman滤波采用递推算法,即由参数的验前估值和新的观测数据进行状态参数的更新。如此Kalman滤波一般只需存储前一个历元的状态参数估值,无须存储所有历史观测信息。显然Kalman滤波具有很高的计算效率,并可进行实时估计。
Kalman滤波考虑了信号与测量值的基本统计特性(一阶、二阶统计特性),而且由于采用了状态空间概念,用状态方程描述系统,信号作为状态,所以它既能估计平稳的一维信号随机过程,又能估计非平稳的多维(向量)信号随机过程。
“滤波”是信号处理的重要工具,一般用于从具有噪声的数据中提取信号。基于这一定义,滤波在许多工程领域(如通信、雷达、导航、地震、大地测量、生物工程等)具有广泛应用。与滤波并行的有三个概念:滤波﹑平滑和预报。每一种运算都代表一种估计(Haykin,2002)。
“滤波”是指从所有观测信号(包括观测时刻t的观测数据)中提取信号的方法(邓自立,2000,2001)。
“平滑”是指从直到观测时刻t的观测信息中,提取实验过程中t’(t’<t)时的信号,即在求取t’时刻的信号时用到了t’以后的观测信号。
“预报”旨在导出观测之后的有用信号。
滤波可以分为线性滤波和非线性滤波。如果滤波的输出量是观测输入的线性函数,则称该滤波为线性滤波﹐否则称为非线性滤波。
线性最优滤波
假设已得到信号的某些统计参数(如均值和相关函数),同时也得到一些不想要的附加误差,线性滤波将这些具有误差的数据作为输人,按某种统计准则设计滤波系统,使误差对滤波输出的影响最小。实际上这是滤波最优化问题。通常采用的最优化准则为误差信号均方误差最小,而误差信号定义为理想信号与实际滤波输出信号之差。当输入信号为平稳序列时,由该准则可得到维纳(Wiener)滤波。
当信号或噪声处于非平稳状态时,维纳滤波不足以获得最优解,此时最优滤波必须适应于时变信号和噪声的处理。业已证明Kalman滤波在时变状态下能够获得最优解。
维纳滤波和卡尔曼滤波在连续时间序列和离散时间序列的信号处理中得到了较全面的发展。但在实践中,一般使用离散时间表示的维纳滤波和Kalman 滤波。对于连续的时间序列一般进行等间隔或非等间隔的离散化。如此,可使滤波信号输入,输出及滤波性质的讨论都变得相当简单。
自适应滤波
维纳滤波要求待处理的数据及其统计量的先验信息已知,输入、输出统计量与所设计滤波器依据的先验信息相吻合﹐如此可获得最优滤波解。然而,当这些信息不能满足要求时,所设计的滤波不可能获得最优解。自适应滤波正是为克服这一问题而发展起来的。所谓自适应滤波意味着具有自设计功能﹐即在递推计算过程中,当无从得知相关信号的特性时,也能获得比较满意的结果。自适应滤波算法从某些预知的初始条件开始,将人们所了解的信息尽可能地考虑进滤波系统。于是,在稳态情况下,经过迭代计算,自适应滤波应在某些统计准则下收敛于维纳滤波,而在非稳态情况下,该算法具有跟踪功能(Tracking Capability),即按某种统计量要求跟踪输人量随时间的变化。显然,自适应滤波的参数在迭代过程中不断更新,于是参数高度依赖观测信息。对于线性自适应滤波已有大量研究成果﹐然而实践中应该选择何种自适应滤波,仍然无统一定论,但一般应遵循如下原则:


线性自适应滤波的几种算法
线性自适应滤波解一般是不唯一的。有多种形式表示的自适应滤波算法,每一种算法都具有各自的理想特性。对于不同用户来说,必须首先了解各种自适应滤波的功能及局限性,然后选择适合自己特殊用途的自适应滤波算法。
在导航计算中,递推线性自适应滤波一般采用最小二乘(LS)算法。
最小二乘自适应滤波算法的损失函数或称运行指标定义为加权误差或残差平方和。这种误差定义为理想响应与实际滤波输出之差。最小二乘算法可以构造成递推估计或成批估计。成批处理技术将输入数据流分成等长的数据块(时间段),滤波的输入数据按一批一批处理。
递推最小二乘估计可以看成是特殊的Kalman滤波,一个区别是: Kalman滤波以状态空间表示,它提供了直到当前滤波时刻的所有用于滤波的输人的测度。
动力学模型

观测模型


Kalman滤波一般解算原理




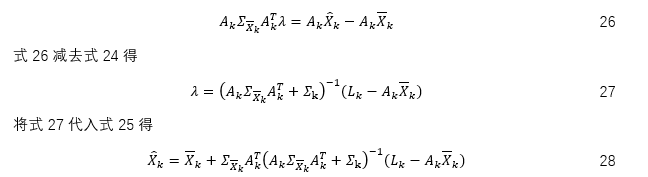


Kalman滤波新息向量及其性质
许多Kalman滤波解算模型的构造或推导都基于新息向量,或称预测残差向量。Kalman滤波的误差检验,计算方法的改进,自适应滤波的构造也大多基于新息向量。




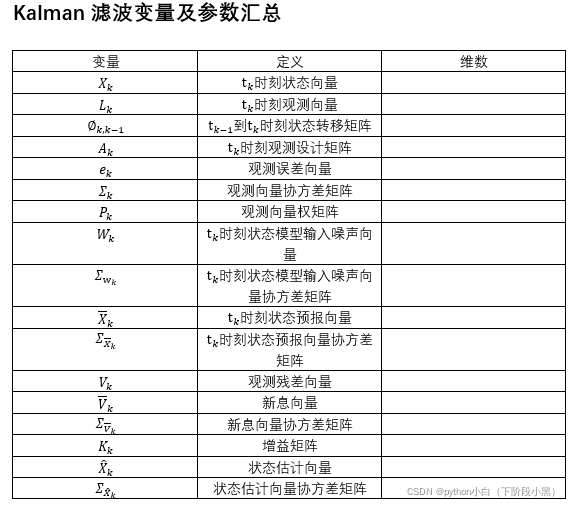
Kalman滤波简单小结

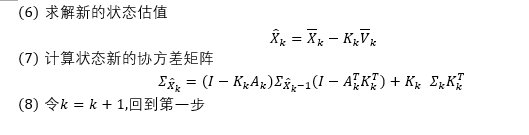
公式均为博主手动敲出,难免有误,恳请大家交流指正!
