1. 基本原理
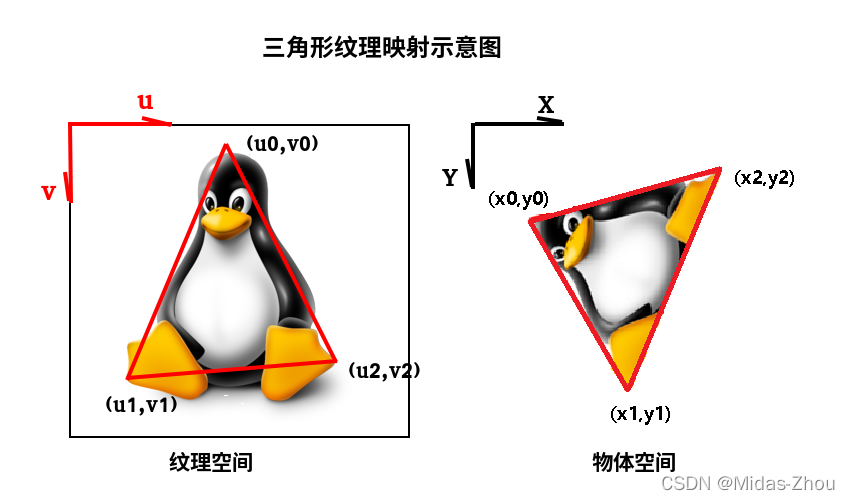
?如上图,已知物体空间中三角形的顶点坐标(x0,y0),(x1,y1),(x2,y2)分别对应到纹理空间坐标(u0,v0),(u1,v1),(u2,v2).?将他们的坐标值组合成3阶矩阵 matXYZ={ x0,y0,z0; x1,y1,z1; x2,y2,z2 } 和 matUV={ u0,v0,1.0; u1,v1,1.0; u2,v2,1.0 }
假设存在一个变换矩阵T, 使得下面等式成立:
???? matUV = matXYZ * matT? ?
如果matT有解, 那么可以得到:
???? matT = matIXYZ * matUV? (这里matIXYZ是matXYZ的逆阵)
矩阵matT就是从物体空间到纹理空间的映射变换矩阵.
一旦求出了matT, 那么物体空间三角形内的每一个像素点都可以映射到纹理空间中,并得到对应位置处的颜色值.
我们可以历遍物体空间三角形内的每一个像素点, 通过映射变换逐点上色, 最终得到完整的图像.
2. C语言程序实现
/*--------------------------------------------------------------------------------------------
@imgbuf: 纹理图像映像
@fb_dev: A pointer to FBDEV
@u/v: 纹理空间三角形坐标值 [0 1)
@x/y/z: 物理空间三角形顶点坐标数值
----------------------------------------------------------------------------------------------*/
void egi_imgbuf_mapTriWriteFB(EGI_IMGBUF *imgbuf, FBDEV *fb_dev,
float u0, float v0,
float u1, float v1,
float u2, float v2,
float x0, float y0, float z0,
float x1, float y1, float z1,
float x2, float y2, float z2 )
{
int i, k, kstart, kend;
int nl=0,nr=0; /* left and right point index */
int nm; /* mid point index */
float klr,klm,kmr;
float yu=0;
float yd=0;
float ymu=0;
float zu, zd;
long int locimg;
EGI_16BIT_COLOR color;
/* 0. Check input data */
if( imgbuf==NULL || imgbuf->imgbuf==NULL ) {
egi_dpstd("Input EGI_IMBUG is NULL or uninitiliazed!\n");
return;
}
int imgw=imgbuf->width;
int imgh=imgbuf->height;
/* 1. Mapping matrix computation 相关矩阵计算 */
/* 1.1 初始化矩阵 matUV,matT,matXYZ */
//float uvmat[3*3]={ u0, v0, 1.0f, u1, v1, 1.0f, u2, v2, 1.0f };
float uvmat[3*3]={ u0, v0, 0.0f, u1, v1, 0.0f, u2, v2, 0.0f };
float xyzmat[3*3]={x0, y0, z0, x1, y1, z1, x2, y2, z2};
float tmat[3*3]; /* Transform/map matrix */
float Ixyzmat[3*3]; /* Inversed xyzmat */
struct float_Matrix matUV;
matUV.nr=3; matUV.nc=3; matUV.pmat=uvmat;
struct float_Matrix matXYZ;
matXYZ.nr=3; matXYZ.nc=3; matXYZ.pmat=xyzmat;
struct float_Matrix matT;
matT.nr=3; matT.nc=3; matT.pmat=tmat;
struct float_Matrix matIXYZ;
matIXYZ.nr=3; matIXYZ.nc=3; matIXYZ.pmat=Ixyzmat;
/* 1.2 Inverse matXYZ 求矩阵matXYZ的逆阵matIXYZ */
if( Matrix_Inverse(&matXYZ, &matIXYZ)==NULL ) {
egi_dpstd("Fail to inverse matrix_XYZ!\n");
return;
}
/* 1.3 matT = matIXYZ*matUV 求映射矩阵matT */
Matrix_Multiply(&matIXYZ, &matUV, &matT);
/* 2. Define matPuv and matPxyz */
float ptuv[3]={0,0,1.0f}; /* U,V,1 */
struct float_Matrix matPuv;
matPuv.nr=1; matPuv.nc=3; matPuv.pmat=ptuv;
float ptxyz[3]={0,0,0};
struct float_Matrix matPxyz;
matPxyz.nr=1; matPxyz.nc=3; matPxyz.pmat=ptxyz;
/* 3. Define point array */
struct float_3dpoints {
float x; float y; float z;
} points[3];
points[0].x=x0; points[0].y=y0; points[0].z=z0;
points[1].x=x1; points[1].y=y1; points[1].z=z1;
points[2].x=x2; points[2].y=y2; points[2].z=z2;
/* 4. Find Left, Right and Mid. point 排列三角形左中右顶点次序 */
/* Cal nl, nr */
for(i=1;i<3;i++) {
if(points[i].x < points[nl].x) nl=i;
if(points[i].x > points[nr].x) nr=i;
}
/* TODO: If three points are collinear OR degenerated into one point. */
/* get x_mid point index */
nm=3-nl-nr;
/* 5. Compute side slopes. 计算边线的斜率 */
/* Ruled out (points[nr].x == points[nl].x), as nl==nr. */
klr=1.0*(points[nr].y-points[nl].y)/(points[nr].x-points[nl].x);
if(points[nm].x != points[nl].x) {
klm=1.0*(points[nm].y-points[nl].y)/(points[nm].x-points[nl].x);
}
else
klm=1000000.0;
if(points[nr].x != points[nm].x) {
kmr=1.0*(points[nr].y-points[nm].y)/(points[nr].x-points[nm].x);
}
else
kmr=1000000.0;
//printf("klr=%f, klm=%f, kmr=%f \n",klr,klm,kmr);
/* 6. 三角形左侧部分的映射 Left part of the triangle: traverse pixels and map to get color value. */
for( i=0; i<roundf(points[nm].x-points[nl].x+1); i++)
{
/* 从左向右竖线扫描 */
yu=klr*i+points[nl].y;
yd=klm*i+points[nl].y;
zu=points[nl].z+(points[nr].z-points[nl].z)*i/(points[nr].x-points[nl].x);
zd=points[nl].z+(points[nm].z-points[nl].z)*i/(points[nm].x-points[nl].x);
if(yu>yd) {
kstart=roundf(yd);
kend=roundf(yu);
}
else {
kstart=roundf(yu);
kend=roundf(yd);
}
/* 竖线各点的映射 Traverse pixels on the vertical line */
for(k=kstart; k<=kend; k++) {
ptxyz[0]=i+points[nl].x; //X
ptxyz[1]=k; //Y
ptxyz[2]=zd+(zu-zd)*(k-yd)/(yu-yd); //Z
/* matPuv =matPxyz*matT */
if( Matrix_Multiply(&matPxyz, &matT, &matPuv)==NULL ) {
egi_dpstd("Fail to do matPuv =matPxyz*matT!\n");
//return;
}
/* 这里直接得到最近点的颜色值, 也可参考7.的方法. */
/* image data location */
locimg=(roundf(ptuv[1]*imgh))*imgw+roundf(ptuv[0]*imgw); /* roundf */
if( locimg>=0 && locimg < imgh*imgw ) {
fbset_color2(fb_dev,imgbuf->imgbuf[locimg]);
draw_dot(fb_dev, roundf(points[nl].x+i), k); // k as y
}
}
}
/* 7. 三角形右侧部分的映射 Right part of the triangle: traverse pixels and map to get color value. */
ymu=yu;
for( i=0; i<roundf(points[nr].x-points[nm].x+1); i++)
{
/* 从左向右竖线扫描 */
yu=klr*i+ymu;
yd=kmr*i+points[nm].y;
zu=points[nl].z+(points[nr].z-points[nl].z)*(points[nm].x-points[nl].x+i)/(points[nr].x-points[nl].x);
zd=points[nm].z+(points[nr].z-points[nm].z)*i/(points[nr].x-points[nm].x);
if(yu>yd) { kstart=roundf(yd); kend=roundf(yu); }
else { kstart=roundf(yu); kend=roundf(yd); }
/* 竖线各点的映射 Traverse pixels on the vertical line */
for(k=kstart; k<=kend; k++) {
ptxyz[0]=i+points[nm].x;
ptxyz[1]=k;
ptxyz[2]=zd+(zu-zd)*(k-yd)/(yu-yd);
/* matPuv =matPxyz*matT */
if( Matrix_Multiply(&matPxyz, &matT, &matPuv)==NULL ) {
egi_dpstd("Fail to do matPuv =matPxyz*matT!\n");
//return;
}
/* 这里用双线性插值计算得到颜色值 */
if( egi_imgbuf_uvToPixel(imgbuf, ptuv[0], ptuv[1], &color, NULL)==0 ) {
fbset_color2(fb_dev, color);
draw_dot(fb_dev, roundf(points[nm].x+i), k); // k as y
}
}
}
}
参考:?? <计算机图形学基础教程 第2版> (孔令德 编著) P314
更多代码见 https://github.com/widora/wegi.git
3. 有待改进处:
3.1 纹理坐标是2维的,而物体坐标是3维的,这种情况下如何处理使得matT恒定可解.
3.2 未考虑三角形退化成一点或一线的情况.
4. 其他方法
还可以应用三角形重心坐标系法来进行纹理映射计算, 更多代码见 https://github.com/widora/wegi.git
5. 效果如下 (固定图像为纹理图像)
?? 变换图像的左侧部分应用了近似插值, 右侧部分应用了双线性插值, 对比效果明显. 特别是图3和图4.

?
?
?
?
