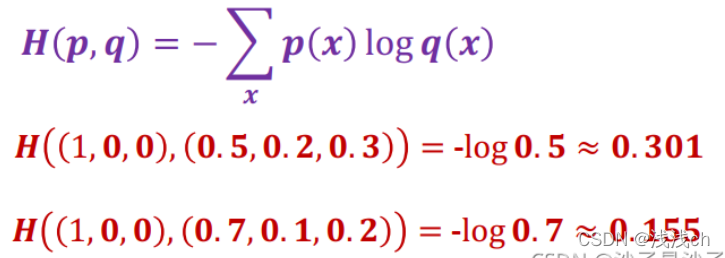（一）什么是Sigmoid函数和softmax函数？
提到二分类问题容易想到逻辑回归算法，而逻辑回归算法最关键的步骤就是将线性模型输出的实数域映射到[0, 1]表示概率分布的有效实数空间，其中Sigmoid函数和softmax函数刚好具有这样的功能。
1.1 Sigmoid函数
Sigmoid =多标签分类问题=多个正确答案=非独占输出（例如胸部X光检查、住院）。构建分类器，解决有多个正确答案的问题时，用Sigmoid函数分别处理各个原始输出值。
Sigmoid函数的输出在(0,1)之间，输出范围有限，优化稳定，可以用作输出层。
1.2 Softmax函数
Softmax =多类别分类问题=只有一个正确答案=互斥输出（例如手写数字，鸢尾花）。构建分类器，解决只有唯一正确答案的问题时，用Softmax函数处理各个原始输出值。Softmax函数的分母综合了原始输出值的所有因素，这意味着，Softmax函数得到的不同概率之间相互关联。
Softmax直白来说就是将原来输出是3,1,-3通过Softmax函数一作用，就映射成为(0,1)的值，而这些值的累和为1（满足概率的性质），那么我们就可以将它理解成概率，在最后选取输出结点的时候，我们就可以选取概率最大（也就是值对应最大的）结点，作为我们的预测目标。
由于Softmax函数先拉大了输入向量元素之间的差异（通过指数函数），然后才归一化为一个概率分布，在应用到分类问题时，它使得各个类别的概率差异比较显著，最大值产生的概率更接近1，这样输出分布的形式更接近真实分布。
1.3 对于二分类任务
对于二分类问题来说，理论上，两者是没有任何区别的。由于我们现在用的Pytorch、TensorFlow等框架计算矩阵方式的问题，导致两者在反向传播的过程中还是有区别的。实验结果表明，两者还是存在差异的，对于不同的分类模型，可能Sigmoid函数效果好，也可能是Softmax函数效果。
1.4 总结
1、如果模型输出为非互斥类别，且可以同时选择多个类别，则采用Sigmoid函数计算该网络的原始输出值。
2、如果模型输出为互斥类别，且只能选择一个类别，则采用Softmax函数计算该网络的原始输出值。
3、Sigmoid函数可以用来解决多标签问题，Softmax函数用来解决单标签问题。
4、对于某个分类场景，当Softmax函数能用时，Sigmoid函数一定可以用。
5、对于二分类问题，二者不等同，要结合实际选择处理函数。
补充：
Softmax+交叉熵损失函数在Pytorch中的处理：直接接上torch.nn.CrossEntropyLoss()方法；
Sigmoid+损失函数在Pytorch中的处理：直接接上torch.nn.BCEWithLogitsLoss()方法。
Softmax+交叉熵损失函数在Tensorflow中的处理：tf.keras.losses.categorical_crossentropy()方法；
而Tensorflow中求hardmax也就是直接求最大值时的处理：tf.reduce_max([1, 2, 3, 4, 5])方法，在numpy中求最大值直接用：np.max()方法。
（二）CrossEntropy交叉熵损失函数
1、交叉熵损失函数经常用于分类问题中，特别是在神经网络做分类问题时，也经常使用交叉熵作为损失函数，此外，由于交叉熵涉及到计算每个类别的概率，所以交叉熵几乎每次都和sigmoid(或softmax)函数一起出现。
我们用神经网络最后一层输出的情况，来看一眼整个模型预测、获得损失和学习的流程：
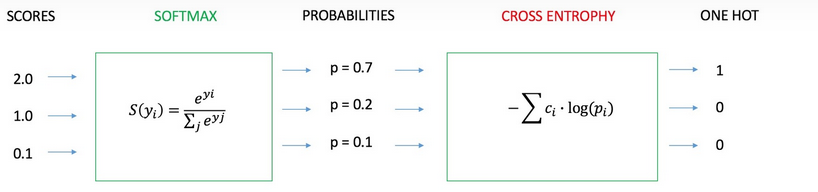
1、神经网络最后一层得到每个类别的得分scores（也叫logits）；
2、该得分经过sigmoid(或softmax)函数获得概率输出；
3、模型预测的类别概率输出与真实类别的one hot形式进行交叉熵损失函数的计算。
2、Cross Entropy Loss Function（交叉熵损失函数）表达式
（1）二分类
（2）多分类
3、图像分类任务实例
（1）我们希望根据图片动物的轮廓、颜色等特征，来预测动物的类别，有三种可预测类别：猫、狗、猪。假设我们当前有两个模型（参数不同），这两个模型都是通过sigmoid/softmax的方式得到对于每个预测结果的概率值：
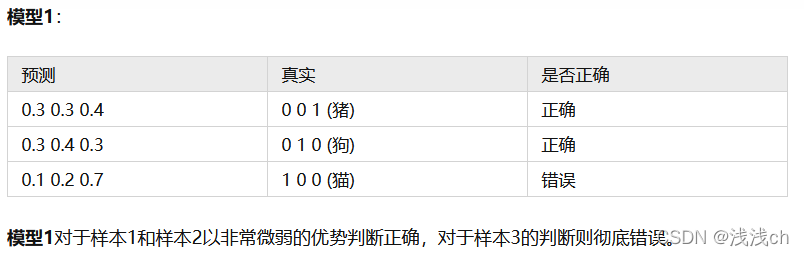
（2）接下来通过交叉熵损失函数来判断模型在样本上的表现：
根据多分类问题的计算公式可算。
可以看出模型2的预测效果更好。
上述过程可以使用python的sklearn库：
from sklearn.metrics import log_loss
y_true = [[0, 0, 1], [0, 1, 0], [1, 0, 0]]
y_pred_1 = [[0.3, 0.3, 0.4], [0.3, 0.4, 0.3], [0.1, 0.2, 0.7]]
y_pred_2 = [[0.1, 0.2, 0.7], [0.1, 0.7, 0.2], [0.3, 0.4, 0.3]]
print(log_loss(y_true, y_pred_1))
print(log_loss(y_true, y_pred_2))
____________
1.3783888522474517
0.6391075640678003
（三）加深理解–交叉熵损失函数
1、信息熵
2、相对熵（KL散度）
3、交叉熵
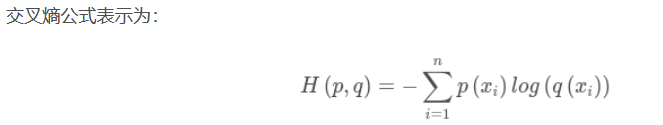
在机器学习中，信息熵在这里就是一个常量。由于KL散度表示真实概率分布与预测概率分布的差异，越小表示预测的结果越好，所以最小化KL散度的值；交叉熵等于KL散度加信息熵（常量），相比KL散度更加容易计算，所以一般在机器学习中直接用交叉熵做loss。
交叉熵表示为真实概率分布与预测概率分布之间的差异，并且交叉熵的值越小，说明模型结果越好。其通常与softmax搭配进行分类任务的损失计算。
在分类任务中，交叉熵损失函数定义成这样：
4、交叉熵损失函数计算案例
假设有一个3分类问题，某个样例的正确答案是（1， 0， 0）
甲模型经过softmax回归之后的预测答案是（0.5， 0.2， 0.3）
乙模型经过softmax回归之后的预测答案是（0.7， 0.1， 0.2）
