核心概念?
| 概念 | 说明 | |
| 编程范式 | 数据流图 | 编程范式:声明式?vs命令式 有向无环图 |
| 数据流图节点,叫操作(OP) | 数学函数或表达式 | MatMul BiasAdd Softmax |
| 变量 | Variable | |
| 占位符 | placeholder | |
| 梯度值 | Gradients | |
| 更新参数操作 | ||
| 流图执行方式 | 拓扑排序后执行 | |
| 数据载体 | 张量Tensor | n维数组 每个量的数组元素类型是确定的。 存储在一段连接的空间 如int[N][M][L] dtype: int shape: [N,M,L] tensorfow支持丰富的类型:tf.int64 |
| 常量张量 | a=tf.constant(1.0) | |
| 变量张量 | b=tf.variable(2.0) | |
| 稀疏张量 | tf.SparseTensor | |
| 张量操作 | 数学操作 | +-*/ tf.add tf.sub tf.abs tf.neg tf.invert |
| 形状操作 | chip, reshape, slice, shuffle | |
| 归约操作 | reduce_mean reduce_sum | |
| 神经网络操作? ?? | conv, pool, softmax, relu | |
| 条件操作 | cond | |
| 计算结点:OP | name, type, inputs, control_inputs, outputs, device,graph,traceback | |
| 存储结点:Variable | name, dtype, shape, initial_value, initializer, device,graph, op | |
| 数据结构:placeholder | name, dtype, shape | |
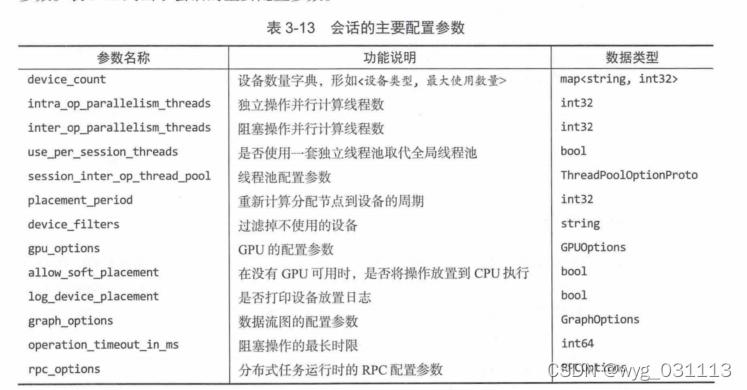
| 运行环境 | 会话:Session(target, graph, cnofig) | sess.run(fetches, feed_dict, options, run_metadata) sess.close |
|
交互式会话:Inter
activeSession
| ||
| 训练工具:优化器 |
损失函数与优化算法
|
minimize
方法
.
计算梯度
|


?
?
?最佳实践
tensorflow训练模模型8个步骤
- 定义超参数;
- 输入数据
- 构建模型;
- 定义损失函数;
- 创建优化器;
- 定义单步 练操作
- 创建会话;
- 迭代训练
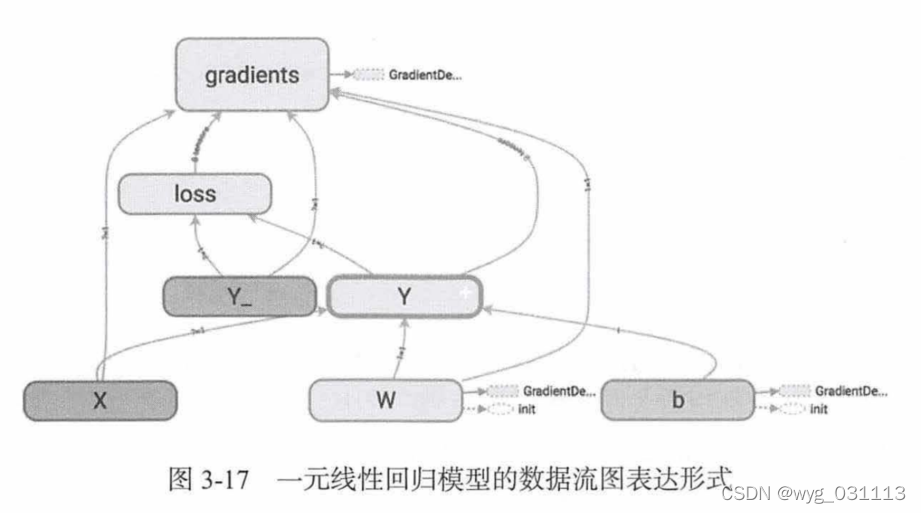
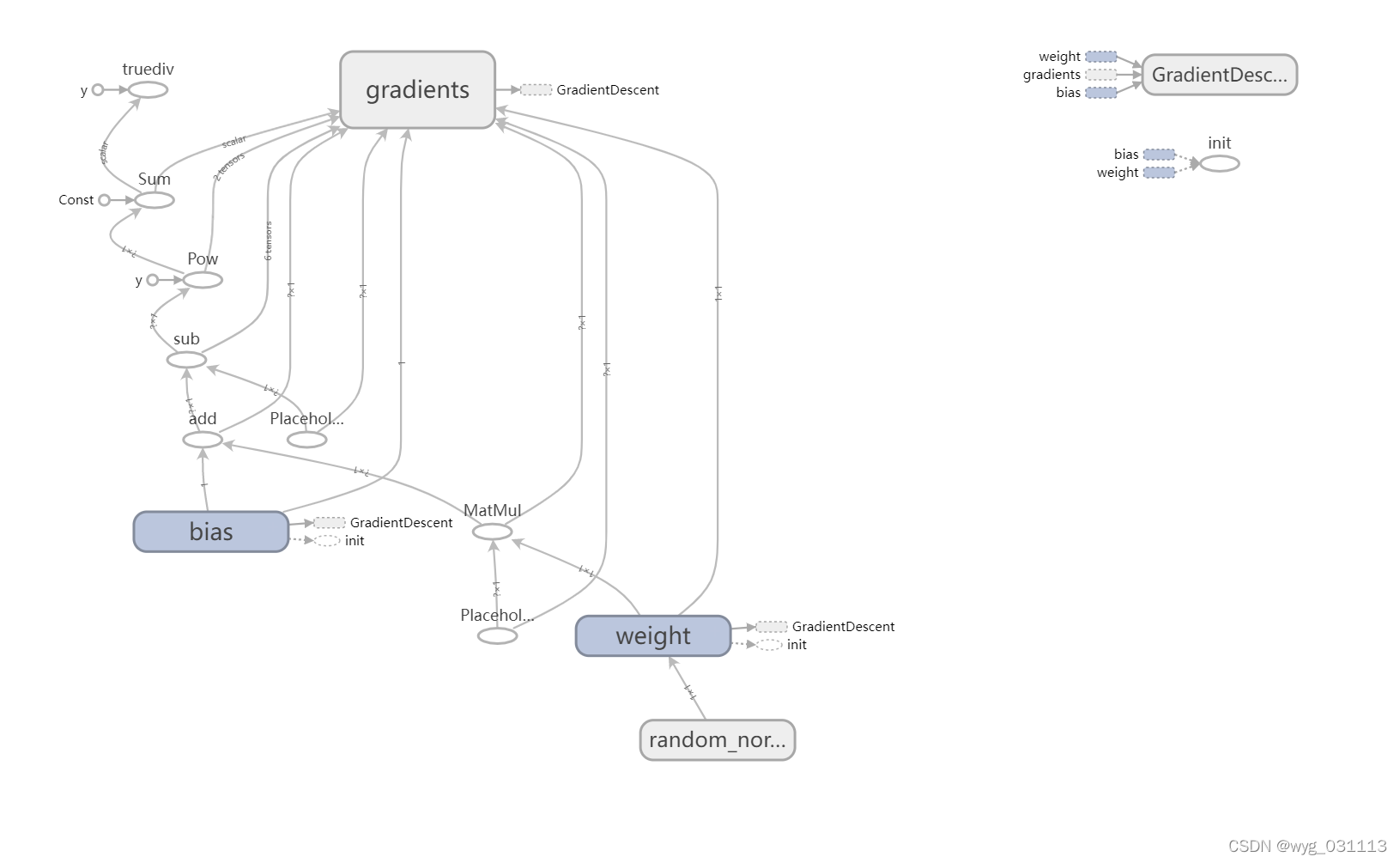
一元线性回归模型
Y=w*X+b
import tensorflow.compat.v1 as tf
import numpy as np
tf.disable_v2_behavior()
tf.disable_eager_execution ()
#超参数
#学习率
learning_rate = 0.01
#训练迭代最大步数
max_train_step = 1000
#输入数据
#监督学习中,数据集分为训练集( training set )、验 证集( validation set ) 和测试集(test set)
train_X = np.array([[3.3], [4.4], [5.5], [6.71], [6.93], [4.168], [9.779], [6.182], [7.59], [2.167],[7.042], [10.791], [5.313], [7.997], [5.654], [9.27], [3.1]], dtype=np.float32)
train_Y = np.array([[1.7], [2.76], [2.09], [3.19], [1.694], [1.573], [3.366], [2.596], [2.53], [1.221], [2.827], [3.465], [1.65], [2.904], [2.42], [2.94], [1.3]], dtype=np.float32)
total_samples = train_X.shape[0]
print(train_X)
print(train_Y)
#构建模型
#输入数据X
X = tf.placeholder(tf.float32, [None, 1])
#模型参数W,b
W = tf.Variable(tf.random_normal([1,1]), name="weight")
b = tf.Variable(tf.zeros([1]), name="bias")
#推理值Y
Y = tf.matmul(X, W) + b
#定义损失函数
#实际输入值
Y_ = tf.placeholder(tf.float32, [None, 1])
#损失 均方差
loss = tf.reduce_sum(tf.pow(Y-Y_,2))/(total_samples)
#创建优化器
#梯度下降法
optimizer = tf.train.GradientDescentOptimizer(learning_rate)
#单步训练操作
train_op = optimizer.minimize(loss)
#创建会话
log_step = max_train_step/20
#导出模型到tensorboard
summary_writer = tf.summary.FileWriter('tb_log/', flush_secs=1)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
print("start trainning")
for step in range(max_train_step):
if step % log_step == 0:
c = sess.run(train_op, feed_dict={X:train_X, Y_: train_Y})
if step % log_step == 0:
c = sess.run(loss, feed_dict={X:train_X, Y_: train_Y})
print("Step:%d, loss==%.4f, W=%.4f, b==%.4f" % (step, c, sess.run(W), sess.run(b)))
print("train finish")
#训练完成,计算损失,应当在test数据集上计算,这里就在训练集上吧
final_loss = sess.run(loss, feed_dict={X:train_X, Y_: train_Y})
weight, bias = sess.run([W, b])
print("Step:%d, loss==%.4f, W=%.4f, b==%.4f" % (max_train_step, final_loss, weight, bias))
print("Linear Regression Model: Y=%.4f*X+%.4f" % (weight, bias))
summary_writer.add_graph(sess.graph)#添加graph图
summary_writer.close()
#模型可视化
%matplotlib inline
import matplotlib.pyplot as plt
plt.plot(train_X, train_Y, 'ro', label='Training Data')
plt.plot(train_X, weight * train_X + bias, label='Fitted line')
plt.legend()
plt.show()运行结果:
start trainning
Step:0, loss==0.3116, W=0.3104, b==0.0604
Step:50, loss==0.2207, W=0.3503, b==0.0679
Step:100, loss==0.2196, W=0.3540, b==0.0702
Step:150, loss==0.2192, W=0.3541, b==0.0720
Step:200, loss==0.2189, W=0.3539, b==0.0738
Step:250, loss==0.2186, W=0.3537, b==0.0755
Step:300, loss==0.2183, W=0.3534, b==0.0773
Step:350, loss==0.2180, W=0.3532, b==0.0791
Step:400, loss==0.2177, W=0.3529, b==0.0808
Step:450, loss==0.2174, W=0.3527, b==0.0825
Step:500, loss==0.2171, W=0.3524, b==0.0843
Step:550, loss==0.2168, W=0.3522, b==0.0860
Step:600, loss==0.2164, W=0.3519, b==0.0878
Step:650, loss==0.2161, W=0.3517, b==0.0895
Step:700, loss==0.2158, W=0.3514, b==0.0912
Step:750, loss==0.2155, W=0.3512, b==0.0929
Step:800, loss==0.2152, W=0.3510, b==0.0946
Step:850, loss==0.2149, W=0.3507, b==0.0963
Step:900, loss==0.2146, W=0.3505, b==0.0980
Step:950, loss==0.2144, W=0.3502, b==0.0997
train finish
Step:1000, loss==0.2144, W=0.3502, b==0.0997
Linear Regression Model: Y=0.3502*X+0.0997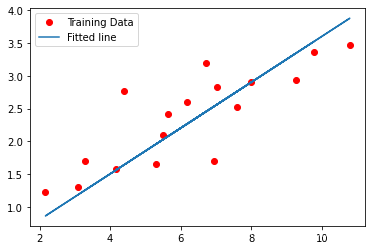
?
