[人工智能]第四章 向量组的线性相关性

向量组及其线性组合

• 定义1
  n 个有次序的数 a₁,a₂,…,a_n所组成的数组称为 n 维向量，这 n 个数称为该向量的 n 个分量，第 i 个数 a_i称为第 i 个分量

分量全为实数的向量称为实向量，分量全为复数的向量称为复向量

1. 列向量与行向量
   
   
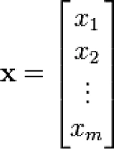
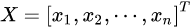
2. 向量组
   若干个同维数的列向量(或同维数的行向量)所组成的集合叫做向量组

• 定义2
  

• 定理1
  向量 b 能由向量组 A: a₁, a₂, …, a_m 线性表示的充分必要条件是矩阵 A = (a₁, a₂, …, a_m)的秩等于矩阵 B = (a₁, a₂, …, a_m, b)
  若向量组 A 与向量组 B 能相互线性表示，则称这两个向量组等价

这个定理加粗了，手写了，重要性极高！！！

• 应用
  • 求向量 b 能被 向量组 a 线性表示的表达式
  • 求向量组 a、b 等价

向量组的线性相关性

• 定理4
  向量组 A: a₁, a₂, …, a_m 线性相关的充分必要条件是它所构成的矩阵 A = (a₁, a₂, …, a_m) 的秩小于向量个数 m；向量组 A 线性无关的充分必要条件是 R(A) = m

• 应用
  • 求向量组是否线性相关（重要例题 P₈₉）

向量组的秩

若向量组 A 线性无关，则 A 自身就是它的最大无关组，而其秩就等于它所含向量的个数

定理6 矩阵的秩等于它的列向量组的秩，也等于它的行向量组的秩

• 应用
  • 求最大无关组（重要例题 P₉₄）
    
    
    
    

线性方程组的解的结构

• 性质1
  若 x = ξ₁，x = ξ₂ 为向量组 Ax = 0 的解，则 x = ξ₁ + ξ₂ 也是向量方程的解

• 性质2
  若 x = ξ₁ 为向量方程 Ax = 0 的解，k 为实数，则 x = kξ₁ 也是向量方程的解

齐次线性方程组的解集的最大无关组称为该齐次线性的基础解系

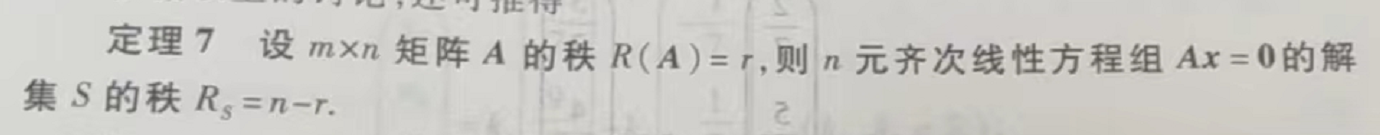
• 应用
  求齐次线性方程组的基础解系和通解（重要例题 P_99-100）

• 性质3
  设 x = η₁ 及 x = η₂ 都是向量方程 Ax = b 的解，则 x = η₁ - η₂ 为对应的齐次线性方程组 Ax = 0 的解

• 性质4
  设 x = η 是方程 Ax = b 的解，x = ξ 是方程 Ax = 0 的解，则 x = η + ξ 仍是方程 Ax = b 的解

非齐次方程的通解 = 对应的齐次方程的通解 + 非齐次方程的一个特解

• 应用
  求非齐次方程的通解（重要例题 P_103-104）

阅读世界，共赴山海

423全民读书节，邀你共读