但其原生Self-Attention 的计算复杂度问题一直没有得到解决,Self-Attention 需要对输入的所有N个 token 计算 [公式] 大小的相互关系矩阵,考虑到视觉信息本来就就是二维(图像)甚至三维(视频),分辨率稍微高一点这计算量就很难低得下来。
Swin Transformer 想要解决的计算复杂度的问题。
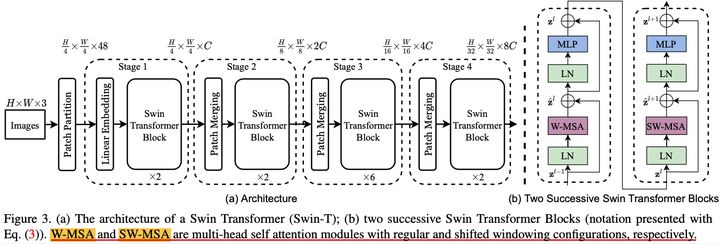
1. 网络结构
简单来说就是,原生 Transformer 对 N 个 token 做 Self-Attention ,复杂度为 O ( N 2 ) O(N^2) O(N2) ,
Swin Transformer 将 N 个 token 拆为 N/n 组,(n设为常数 ;
每组 n个token 进行计算,复杂度降为
O
(
N
?
n
2
)
O(N*n^2)
O(N?n2) ,考虑到 n 是常数,那么复杂度其实为
O
(
N
)
O(N)
O(N) 。
2. 两个问题
分组计算的方式虽然大大降低了 Self-Attention 的复杂度,但与此同时,有两个问题需要解决,
-
其一是分组后 Transformer 的视野局限于 n 个token,看不到全局信息;
-
其二是组与组之间的信息缺乏交互。
2.1 分层
对于问题一,Swin Transformer 的解决方案即 Hierarchical,每个 stage 后对 2x2 组的特征向量进行融合和压缩(空间尺寸 H ? W ? > H 2 ? W 2 H * W -> \frac{H}{2} * \frac{W}{2} H?W?>2H??2W?,特征维度 $ C-> 4C -> 2C$),这样视野就和 CNN-based 的结构一样,随着 stage 逐渐变大。
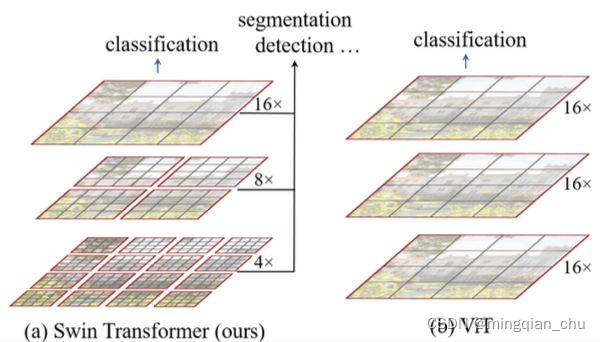
2.2 shifted windows;
对于问题二,Swin Transformer 的解决方法是 Shifted Windows,如下图所示:
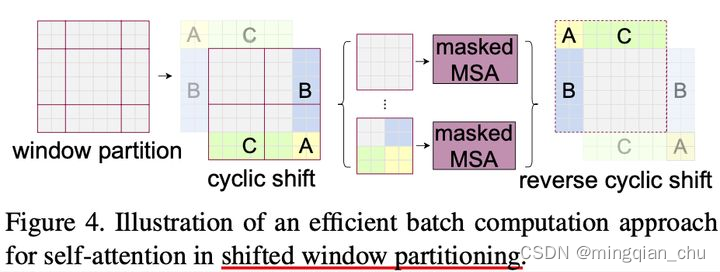
通过 Shifted Windows 的方式,使相邻的组(patch)进行信息交互,思想上其实和shufflenet 类似,不过这里是空间邻接上的shuffle,而shufflenet是通道维度的shuffle。
此外还有一个细节就是在计算 Self-Attention 时,使用了 Relative position bias,
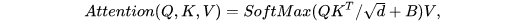
B 为可学习的参数,作用与 Local Relation Networks for Image Recognition中的Geometry Prior 类似。
