背景
现在我对比了14个模型在某个数据集上的预测性能,得到了14个 R 2 R^2 R2值,但因为它取值范围是 ( ? ∞ , 1 ] (-\infty,1] (?∞,1] ,所以有不少很负的值。
这是数据
data = [ 0.9733, 0. , 0.0566, -9.654 , 0.1291, -0.0926, -0.0661, -2.3085, 0. , -10.63 , 0., -3.797 ,-7.592 , 0. ]
做可视化的时候,其实是有点困难的。比如说用柱状图可视化成下面这种样子
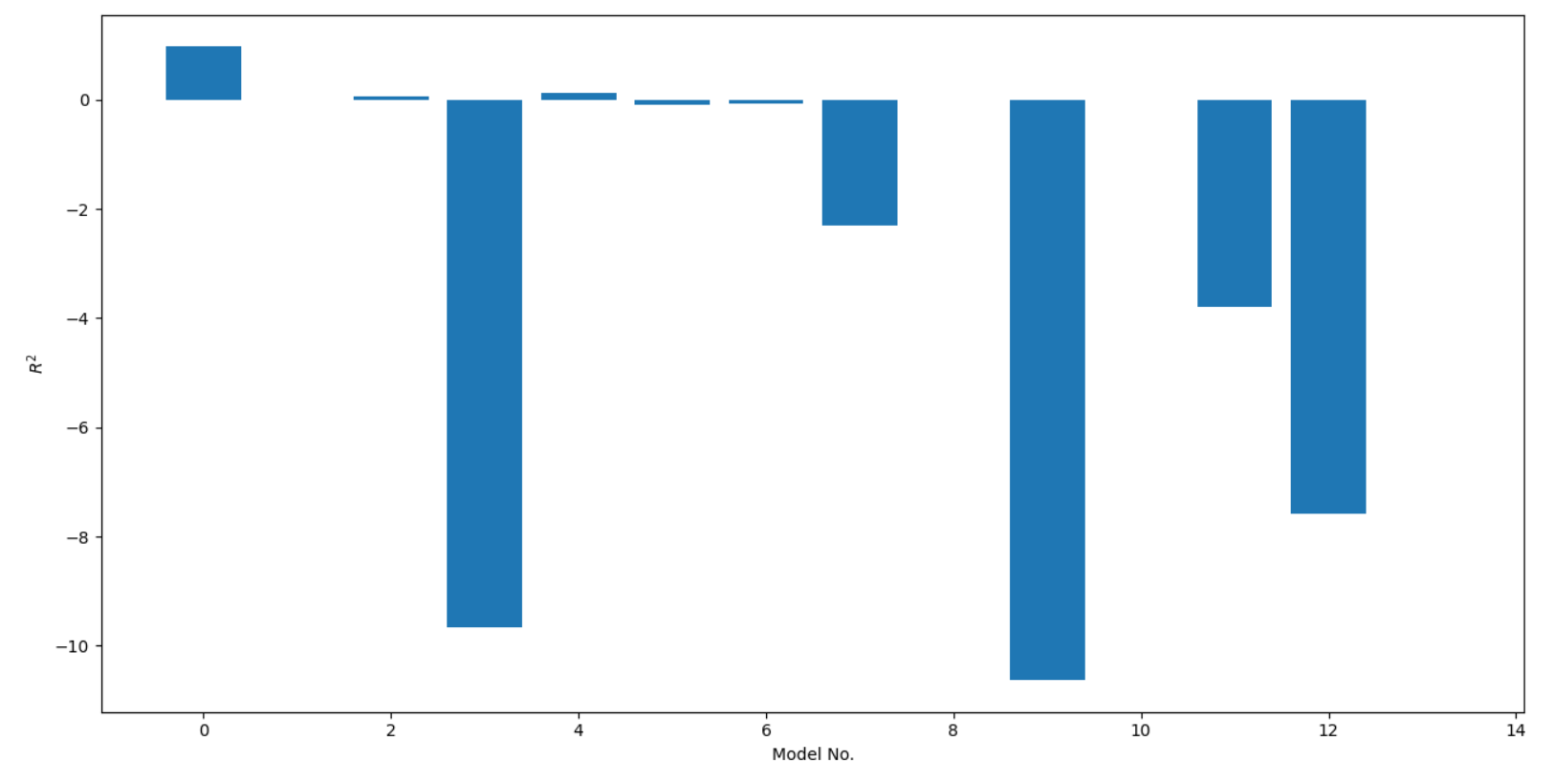
Emmm 很难看啊,其实你负的再多,对我来说也没啥意义,我关注的主要是正半轴的部分,现在因为负数的太负,几个正数的 R 2 R^2 R2 ,反倒没啥区别了。这个时候我希望的就是,能不能把负半轴压缩压缩,把正半轴拉伸拉伸?
方案一(题外话)
我首先想到的方案是断裂坐标轴,这个可以用brokenaxes这个package实现(pip install)。这个我不展开讲,不是重点。
from brokenaxes import brokenaxes
x = np.arange(14)
ylims = ((-10.8, -10.4), (-9.8, -9.6), (-7.8, -7.4), (-3.9, -3.6), (-2.4, -2.2), (-0.18, 1.14))
bax = brokenaxes(
ylims=ylims, # 连续的区间
hspace=0.05, # y轴裂口宽度
wspace=0.05, # x轴裂口宽度
despine=False, # 是否只显示单侧裂口(没有上坐标轴和右坐标轴)
d=0.007, # 裂口斜线长度
diag_color='red', # 裂口斜线颜色
tilt=45 # 裂口斜线倾角
)
# 使用bax绘图使用和matplotlib.axes._subplots.AxesSubplot绘图的方法基本一致
bax.bar(x, data[:, 2], facecolor='#ff9999', width=0.4)
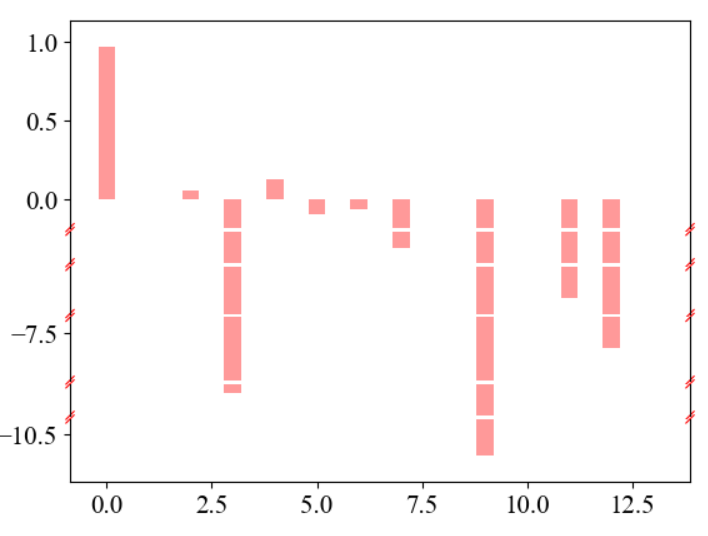
方案二 自定义scale
理论部分

以上是matplotlib自带的scale,最常用的、也是默认设置,就是Linear Scale。Log scale适合可视化数量级很大或者很小(接近0)的数据,它实际上做的事情是把真实世界的
x
x
x,映射到图上的
lg
?
x
\lg x
lgx 的位置,但是刻度标注的还是
x
x
x 。
但是对于很大(小)的负数,因为定义域的问题, lg ? x \lg x lgx 就无能为力了,Symmetric Log Scale做的是把正半轴的对数标度对称到负半轴上,让这些负数也能用对数标度可视化。
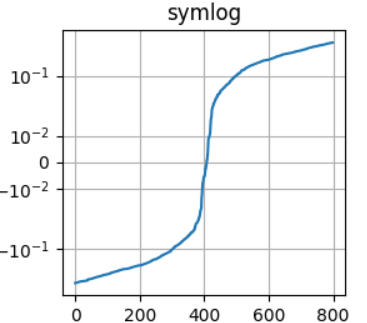
再来看看我们的需求,需要**压缩负数区间,拉伸 [ 0 , 1 ] [0,1] [0,1] 区间!**什么样的函数可以做到这一点呢?先大致画一下函数图像吧
我想大致应该这样,x轴在哪儿不重要,唯一的目标就是压缩负的,拉伸正的!像这样的函数,我们可能会想到 y = a x y=a^x y=ax ,或者是 y = 1 / ( b ? x ) y=1/(b-x) y=1/(b?x) 之类的。就这俩而言,哪个更好呢?我想可能是分式函数好一点,因为 b b b 这个参数,可以帮助我们规定:越靠近 b b b 的地方,得增长越快。结合我们的需求, R 2 ? 1 R^2\leqslant1 R2?1 恒成立,而 R 2 R^2 R2 越接近1,预测得越好, R 2 R^2 R2 从0.99提升到0.999的难度,比从0.9提升到0.99得难度大得多。所以我们可以把这个 b b b 设置成大于且接近1的一个值。实操中,我取了 1.6。
有了理论,现在看看怎么变现。FuncScale 这个类挺好,给了我们自定义scale的接口,这样我就不用自己重写一个Scale 类了。实际上呢,在代码中,我们也不用import这个FuncScale,因为它已经 register 了。我们要做的事情,就是像之前使用对数坐标那样(ax.set_yscale('log'))来设置自定义函数的标度,即ax.set_yscale('function', (forward, inverse))
这边多了forward和inverse,分别为映射函数和其反函数,结合我们的例子,就是
f
o
r
w
a
r
d
(
x
)
=
1
b
?
x
\mathrm{forward}(x)=\frac{1}{b-x}
forward(x)=b?x1?
i n v e r s e ( x ) = b ? 1 y \mathrm{inverse}(x)=b-\frac{1}{y} inverse(x)=b?y1?
核心代码
核心部分讲完了,下面给出完整代码!
from matplotlib import pyplot as plt, font_manager as fm
import numpy as np
from matplotlib.ticker import NullFormatter, FixedLocator
def forward(x):
x = 1 / (frac_b - x)
return x
def inverse(x):
x = frac_b - 1 / x
return x
data = [ 0.9733, 0. , 0.0566, -9.654 , 0.1291, -0.0926, -0.0661, -2.3085, 0. , -10.63 , 0., -3.797 ,-7.592 , 0. ]
x = np.arange(14)
plt.rc('font', family='Times New Roman', size=15)
font_formula = fm.FontProperties(
math_fontfamily='cm', size=20
)
font_text = {'size': 20}
yticks = [-11, -2.0, -0.5, 0, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0],
colors = '#ff9999'
ylims = [-2000, 1.01]
bar_width = 0.4
frac_b = 1.6
text_skip = 0.03 # 标注的数据与柱状图顶(底)端间距
fig, ax = plt.subplots(tight_layout=True)
ax.bar(x, data[:, ind + 1], facecolor=colors[ind], width=bar_width)
ax.set_xticks(x)
ax.set_xlabel('Model No.', labelpad=18, fontdict=font_text)
ax.set_ylabel(r'$R^2$', fontproperties=font_formula)
ax.set_yscale('function', functions=(forward, inverse))
ax.yaxis.set_minor_formatter(NullFormatter())
ax.yaxis.set_major_locator(FixedLocator(yticks[ind]))
ax.set_ylim(ylims[ind])
# 标注数据
for i in range(14):
cur_r2 = data[i, ind + 1]
cur_skip = frac_b - cur_r2 - 1 / (text_skip + 1 / (frac_b - cur_r2)) # 实际间距与图上间距转换
if cur_r2 > 0:
ax.text(x[i], cur_r2 + cur_skip, f'{cur_r2:.4}', ha='center')
elif cur_r2 == 0:
ax.text(x[i], cur_r2 + cur_skip, 'Divergence' if i == 8 else 'Unfitted', ha='center')
else:
ax.text(x[i], cur_r2 - cur_skip, f'{cur_r2:.4}', ha='center', va='top')
fig.set_size_inches([15.36, 7.57])

数据标注
上方代码的数据标注部分需要额外讲解一下。根据理论部分,实际中的
x
x
x (也即刻度值),在图上表现为
1
/
(
b
?
x
)
1/(b-x)
1/(b?x),我现在想让每个数据都在图上距离bar的顶(底)端0.03个距离。但是我python中代码给的应该是实际距离,怎么办呢?这便是第44行代码(cur_skip=...)的作用。

假设我的bar高度是0.2,现在它顶部的刻度值就是0.2了,假如说我想在
0.2
+
Δ
x
0.2+\Delta x
0.2+Δx 的高度(刻度)标注我的数据,那么它图上的间距是多少呢?大约是
f
o
r
w
a
r
d
(
0.2
+
Δ
x
)
?
f
o
r
w
a
r
d
(
0.2
)
=
1
1.6
?
(
0.2
+
Δ
x
)
?
1
1.6
?
0.2
\mathrm{forward}(0.2+\Delta x) - \mathrm{forward}(0.2)=\frac{1}{1.6-(0.2+\Delta x)}-\frac{1}{1.6-0.2}
forward(0.2+Δx)?forward(0.2)=1.6?(0.2+Δx)1??1.6?0.21?
从这个式子可以很明显看出来,如果bar不是高0.2了,但
Δ
x
\Delta x
Δx 不变,那图上距离就会变了!
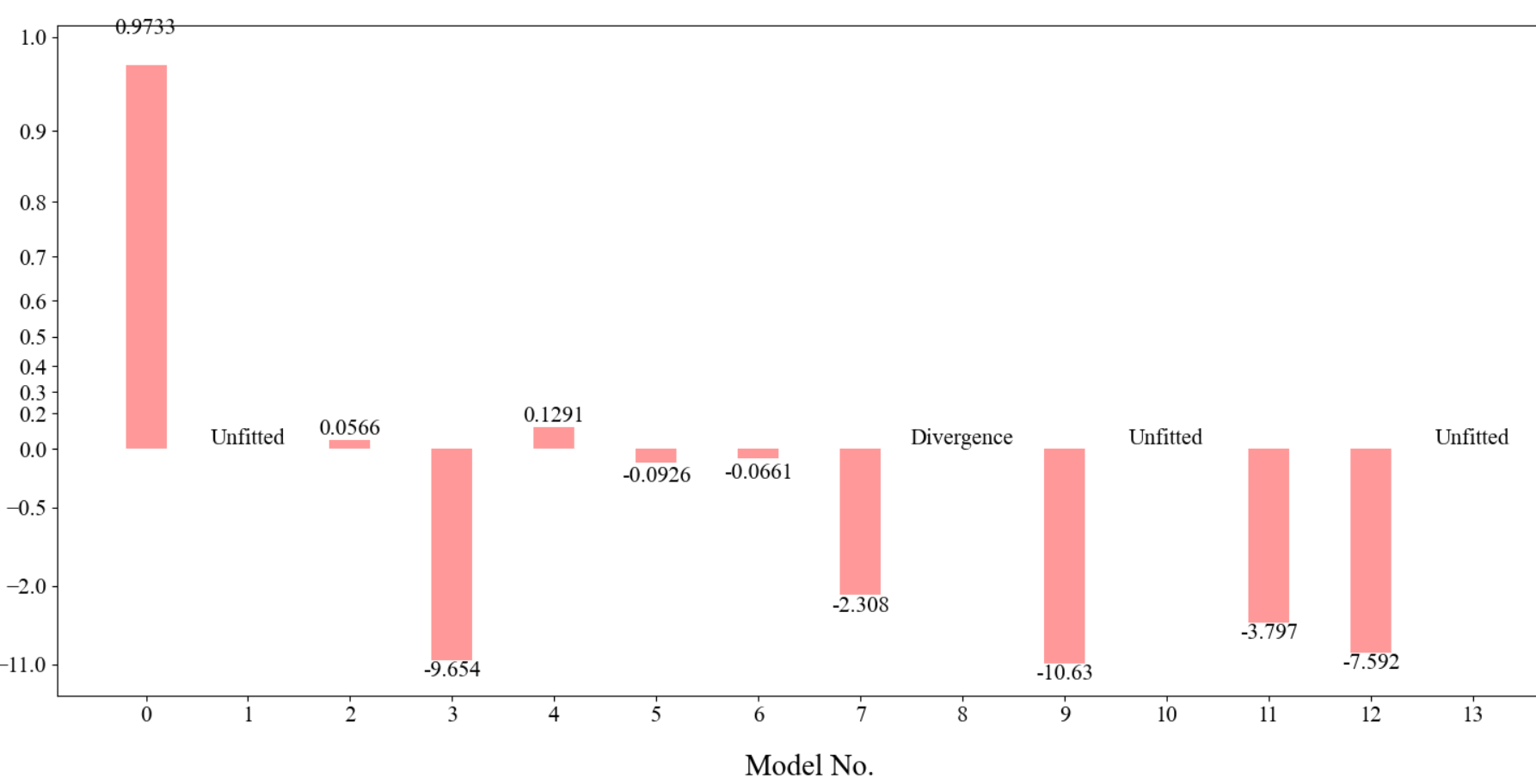
可以看到0.9733距离bar太远了,负值则距离bar太近了,因此必须根据bar的高度动态调整实际间距(
Δ
x
\Delta x
Δx ,代码中为cur_skip),使得每个bar对应的图上间距(
Δ
y
\Delta y
Δy,代码中为text_skip)相同。将式(3)一般化,有
f
o
r
w
a
r
d
(
x
+
Δ
x
)
?
f
o
r
w
a
r
d
(
x
)
=
1
b
?
(
x
+
Δ
x
)
?
1
b
?
x
=
Δ
y
\mathrm{forward}(x+\Delta x) - \mathrm{forward}(x)=\frac{1}{b-(x+\Delta x)}-\frac{1}{b-x}=\Delta y
forward(x+Δx)?forward(x)=b?(x+Δx)1??b?x1?=Δy
用给定的
Δ
y
\Delta y
Δy 表示未知的
Δ
x
\Delta x
Δx,有
Δ
x
=
(
b
?
x
)
?
1
Δ
y
+
1
b
?
x
\Delta x=(b-x)-\frac{1}{\Delta y + \dfrac{1}{b-x}}
Δx=(b?x)?Δy+b?x1?1?
这就是第44行代码的出处。
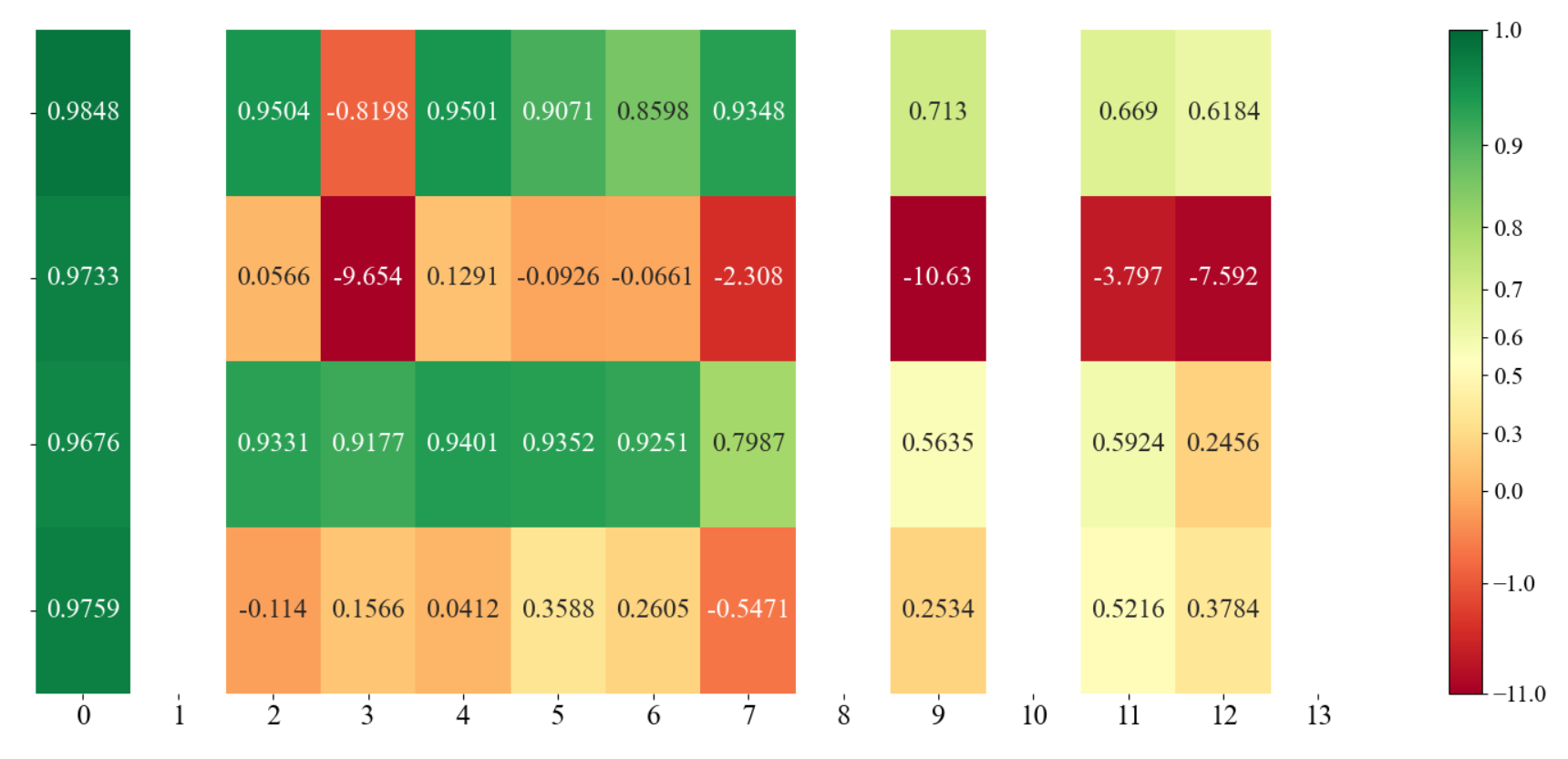
多组数据使用heatmap:自定义color bar的scale
现在我有不止一组数据集,而是四组。当然了可以画四个bar plot,但是我们也可以集成四张bar plot于一张heatmap中:
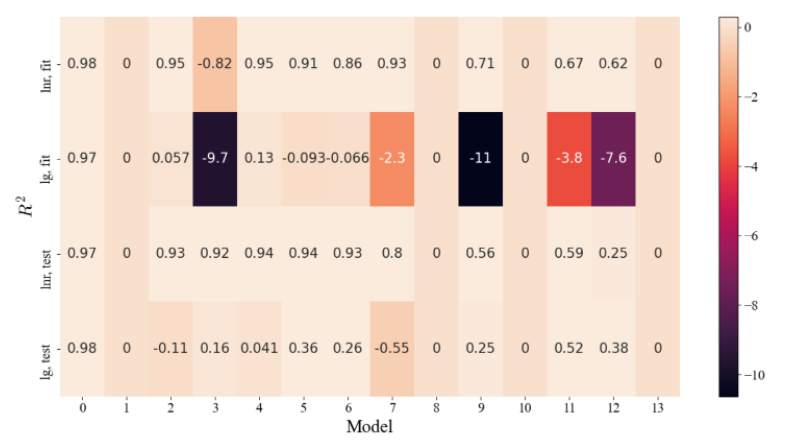
显然,这个也涉及了负数太负使得小的正数无法分辨的问题,需要自定义一下color bar。
原理跟之前一样;代码上,可以使用colors.FuncNorm 这个类(19-22行),vmin 和 vmax 分别指定color bar的下限和上限。
import seaborn as sns
import numpy as np
from matplotlib import pyplot as plt, font_manager as fm, colors
def forward(x):
x = 1 / (frac_b - x)
return x
def inverse(x):
x = frac_b - 1 / x
return x
def comp_heatmap(ax):
plt.rc('font', family='Times New Roman', size=15)
plt.subplots_adjust(left=0.05, right=1)
norm = colors.FuncNorm(
(forward, inverse),
vmin=-11, vmax=1
)
mask = np.zeros_like(data)
mask[:, [1, 8, 10, 13]] = 1
mask = mask.astype(np.bool)
with sns.axes_style('white'):
ax = sns.heatmap(
data, ax=ax, vmax=.3,
mask=mask,
annot=True, fmt='.4',
annot_kws=font_annot,
norm=norm,
xticklabels=np.arange(14),
yticklabels=np.arange(4),
cbar=False,
cmap='RdYlGn'
)
cbar = ax.figure.colorbar(ax.collections[0])
cbar.set_ticks([-11, -1.0, 0, 0.3, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0])
# set tick labels
xticks = ax.get_xticks()
ax.set_xticks(xticks)
ax.set_xticklabels(xticks.astype(int), **font_tick)
yticks = ax.get_yticks()
ax.set_yticks(yticks)
ax.set_yticklabels(['', '', '', ''])
return ax
font_formula = fm.FontProperties(
math_fontfamily='cm', size=22
)
font_text = {'size': 22, 'fontfamily': 'Times New Roman'}
font_annot = {'size': 17, 'fontfamily': 'Times New Roman'}
font_tick = {'size': 18, 'fontfamily': 'Times New Roman'}
fig, axes = plt.subplots()
data = np.array([[ 0.9848, 0. , 0.9504, -0.8198, 0.9501, 0.9071,
0.8598, 0.9348, 0. , 0.713 , 0. , 0.669 ,
0.6184, 0. ],
[ 0.9733, 0. , 0.0566, -9.654 , 0.1291, -0.0926,
-0.0661, -2.3085, 0. , -10.63 , 0. , -3.797 ,
-7.592 , 0. ],
[ 0.9676, 0. , 0.9331, 0.9177, 0.9401, 0.9352,
0.9251, 0.7987, 0. , 0.5635, 0. , 0.5924,
0.2456, 0. ],
[ 0.9759, 0. , -0.114 , 0.1566, 0.0412, 0.3588,
0.2605, -0.5471, 0. , 0.2534, 0. , 0.5216,
0.3784, 0. ]])
frac_b = 1.5
ax = comp_heatmap(axes)
fig.set_size_inches([15.36, 7.57])