一、二项逻辑回归
1.二项逻辑回归是一个功能,最终输出介于0到1之间的值,为了解决类似于“成功或者失败”,“有或无"这种”非是即否"的问题。
2.逻辑回归是一个把线性回归模型映射为概率的模型,即把实数空间的输出[-∞,+∞]映射到(0,1),从而获取概率。(个人理解:回归的含义——用观察使得认知接近真值的过程,回归本源。)
3.通过画图的方式来直观认识这种映射,我们首先定义一个二元线性回归模型:
y
^
=
θ
1
x
1
+
θ
2
x
2
+
b
i
a
s
,
其
中
y
^
∈
(
?
∞
,
+
∞
)
\hat{y}=\theta_1x_1+\theta_2x_2+bias, 其中\hat{y}∈(-∞,+∞)
y^?=θ1?x1?+θ2?x2?+bias,其中y^?∈(?∞,+∞)
线性回归图:

逻辑回归图:

二、probability和odds的定义
1.probability指的是 发生的次数/总次数 ,以抛硬币为例:

p的取值范围为[0,+∞)
2.odds则是一种比率,是指某事件发生的可能性(概率)与不发生的可能性(概率)之比。即 发生的次数/没有发生的次数 ,以抛硬币为例:

odds的取值范围为[0,+∞)
3.回顾伯努利分布:如果X是伯努利分布中的随机变量,X的取值为{0,1},非0即1,如抛硬币的正反面:
则:P(X=1)=p,P(X=0)=1-p
代入odds:
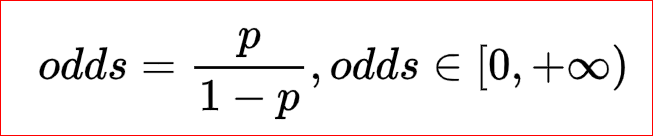
三、logit函数和sigmoid函数及他们的特性:
1.Odds的对数称之为Logit,也写作log-it。
2.我们对odds取log,扩展odds的取值范围到实数空间[-∞,+∞],这就是logit函数:
l
o
g
i
t
(
p
)
=
l
o
g
e
(
o
d
d
s
)
=
l
o
g
e
(
p
1
?
p
)
,
p
∈
(
0
,
1
)
,
l
o
g
i
t
(
p
)
∈
(
?
∞
,
+
∞
)
logit(p)=log_e(odds)=log_e(\frac{p}{1-p}),p∈(0,1),logit(p)∈(-∞,+∞)
logit(p)=loge?(odds)=loge?(1?pp?),p∈(0,1),logit(p)∈(?∞,+∞)
3.我们可以使用线性回归模型来表示logit§,因为线性回归模型和logit函数的输出有着同样的取值范围:
例如:
l
o
g
i
t
(
p
)
=
θ
1
x
1
+
θ
2
x
2
+
b
i
a
s
logit(p)=\theta_1x_1+\theta_2x_2+bias
logit(p)=θ1?x1?+θ2?x2?+bias
以下是logit§的函数图像,注意p∈(0,1),当p=0或者p=1时,logit属于未定义。

由
l
o
g
i
t
(
p
)
=
θ
1
x
1
+
θ
2
x
2
+
b
i
a
s
logit(p)=\theta_1x_1+\theta_2x_2+bias
logit(p)=θ1?x1?+θ2?x2?+bias
得
l
o
g
(
p
1
?
p
)
=
θ
1
x
1
+
θ
2
x
2
+
b
i
a
s
log(\frac{p}{1-p} )=\theta_1x_1+\theta_2x_2+bias
log(1?pp?)=θ1?x1?+θ2?x2?+bias
注:可能有人会产生误解,不理解如何转换,logit§表示的是与参数p相关的对数函数,在这里
logit( p )=log(p/(1-p))。
设
z
=
θ
1
x
1
+
θ
2
x
2
+
b
i
a
s
z=\theta_1x_1+\theta_2x_2+bias
z=θ1?x1?+θ2?x2?+bias
得
l
o
g
(
p
1
?
p
)
=
z
log(\frac{p}{1-p} )=z
log(1?pp?)=z
等式两边取以e为敌的指数函数:
p
1
?
p
=
e
z
\frac{p}{1-p}=e^{z}
1?pp?=ez
p
=
e
z
(
1
?
p
)
=
e
z
?
e
z
p
p=e^{z}(1-p)=e^{z}-e^{z}p
p=ez(1?p)=ez?ezp
p
(
1
+
e
z
)
=
e
z
p(1+e^z)=e^z
p(1+ez)=ez
p
=
e
z
(
1
+
e
z
)
p=\frac{e^z}{(1+e^z)}
p=(1+ez)ez?
分子分母同时除以
e
z
e^z
ez,得
p
=
1
(
1
+
e
?
z
)
,
p
∈
(
0
,
1
)
p=\frac{1}{(1+e^{-z})} ,p∈(0,1)
p=(1+e?z)1?,p∈(0,1)
经过上面的推导,我们得出了sigmoid函数,最终把线性回归模型输出的实数空间取值映射成为概率了。
s
i
g
m
o
i
d
(
z
)
=
1
1
+
e
?
z
,
p
∈
(
0
,
1
)
sigmoid(z)=\frac{1}{1+e^{-z}} ,p∈(0,1)
sigmoid(z)=1+e?z1?,p∈(0,1)
下面是sigmoid的函数图像,注意sigmoid(z)的取值范围

四、最大似然估计
1.引入假设函数
h
θ
(
X
)
h_\theta(X)
hθ?(X),设
θ
T
X
\theta^TX
θTX为线性回归模型:
θ
T
X
\theta^TX
θTX中,
θ
T
\theta^T
θT和X均为列向量,例如:
θ
T
=
[
b
i
a
s
θ
1
θ
2
]
\theta^T=\begin{bmatrix} bias & \theta_1 &\theta_2 \end{bmatrix}
θT=[bias?θ1??θ2??]
X
=
[
1
x
1
x
2
]
X=\begin{bmatrix} 1 \\ x_1 \\ x_2 \end{bmatrix}
X=???1x1?x2?????
求矩阵点积,得出:
θ
T
X
=
b
i
a
s
?
1
+
θ
1
?
x
1
+
θ
2
?
x
2
=
θ
1
x
1
+
θ
2
?
x
2
+
b
i
a
s
\theta^TX=bias*1+\theta_1*x_1+\theta_2*x_2=\theta_1x_1+\theta_2*x_2+bias
θTX=bias?1+θ1??x1?+θ2??x2?=θ1?x1?+θ2??x2?+bias
设
θ
T
X
=
z
\theta^TX=z
θTX=z,则有假设函数:
h
θ
(
X
)
=
1
1
+
e
?
z
=
P
(
Y
=
1
∣
X
;
θ
)
h_\theta (X)=\frac{1}{1+e^{-z}} =P(Y=1|X;\theta )
hθ?(X)=1+e?z1?=P(Y=1∣X;θ)
上式表示的是在条件X和
θ
\theta
θ下Y=1的概率;
P
(
Y
=
1
∣
X
;
θ
)
=
1
?
h
θ
(
X
)
P(Y=1|X;\theta )=1-h_\theta(X)
P(Y=1∣X;θ)=1?hθ?(X)
上式表示的是在条件X和
θ
\theta
θ下Y=1=0的概率。
2.回顾伯努利分布
f
(
k
;
p
)
{
p
,
i
f
k
=
1
q
=
1
?
p
,
i
f
k
=
0
f(k;p)\left\{\begin{matrix} p, &if&k=1 \\ q=1-p, &if&k=0 \end{matrix}\right.
f(k;p){p,q=1?p,?ifif?k=1k=0?
或者
f
(
k
;
p
)
=
p
k
(
1
?
p
)
1
?
k
f(k;p)=p^k(1-p)^{1-k}
f(k;p)=pk(1?p)1?k,for k∈{0,1}。注意f(k;p)表示的是k为0或1的概率,也就是P(k)
3.最大似然估计得目的是找到一个最符合数据的概率分布。
例如下图中的XX指的是数据点,图中所有红色箭头长度的乘积就是似然函数的输出,显然,上半图的分布似然函数要比下半图的大,所以上半图的分布更符合数据,而最大似然估计就是找到一个最符合当前数据的分布。


4.定义似然函数
L
(
θ
∣
x
)
=
P
(
Y
∣
X
;
θ
)
=
∏
i
m
P
(
y
i
∣
x
i
;
θ
)
=
∏
i
m
h
θ
(
x
i
)
y
i
(
1
?
h
θ
(
x
i
)
)
(
1
?
y
i
)
L(\theta|x)=P(Y|X;\theta )=\prod_{i}^{m} P(y_i|x_i;\theta )=\prod_{i}^{m} h_\theta(x_i)^{y_i}(1-h_\theta(x_i))^{(1-{y_i})}
L(θ∣x)=P(Y∣X;θ)=i∏m?P(yi?∣xi?;θ)=i∏m?hθ?(xi?)yi?(1?hθ?(xi?))(1?yi?),
其中i为每个数据样本,共有m个数据样本,最大似然估计的目的是让上式的“从输出值”尽可能大;对上式取log,以方便计算,因为log可以把乘积转换为加法,而且不影响我们的优化目标:
L
(
θ
∣
x
)
=
l
o
g
(
P
(
Y
∣
X
;
θ
)
)
=
∑
i
=
1
m
y
i
l
o
g
(
h
θ
(
x
i
)
)
+
(
1
?
y
i
)
l
o
g
(
1
?
h
θ
(
x
i
)
)
L(\theta|x)=log(P(Y|X;\theta ))=\sum_{i=1}^{m} y_ilog(h_\theta (x_i))+(1-y_i)log(1-h_\theta (x_i))
L(θ∣x)=log(P(Y∣X;θ))=i=1∑m?yi?log(hθ?(xi?))+(1?yi?)log(1?hθ?(xi?))
我们只要在式子前面加一个负号,即可把求最大转化为求最小,设
h
θ
(
X
)
=
Y
^
h_\theta (X)=\hat{Y}
hθ?(X)=Y^,得出损失函数
J
(
θ
)
J(\theta)
J(θ),我们只要最小化这个函数,就能通过求导来得到我们想要的
θ
\theta
θ:
J
(
θ
)
=
?
∑
i
m
Y
l
o
g
(
Y
^
)
?
(
1
?
Y
)
l
o
g
(
1
?
Y
^
)
J(\theta)=-\sum_{i}^{m} Ylog(\hat{Y})-(1-Y)log(1-\hat{Y})
J(θ)=?i∑m?Ylog(Y^)?(1?Y)log(1?Y^)
