[人工智能]多信号分类算法（MUSIC）的理解与应用

1 引言

MUSIC算法本质上是对信号进行“正交分解”的过程。一般地，MUSIC算法用于DOA估计，因此本文首先阐述在这种应用场景下对MUSIC算法的相关理解；接着，分析网络上一些仿真代码的不合理性；最后，给出MUSIC在参数估计领域的其他应用。

2 基本算法流程（一维）与代码（搜索版本，非快速运算）

假设线阵有$M$个阵元，某时刻$t$各个阵元接收到的复信号组成一个“快拍”，记为$\mathbf{y}(t)\in {\mathbb{C}}^M$，则$N$个快拍的接收信号可以表示为$\mathbf{Y}\in {\mathbb{C}}^{M\times N}$，且$\mathbf{Y}=\left[\mathbf{y}(\frac{1}{f_s}),?,\mathbf{y}(\frac{N}{f_s})\right]$。其中，$f_s$为A/D的采样率。
MUSIC算法可以简单地划分为以下三个步骤：
a ) 估计快拍自相关，进而分析信号的“空间相关性”（一般用“平均值”近似“均值”）：
$$\mathbf{R}=E\left[\mathbf{y}{\mathbf{y}}^H\right]\approx \hat{\mathbf{R}}=\frac{\mathbf{Y}{\mathbf{Y}}^H}{N}$$
b ) 自相关矩阵的特征值分解：
$$\begin{array}{rl}\hat{\mathbf{R}}\mathbf{U}& =\mathbf{U}\mathbf{\Lambda }\\ \mathbf{\Lambda }& =\text{diag}\left[{\lambda }_1,?,{\lambda }_M\right]\\ \mathbf{U}& =\left[{\mathbf{u}}_1,?,{\mathbf{u}}_M\right]\end{array}$$
其中，${\lambda }_i$为特征值，${\mathbf{u}}_i$为与之对应的特征向量。假设存在$K$个“时间不相关”且“空间不相关”的信号，则提取$M?K$个小特征值对应的特征向量，组成噪声子空间${\mathbf{U}}_n$。
c ) 搜索：
生成理想的信号快拍$\mathbf{a}(\theta )\in {\mathbb{C}}^M$, 则MUSIC输出可以表示为：
$$P_{MUSIC}(\theta )=\frac{1}{{\mathbf{a}}^H(\theta ){\mathbf{U}}_n{\mathbf{U}}_n^H\mathbf{a}(\theta )}$$

代码，其中$\mathbf{A}=\left[\mathbf{a}({\theta }_1),?,\mathbf{a}({\theta }_L)\right]$：

function Pmusic = MUSIC(Y, K, A)
% size(Y) = [M, N]
N = size(Y, 2);

% step1:
R = (Y * Y') / N;

% step2:
[U, D] = eig(R);
[~, idx] = sort(diag(D), 'descend');
U = U(:,idx);
Un = U(:,K+1:end);

% step3:
Pmusic = zeros(size(A, 2));
for ii = 1:size(A, 2)
    a = A(:,ii);
    Pmusic(ii) = 1 / ( a' * (Un * Un') * a);
end
end

3 空间存在正交分量且时间存在正交分量的信号才能超分辨！！！

注：存在正交分量指两个向量在向量空间中指向的方向存在正交分量，也即这两个向量组成的矩阵是列满秩的。
截至发文时，MUSIC相关文章中最热的文章为《较为详细的MUSIC算法原理及MATLAB实现》 。在该文章中，存在一处仿真BUG，即强制设定频率相同的信号在时间轴上是正交的，具体涉及到的代码为：

A=exp(-1i*2*pi*d.'*sin(theta*derad));  %方向矢量
S=randn(M,K);             %信源信号，入射信号
X=A*S;                    %构造接收信号

上述代码中，从方向矢量$A$可以看出$k=\frac{2\pi }{\lambda }=2\pi$，则信号波长$\lambda =1$,频率$f=\frac{c}{\lambda }=3\times 10^8$。空间轴上，由于同频信号入射角度不同，则不同方向的信号存在“正交成分”。而在时间轴上，这些同频信号应该是“相同”的，即$e^{j2\pi ft}$。程序中其强制设置为高斯分布的随机值，使得在时间轴上这些信号存在正交成分，才能实现超分辨。因此，我们将重写一段程序，给出仿真结果，从而验证网上仿真结果的不合理性：
a ) 当$S=\text{randn}(M,K)$时（仿真BUG）

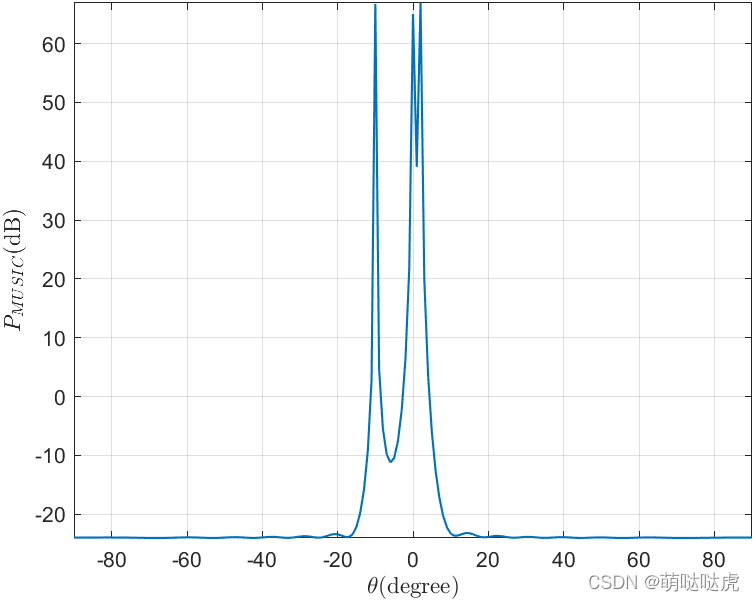
b )当$S=e^{j2\pi f(0:N?1)/fs}$时（实际情况）

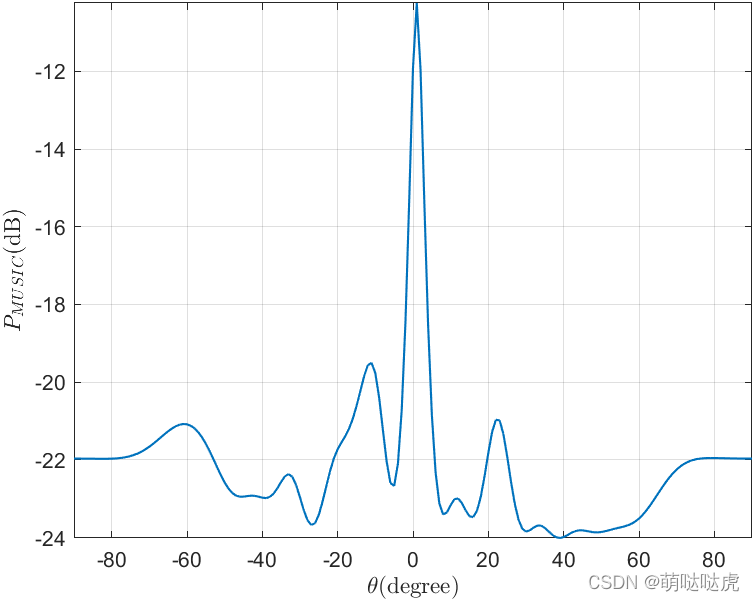
4 结论及原因分析

从上述结果中可知，MUSIC算法对信号在时间维度上的相关性也有要求。在《Music算法详解》 中，也提到了这种现象，产生该现象的原因如下：
在求解自相关矩阵的时候，我们使用时间平均近似集总平均，即认为
$$E\left[\mathbf{y}{\mathbf{y}}^H\right]\approx \frac{\mathbf{Y}{\mathbf{Y}}^H}{N}$$
但由于同频信号在时间维度是完全相同的，因而其在时间维度不能视为“各态历经的平稳随机过程”，而只有各态历经约束情况下，我们才能够认为时间平均能够近似集总平均，这就是MUSIC算法的问题所在。

5 主程序代码

clearvars;
close all;
clc;
%%
M = 16;
N = 200;             
fs = 20e3;
f = 10 * fs / N;           	
lambda = 3e8/f;                  	
search_Azimuth = -90:1:90;
d = 0.5*lambda;
snr = 20;                		
source_doa = [0,2,-10];
K = length(source_doa);
%%
Xm = d*(0:M-1).';         
lambda = 3e8 / f;                  	

A = zeros(M, K);
for q = 1:K
    A(:,q) = exp(-1j*Xm*2*pi*sin(source_doa(q)*pi/180)/lambda);
end

% MK and KN -> MN
noise = (1/sqrt(2)*sqrt(10.^(-snr/10)))*(randn(M,N)+ 1j*randn(M,N));
% s = 1/sqrt(2)*(randn(K, N) + 1j*randn(K,N));	% 仿真bug
s = repmat(exp(1j*2*pi*f*(0:N-1)/fs), K, 1);    % 实际情况
Y = A*s + noise;        % received data

Ax = zeros(M, length(search_Azimuth));
for q = 1:length(search_Azimuth)
    Ax(:,q) = exp(-1j*Xm*2*pi*sin(search_Azimuth(q)*pi/180)/lambda);
end

Pmusic = MUSIC(Y, K, Ax);

figure;
plot(search_Azimuth, db(Pmusic), 'LineWidth', 1);
grid on; axis tight;
xlabel('$\theta$(degree)','Interpreter','latex');

阅读世界，共赴山海

423全民读书节，邀你共读