1 隐马尔可夫模型

概率图模型（probabilistic graphical model）：用图来表达变量相关关系的概率模型。最常见的是用一个结点表示一个或一组随机变量，节点之间的边表示变量间的概率相关关系，即变量关系图。概率图模型大概可以分类为：

有向无环图（有向图模型或贝叶斯网）
无向图（无向图模型或马尔可夫网）

隐马尔可夫模型（HMM）：是结构最简单的动态贝叶斯网，是一种著名的有向图模型。主要应用于时间序列数据建模。隐马尔可夫模型中有两类变量：

状态变量（隐变量）：表示第 $i$ 时刻的系统状态 $\{y_1,y_2,\cdots,y_n\}$ ，一般是隐藏的、不可被观测的。
观测变量： $\{x_1,x_2,\cdots, x_n\}$ ，表示第 $i$ 时刻的观测值。

在隐马尔可夫模型中，系统通常在多个状态 $\{s_1,s_2,\cdots,s_N\}$ 之间转换，因此状态变量 $y_i$ 的取值范围通常是有 $N$ 个可能取值的离散空间，因此状态变量 $y_i$ 的取值范围 $Y$ 通常是有 $N$ 个可能取值的离散空间（ $\subset S$ ）。观测变量可以是离散型也可以是连续型。为便于讨论，我们假定其取值范围 $X=\{o_1,o_2,\cdots,o_M\}$ 。

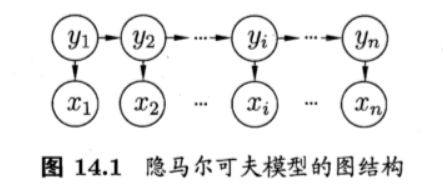
在这里插入图片描述

在任一时刻，观测变量的取值 $x_t$ 仅由状态变量 $y_t$ 确定，与其他状态变量以及观测变量的取值无关。同时 $t$ 时刻的状态 $y_t$ 仅依赖于 $t ? 1$ 时刻的状态 $y_{t-1}$ ，与其余 $n ? 2$ 个状态无关，这就是所谓的 “马尔可夫链”：系统下一时刻的状态仅有当前状态决定，不依赖于以往的任何状态。 所有变量的联合概率分布定义为：
$P(x_1,y_1,\cdots,x_n,y_n)=P(y_1)P(x_1|y_1)\prod_{i=2}^nP(y_i|y_{i-1})P(x_i|y_i)$
除了结构信息，欲确定一个隐马尔可夫模型还需要以下三组参数：

状态转移概率：
$a_{ij}=P(y_{t+1}=s_j|y_t=s_i),\ \ \ \ \ 1\le i,j\le N$
输出观测概率：
$b_{ij}=P(x_t=o_j|y_t=s_i)$
初始状态概率：
$\pi_i=P(y_1=s_i)$

2 马尔可夫随机场

马尔可夫随机场（MRF）：典型的马尔可夫网，是一种著名的无向图模型:

结点：一个或一组变量
边：变量之间的依赖关系

马尔可夫随机场有一组势函数（potential functions），也叫做“因子”，即定义在变量子集上的非负实函数，主要用于定义概率分布函数。

马尔可夫随机场中，对于图中结点的一个子集，如果其中任意两个结点都有边连接，则称该结点子集为一个“团”，若团中再加入一个结点，则无法构成团，则称为“极大团”。

在这里插入图片描述

在马尔可夫随机场中，多个变量之间的联合概率分布能基于团分解为多个因子的乘积，每个因子仅与一个团相关。具体来说，对于 $n$ 个变量 $X=\{x_1,x_2,\cdots, x_n\}$ ，所有团构成的集合为 $C$ ，与团 $Q\in C$ 对应的变量集合记为 $X_Q$ ，则联合概率 $P (X)$ 定义为
$P(X)=\frac{1}{Z}\prod_{Q\in C} \psi(X_Q)$
在马尔可夫随机场中如何得到“条件独立性”呢？同样借助分离的概念。如下图所示，若从结点集A中的结点到B中的结点都必须经过结点集C中的结点，则称结点集A和B被结点集C分离， C称为"分离集" (separating set)。

对马尔可夫随机场，有 “全局马尔可夫性” (global Markov property)：给定两个变量子集的分离集，则这两个变量子集条件独立。也就是说，图中若令 A， B和C对应的变量集分别为 $X_A,X_B, X_C$ ，则 $X_A$ 和 $X_B$ 在给定 $X_C$ 的条件下独立，记为 $XA\perp XB|X_C$ 。

在这里插入图片描述

由全局马尔可夫性，可以得到两个有用的推论：

局部马尔科夫性： 给定某变量的邻接变量，则该变量条件独立于其他变量。
成对马尔可夫性： 给定所有其他变量，两个非邻接变量条件独立。

下面来考察马尔可夫随机场中的势函数，其作用是定量刻画变量集 $X_Q$ 中变量的相关关系 （非负函数），且在所偏好的变量取值上有较大的函数值。

为了满足非负性，指数函数常被定义势函数：
$\psi_Q(X_Q)=e^{-H_Q(X_Q)}$

3 条件随机场

条件随机场(Conditional Random Field，简称 CRF) 是一种判别式无向图模型，是判别式模型。条件随机场试图对多个变量在给定观测值后的条件概率进行建模。

令 $G = (V, E)$ 表示结点与标记变量 $y$ 中元素一一对应的无向图， $y_v$ 表示与结点 $v$ 对应的标记变量， $n (v)$ 表示结点 $v$ 的邻接结点，若图 $G$ 的每个变量 $y_v$ 都满足马尔可夫性，即
$\ { v } ) = P ( y v ∣ x , y n ( v ) ) P(y_v|x,y_{V\backslash \{v\}})=P(y_v|x,y_{n(v)})$
则 $(y, x)$ 构成一个条件随机场。

在这里插入图片描述

4 学习与推断

变量消去

在这里插入图片描述

信念传播

在这里插入图片描述

5 近似推断

MCMC采样：关键在于通过构造"平稳分布为 $p$ 的马尔同夫链" 来产生样本。
变分推断：通过使用己知简单分布来逼近需推断的复杂分布，并通过限制近似分布的类型，从而得到一种局部最优、但具有确定解的近似后验分布。

6 话题模型

话题模型(topic model)是一族生成式有向图模型，主要用于处理离散型的数据(如文本集合)，在信息检索、自然语言处理等领域有广泛应用。隐狄利克雷分配模型(Latent Dirichlet Allocation，简称LDA) 是话题模型的典型代表。

话题模型中的基本概念：

词（word）：最基本离散单元
文档（document）：不计顺序（词袋）
话题（topic）：一系列相关的词，以及它们在该概率下出现的概率

不妨假定数据集中一共包含 $K$ 个话题和 $T$ 篇文档，文档中的词来自一个包含 $N$ 个词的词典。我们用 $T$ 个 $N$ 维向量 $w=\{w_1,w_2,\cdots,w_T\}$ 表示数据集(即文档集合)， $K$ 个 $N$ 维向量 $\beta_k\ \ (k=1 ,2,\cdots, K)$ 表示话题，其中 $w_T\in \mathbb R^N$ 的第 $n$ 个分量 $w_{t,n}$ 表示文档 $t$ 中词 $n$ 的词频， $\beta_k\in \mathbb R^N$ 的第 $n$ 个分量 $\beta_{k,n}$ 表示话题 $k$ 中词 $n$ 的词频。

LDA从生成式模型的角度来看待文档和话题。具体来说，LDA认为每篇文档包含多个话题，不妨用向量 $\theta_t\in \mathbb R^N$ 表示文档 $t$ 中所包含的每个话题的比例， $\theta_{t,k}$ 表示文档 $t$ 中包含话题 $k$ 的比例，进而通过下面的步骤由话题"生成"文档 $t$ ：