[人工智能]RNN、GRU和LSTM的结构与公式讲解

本文基于吴恩达的视频和符号规定，对RNN/GRU/LSTM的结构和公式进行介绍，重点解释了RNN的前向和反向传播过程，尤其是RNN的反向传播自认为讲得还比较容易理解。个人的一点经验，这部分泛泛地看是比较难看懂的，可以跟着一个老师或者讲得比较清楚的帖子，仔细啃一遍。

[ 一 ] RNN的简要介绍

首先，为什么需要RNN这种新的结构呢？

它与以往的多层感知机和卷积神经网络的最大不同点在于：它是一种序列模型，隐藏层之间的节点不再无连接而是有连接的，并且隐藏层的输入不仅包括输入层的输出还包括上一时刻隐藏层的输出。

对于MLP或CNN，给一些训练数据，这些数据是彼此独立的，互不相关的，但是现实中一些与时间先后有关的, 比如视频的下一时刻的预测，文档前后文内容的预测等， 这些算法的表现就不尽如人意了，而RNN这种串联的网络结构非常适合于时间序列数据，可以保持数据中的依赖关系。

RNN的一般结构如何？

下图是RNN的一般结构，右边是按时间展开，通过隐藏层上的连接，使得前一时刻的网络状态能够传递给当前时刻，当前时刻的状态也可以传递给下个时刻。

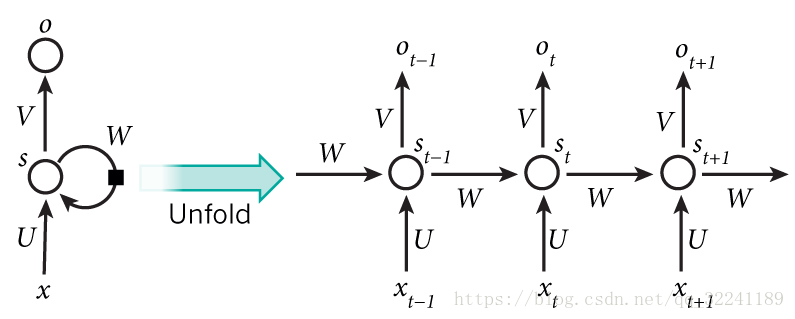
[ 二 ] RNN的前向传播

RNN的网络结构这里，我将采用吴恩达课程中的符号体系，这部分的网络资源，我个人觉得李宏毅可以从整体角度让人理解RNN是用来干什么的，直观的理解它的一些思想，吴恩达讲的比较细节，会从结构和推导进行深入讲解，李沐更倾向于是简单介绍，但好处是会讲代码和答疑。

从简单的情况开始，假设只有一个隐藏层，且输入序列长度等于输出序列。

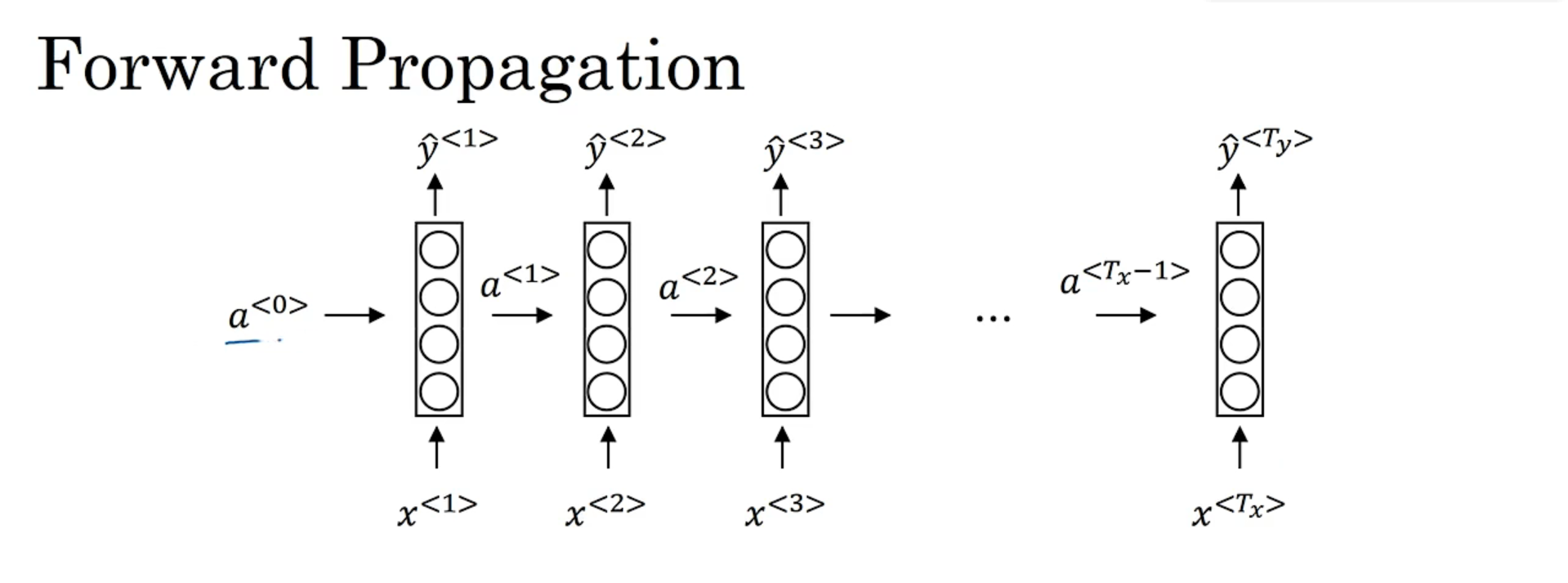
$x^{<1>},...,x^{<9>}$ 是输入序列，$x^{<i>}$是一个向量，上标 $i$ 代表第 $i$ 个时间步，$a^{<t>}$ 表示隐层的输出，方框里面一个个圆圈代表隐层。（可以也可以看出，同一层的结点之间是有连接的，和普通的全连接网络不同，普通全连接网络只有层与层之间的连接）

进行前向传播时，首先由$x^{<1>}$ 计算 $a^{<1>}$ ，计算式为：$$a^{<1>}=g(W_{aa}{a}^{<0>}+W_{ax}{x}^{<1>}+b_a)$$ 根据这个式子，可以看出，计算第 $i$ 个时间步的 $a^{<i>}$用到了第 $i$ 个时间步的输入 $x^{<i>}$ 和上一个时间步的记忆 $a^{<i?1>}$ ，此处是第一个时间步了， $a^{<0>}$ 哪里来呢？一般就是用一个全 0 向量来代替。 如果式子中没有 $W_{aa}{a}^{<i>}$ 部分，那就和多层感知机的结构一样了。这里的激活函数一般使用 tanh 或 relu.

由 $a^{<1>}$ 计算 ${\hat{y}}^{<1>}$的表达式如下：$${\hat{y}}^{<1>}=g(W_{ya}{a}^{<1>}+b_y)$$ 此处的激活函数要根据具体的任务来定，如果是二分类，一般用 sigmoid，如果是多分类，一般用 softmax.

同样的，接着开始计算 $a^{<2>}$ 和 ${\hat{y}}^{<2>}$，对于更一般的情况，即，计算 $a^{<t>}$ 和 ${\hat{y}}^{<t>}$ 的表达式为：$$a^{<t>}=g(W_{aa}{a}^{<t?1>}+W_{ax}{x}^{<t>}+b_a)$$ $${\hat{y}}^{<t>}=g(W_{ya}{a}^{<t>}+b_y)$$ 对于每一步的计算来说，$W_{aa}$都是同样的，$W_{ya}，b_a，b_y$ 也是同样的，对所有时间步来说都是共享的参数。

吴恩达的视频中介绍了对这里的式子的简化。将 $$a^{<t>}=g(W_{aa}{a}^{<t?1>}+W_{ax}{x}^{<t>}+b_a)$$ 改写为$$a^{<t>}=g(W_a[a^{<t?1>},x^{<t>}]+b_a)$$ $W_a$ 是将 $W_{aa}$ 和 $W_{ax}$ 左右粘起来，举个例子来进行理解：

假设 $x^{<t>}$是1000维的向量，$a^{<t?1>}$是100维的向量，那么 $W_{aa}$ 是100×100的矩阵，$W_{ax}$ 是100×1000的矩阵。

简化后$a^{<t?1>}$和$x^{<t>}$拼在一起成为 1100维向量，$W_a$ 是100 ×1100 的矩阵，这样写比较简便，而且与原来的运算结果完全一样。

在介绍反向传播之前，先定义一下损失函数，使用交叉熵损失函数：$$L^{<t>}({\hat{y}}^{<t>},y^{<t>})=?y^{<t>}log{\hat{y}}^{<t>}?(1?y^{<t>})log(1?{\hat{y}}^{<t>})$$这是第 t 个时间步上的损失，整个序列的损失就是将 t 个损失进行求和。

[ 三 ] RNN的反向传播BPTT

RNN的反向传播叫做 Backpropagation through time（BPTT），即通过时间反向传播，即从最后一个时间步逐个传向前面的时间步，和普通的神经网络一样重复地使用链式法则。为了方便，下面的推导都把上标${}^{<t>}$ 写为下标 ${}_t$

首先是输出层参数$W_{ya}$，先要定义${\beta }_t=W_{ya}{a}_t$ ，代表隐层乘权重矩阵到输出层，但还没有经过激活函数的状态 ( 这里先忽略偏置项，其实有没有都一样，后面求导是不影响的)： $$\frac{?L_t}{?W_{ya}}=\frac{?L_t}{?{\hat{y}}_t}\frac{?{\hat{y}}_t}{?W_{ya}}=\frac{?L_t}{?{\hat{y}}_t}\frac{?{\hat{y}}_t}{?{\beta }_t}\frac{?{\beta }_t}{?W_{ya}}$$
然后是 $W_{aa}$ 和 $W_{ax}$，这两个在更新梯度时都需要考虑当前时刻的梯度（当前时刻 t 的损失函数传下来的梯度）和下一时刻的梯度（从 t+1时刻传下来的梯度），为了表示方便，再定义两个变量：$z_t=W_{ax}{x}_t+W_{aa}{a}_{t?1}$，就是第 t 个时间步的隐层结点（接受了 t 时刻的输入$x_t$和 t-1 时刻的$a_{t?1}$) 但还没有经过激活函数。令 ${\delta }_t$ 表示 t 时刻 $z_t$ 接受到的梯度。$${\delta }_t=\frac{?L_t}{?\widehat{y_t}}\frac{?\widehat{y_t}}{?a_t}\frac{?a_t}{?z_t}+{\delta }_{t+1}\frac{?z_{t+1}}{?a_t}\frac{?a_t}{?z_t}$$ 求出 ${\delta }_t$ 后，可以很容易地求 $L_t$ 对$W_{aa}$ 和 $W_{ax}$ 的导数：${\delta }_t{a}_{t?1}^T，{\delta }_t{x}_t^T$

举个具体的小例子看看究竟怎么算，假设一共只有三个时间步，数据的前向传播过程如下 (这里$z，\beta$ 带了偏置项，不过不影响)：

$W_{ya}$ 的梯度就不算了因为比较简单。首先看第三个时间步，看 $L_3$ 对 $W_{aa}$ 的影响：$$\frac{?L_3}{?W_{aa}}=\frac{?L_3}{?\widehat{y_3}}\frac{?\widehat{y_3}}{?{\beta }_3}\frac{?{\beta }_3}{?a_3}\frac{?a_3}{?z_3}\frac{?z_3}{?W_{aa}}$$ 等号右边除掉最后一项 $\frac{?z_3}{?W_{aa}}$ 就是我们上面规定的 ${\delta }_3$，之所以规定这个是为了计算和描述方便，因为漏掉的这一项后面还要进行展开。

梯度往回传，来到第二个时间步，不仅要考虑 由 $L_2$ 计算来的梯度，还有 t=3时刻传来的梯度。首先考虑 $L_2$ 的：$$\frac{?L_2}{?W_{aa}}=\frac{?L_2}{?\widehat{y_2}}\frac{?\widehat{y_2}}{?{\beta }_2}\frac{?{\beta }_2}{?a_2}\frac{?a_2}{?z_2}\frac{?z_2}{?W_{aa}}$$然后是$L_3$ 经 $a_3$ 传到 $a_2$ 这里的，其实就是上面的$\frac{?L_3}{?W_{aa}}$ 继续往下链式求导：$$\frac{?L_3}{?\widehat{y_3}}\frac{?\widehat{y_3}}{?{\beta }_3}\frac{?{\beta }_3}{?a_3}\frac{?a_3}{?z_3}\frac{?z_3}{?a_2}\frac{?a_2}{?z_2}\frac{?z_2}{W_{aa}}={\delta }_3\frac{?z_3}{?a_2}\frac{?a_2}{?z_2}\frac{?z_2}{W_{aa}}$$ 所以第2个时间步接受的总的梯度是二者相加。

来到第一个时间步，图上虽然没画，但实际上有个 $a_0$。 最终对 $W_{aa}$ 的更新就是 $L_3$ 传来的梯度+ $L_2$ 传来的梯度+ $L_1$ 传来的梯度.

对 $W_{ax}$ 的计算也是同样的道理，就不再多说了，本质上依然是链式求导一直传下去。或者这么说，把 $L_t$ 当做是 待更新参数如 $W_{aa}$ 的多层嵌套的复合函数，用链式法则一直求导到最里层的我们的待更新参数，一层层剥开的那种感觉。

[ 四 ] RNN 的梯度消失和梯度爆炸

梯度消失 是指很多导数连乘的结果会非常接近于0，梯度消失使得RNN不善于捕获长距离依赖。如说一个很深很深的网络，对这个网络从左到右做前向传播然后再反向传播，从输出 $\hat{y}$ 得到的梯度很难传播回去，很难影响靠前层的权重，很难影响前面层的计算。一个输出主要与附近的输入有关，基本上很难受到序列靠前的输入的影响，这是因为不管输出是什么，不管是对的，还是错的，这个区域都很难反向传播到序列的前面部分，也因此网络很难调整序列前面的计算。这是基本的RNN算法的一个缺点。

梯度消失在训练RNN时是首要的问题，尽管梯度爆炸也是会出现，但是梯度爆炸很明显，因为指数级大的梯度会让你的参数变得极其大，以至于你的网络参数崩溃。所以梯度爆炸很容易发现，因为参数会大到崩溃，你会看到很多NaN，或者不是数字的情况，这意味着你的网络计算出现了数值溢出。如果你发现了梯度爆炸的问题，一个解决方法就是用梯度修剪。梯度修剪的意思就是观察你的梯度向量，如果它大于某个阈值，缩放梯度向量，保证它不会太大，这就是通过一些最大值来修剪的方法(也就是当你计算的梯度超过阈值c或者小于阈值-c的时候，便把此时的梯度设置成c或-c)。

[ 五 ] 门控循环单元GRU

GRU改变了RNN的隐藏层，使其可以更好地捕捉深层连接，并改善了梯度消失问题这是视频中给出的GRU公式，然后我来细细讲一下：

（1）首先，原来的 $a^{<t>}$ 在此处都用 $c^{<t>}$ 来表示，指的是第 $t$ 个时间步的隐层输出值，自然地，$W_a$ 也改为 $W_c$ . $c$ 表示 cell ，理解为“记忆细胞”，就是有记忆能力，可以保持之前的 cell 的值，从而缓解梯度消失/长距离依赖的问题。

（2）除了 $c^{<t>}$ ，还新增了 ${\tilde{c}}^{<t>}$作为候选值。后面可以看到，按原来计算 $a^{<t>}$ 的公式在此处得到的其实是候选值 ${\tilde{c}}^{<t>}$，再经过一些处理才会最终得到 $c^{<t>}$ 。

（3）有两个“门” ，“门”用 $\Gamma$ 表示， $\Gamma$ 外面套得都是sigmoid，其值在 0~1之间，且大概率比较接近0或1，从而实现控制。这两个门分别是：

• ${\Gamma }_r$：相关门，控制 ${\tilde{c}}^{<t>}$ 和 $c^{<t?1>}$ 之间的相关性大小，r 表示relevant
• ${\Gamma }_u$：更新门，控制记忆细胞的值是否更新，即是否用 ${\tilde{c}}^{<t>}$ 更新 $c^{<t>}$ ，u 表示 update

现在，把整个过程理一遍，$c^{<t?1>}$ 是上个时间步的隐层输出，首先由 $c^{<t?1>}$ 和 $x^{<t>}$ 计算出候选值 ${\tilde{c}}^{<t>}$：$${\tilde{c}}^{<t>}=tanh(W_c[{\Gamma }_r?c^{<t?1>}，x^{<t>}]+b_c)$$这个计算出的值本来应该是 RNN中的 $a^{<t>}$（或者此处叫 $c^{<t>}$），但现在它只是候选值了，还要进行一些操作来确定最终的 $c^{<t>}$。注意，这里 $c^{<t?1>}$还乘了一个 ${\Gamma }_r$，如果 ${\Gamma }_r$接近于0，就说明和上一时间步的隐层输出相关性很小，否则就很大。${\Gamma }_r$的值相当于 “门敞开的程度”，控制 $c^{<t?1>}$ 对下一时间步的影响。

然后计算 $c^{<t>}$：$$c^{<t>}={\Gamma }_u?{\tilde{c}}^{<t>}+(1?{\Gamma }_u)?c^{<t?1>}$$如果 ${\Gamma }_u$ 接近于1，那 $c^{<t>}$ 就约等于候选值，如果 ${\Gamma }_u$ 接近于0，那 $c^{<t>}$ 就等于上一时间步的输出，相当于没有进行更新，保持了之前的值，也就类似于“记忆”。

不难看出，RNN 就是 ${\Gamma }_r=1,{\Gamma }_u=1$时的特殊情况下的 GRU。不过我也在想，只有 ${\Gamma }_u$ 行不行？它等于1就更新，等于0就不更新。为什么有 ${\Gamma }_r$？这是因为多年来研究者们试验过很多很多不同可能的方法来设计这些单元，去尝试让神经网络有更深层的连接，去尝试产生更大范围的影响，还有解决梯度消失的问题，GRU就是其中一个研究者们最常使用的版本，也被发现在很多不同的问题上也是非常健壮和实用的。（大概就是因为，这样做在实验中表现就是好？

[ 六 ] 长短期记忆神经网络 LSTM

LSTM是GRU更通用更强大的形式，现在来理一下LSTM的结构。首先是记忆细胞 c ，使用 ${\tilde{c}}^{<t>}=tanh(W_c[a^{<t?1>}，x^{<t>}]+b_c)$ 来更新它的候选值。注意了，在LSTM中我们不再有 $a^{<t>}=c^{<t>}$的情况，现在我们专门使用 $a^{<t>}$ 或者$a^{<t?1>}$，并且也不用 ${\Gamma }_r$，即相关门。

像GRU一样有一个更新门 ${\Gamma }_u$ 和表示更新的参数 $W_u$ ，但是不只有一个更新门控制，④中的 ${\Gamma }_u$ 和 $1?{\Gamma }_u$ 用不同的项来表示，以便形成更灵活的结构。因而，令${\Gamma }_f$ 代替 $1?{\Gamma }_u$ ，${\Gamma }_f$ 表示遗忘门，控制多大程度上忘掉 $c^{<t?1>}$。所以这给了记忆细胞选择权去维持旧的值 $c^{<t?1>}$ 或者就加上新的值${\tilde{c}}^{<t>}$，所以这里用了单独的更新门 ${\Gamma }_u$ 和遗忘门 ${\Gamma }_f$ .

然后还有一个新的输出门 ${\Gamma }_o$ ，将 $a^{<t>}=c^{<t>}$ 变成 $a^{<t>}={\Gamma }_o?c^{<t>}$

我们用图来进行更直观的理解：

由 $a^{<t?1>}$ 和 $x^{<t>}$ 计算出 ${\Gamma }_f,{\Gamma }_u,{\Gamma }_o$ 在 t 时刻的值，以及 ${\tilde{c}}^{<t>}$，然后 $c^{<t?1>}?{\Gamma }_f$，${\tilde{c}}^{<t>}?{\Gamma }_u$ ，二者相加得到 $c^{<t>}$， $c^{<t>}$经过tanh后乘 ${\Gamma }_o$ 得到隐层输出 $a^{<t>}$.

[ 七 ] 比较GRU和LSTM

我们什么时候应该用GRU？什么时候用LSTM？这里没有统一的准则。实际在深度学习的历史上，LSTM更早出现，而GRU是最近才发明出来的，它可能源于Pavia在更加复杂的LSTM模型中做出的简化。

GRU的优点是这是个更加简单的模型，所以更容易创建一个更大的网络，而且它只有两个门，在计算性上也运行得更快，然后它可以扩大模型的规模，而且还效果还不错。

但是LSTM更加强大和灵活，因为它有三个门而不是两个。如果你想选一个使用，我认为LSTM在历史进程上是个更优先的选择，所以如果你必须选一个，我感觉今天大部分的人还是会把LSTM作为默认的选择来尝试。

[ 八 ] 总结

RNN是一种序列模型，常用来进行命名实体识别，机器翻译，文本生成等任务。它的典型特点就是某一时刻隐层的输出不仅与该时刻的输入数据有关，还与上一时刻的隐层输出有关，但是RNN有梯度消失和长期依赖的问题。GRU在RNN的基础上加了两个门：相关门与更新门，GRU可以形成记忆并在每一时刻决定是否更新，RNN可以看作是GRU的特殊情况。而LSTM则是更强大和通用的版本。

阅读世界，共赴山海

423全民读书节，邀你共读