一元线性回归
仍以预测房价的数据集为例,
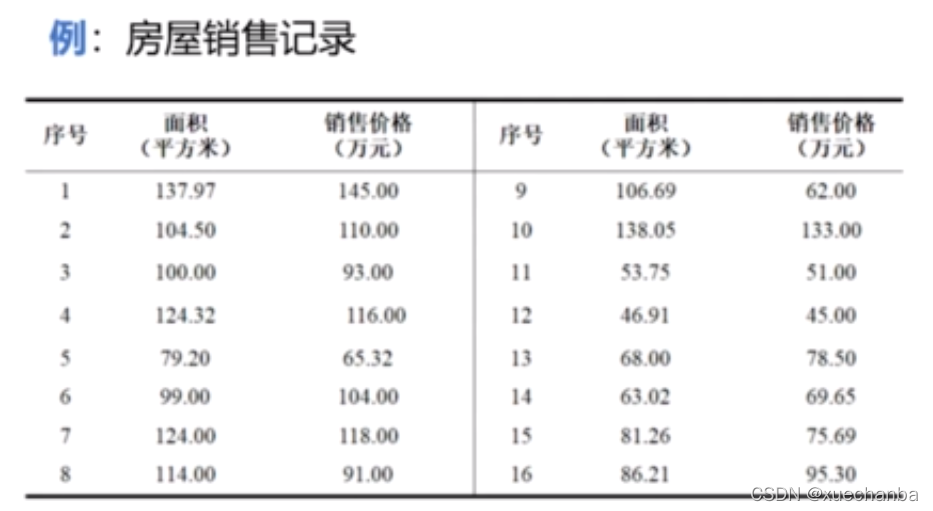
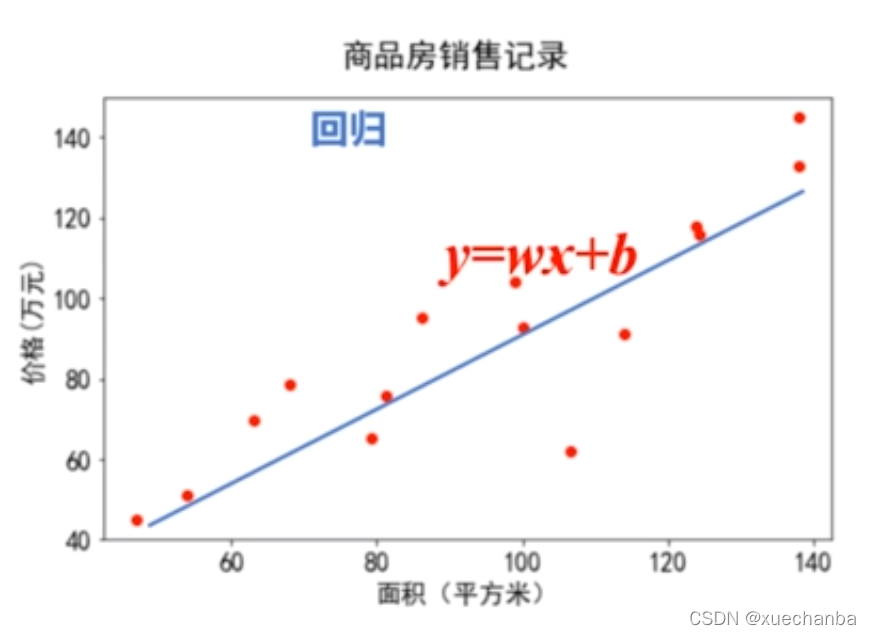
通过观察样本数据集,根据面积和销售价格的关系,可以近似的用一条直线来表示。只要找到这条直线,就可以根据任何一个给定面积,估计出合理的房价。这是一个典型的回归问题。因为回归主要用于预测数值型数
据。即根据观测到的数据设计一种模型,描述数据之间蕴含的关系。
回归的典型例子就是通过给定的数据点,拟合出最优的曲线。在这个例子中,面积和房价之间的关系,可以近似的表示成一个直线。因此,这种模型又被称之为线性回归模型。在这种线性回归模型中,只包含一个自变量x,因此这种线性回归模型又被称之为一元线性回归。

那怎么根据样本(x,y)来确定模型参数 w 和 b 呢?
假设有n组样本,下标 i 为样本的序号。xi是样本属性,例如房屋面积。yi是样本标记,比如房屋的价格。
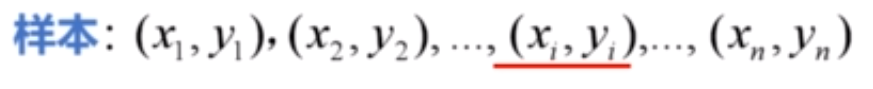
对于平面中的n个点,可以有无数条直线来拟合它们。
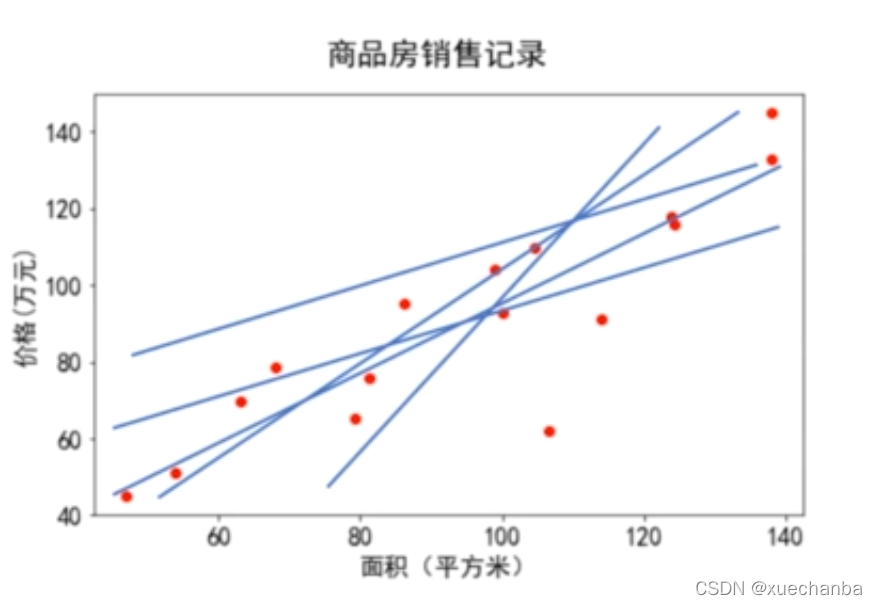
那么,哪条直线拟合的最好呢?
假设下图中的直线是其中一条拟合直线,这条直线上的值称为估计值。
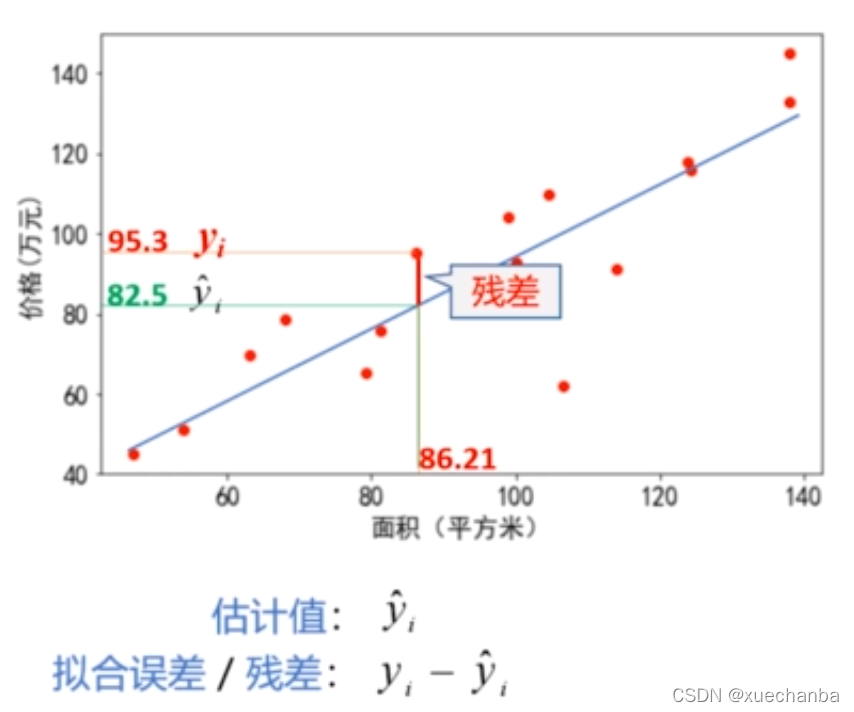
估计值用公式表示为:
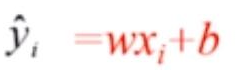
将其代入拟合误差公式:
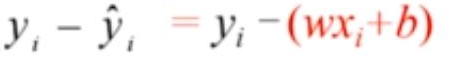
综合所有的样本点来看,最佳拟合直线应该使得所有样本总的拟合误差达到最小。也就是说,最佳拟合直线应该使得所有点的残差累计值最小。
那怎样才能使得所有点的残差累计值达到最小呢?
首先,所有点的残差进行相加,其中,第i个点的残差为:
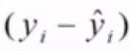
因此所有点的残差和为:
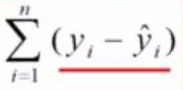
也被定义为损失函数loss。

这个Loss函数也被称之为损失函数或者代价函数,用来评估模型的预测值和真实值的不一致程度。
通过观察这个值:
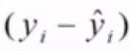
可以发现,残差值是有符号的。在这条直线上方的点,它的残差值总是为正,而下方的点,它的残差值总是为负。如果将残差简单的相加,那么正的残差值和负的残差值就会相互抵消,这样做的话,有可能每个样本单独的残差都很大,而计算得到的残差的累计和却很小。这样的直线显然不满足我们的预期,因此,损失函数的值应该是一个非负的数,那么我们很容易想到可以使用绝对值来消除残差中符号的影响。
使用残差绝对值的和作为损失函数,可以避免正负误差相互抵消的问题。

但是,求残差和最小是一个求最值的问题,在求函数的最值时,一般要进行求导运算。而绝对值是不利于求导运算的,为了消除绝对值运算,可以将这个公式中的绝对值改为平方,使得所有样本点的残差平方和最小。
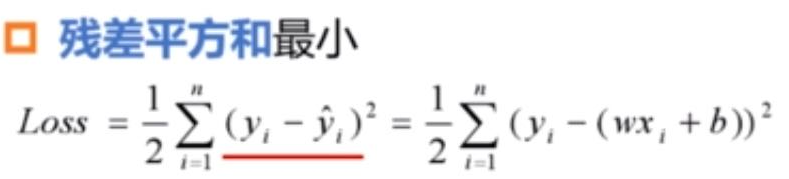
这里增加了一个系数1/2,目的是考虑到对平方项求导后运算方便。这个 Loss 函数称为平方和损失函数。
平方和损失函数,不仅计算方便,而且有非常好的几何意义。看下图,
它们之间的欧式距离为:
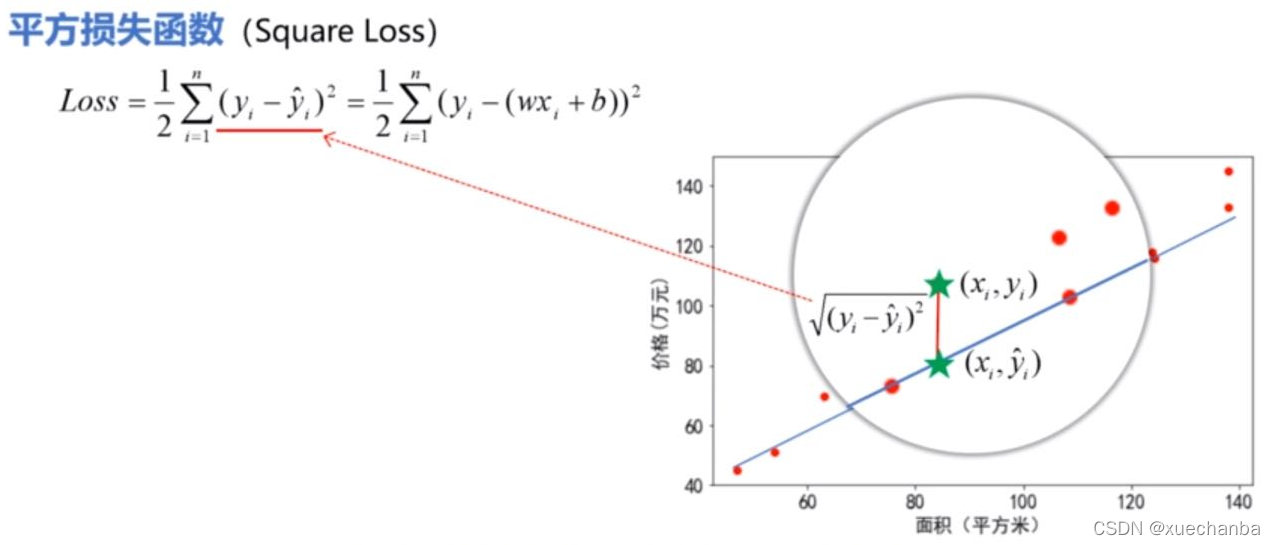
平方损失函数中的每一项其实都反映的是每个样本点和它的估计值之间的欧式距离的大小。因此,所找到的这条直线也就是总体上最接近这些点的直线。
损失函数的性质
除了平方和损失函数,针对不同的问题,还有其他一些损失函数,那么什么样的函数才能够作为损失函数呢?
非负性:它的每一个误差项应为非负的,从而保证样本误差不会相互抵消。
一致性:损失函数的值和误差变化趋势是一致的。即:当模型输出的估计值与样本标签y差距越大时,损失函数的值就应该越大,而当它们越接近时,函数的值就应该越小,并且不断地趋于0,也就是说应该单调有界,并且收敛于0。
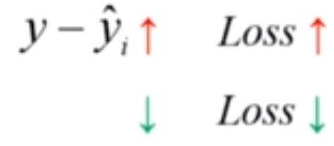
对平方损失函数再除以样本数n,就是均方误差。在实际的编程应用中,我们经常使用到它作为衡量误差的指标。基于均方误差最小化,来进行的模型求解的方法,称为最小二乘法。

最小二乘法的应用并不仅仅局限于线性回归,在线性回归中,最小二乘法就是试图找到一条直线,使所有样本到直线上的欧式距离之和最小。
求解过程
在模型求解阶段,所有的样本数据都是已知的,模型参数w和b是变量。不同的取值对应不同的直线,现在需要确定w和b取值为多少时,可以使得损失函数的取值达到最小。显然,这是一个求解最小值问题,我们知道求解极值点的偏导数必然为0。因此,只要分别对 w 和 b 求偏导数就可以了。
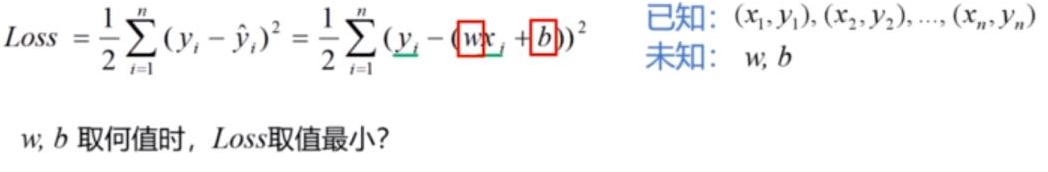

下图分别是对w和b求偏导数,
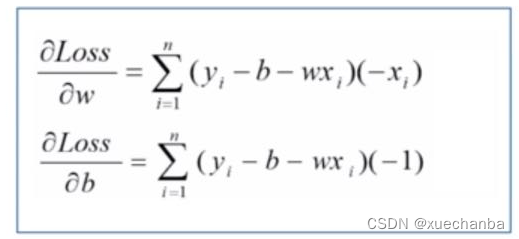
让他们的结果等于0。
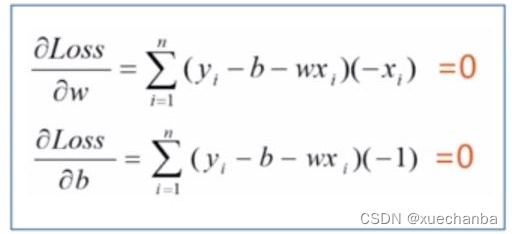
求解这个方程组,就可以得到w和b的值,求得到的值就是使得损失函数达到最小值的模型参数。求解这个方程组并不困难。
求解的过程不同,得到的求解结果也自然不同,例如,下面两个结果。
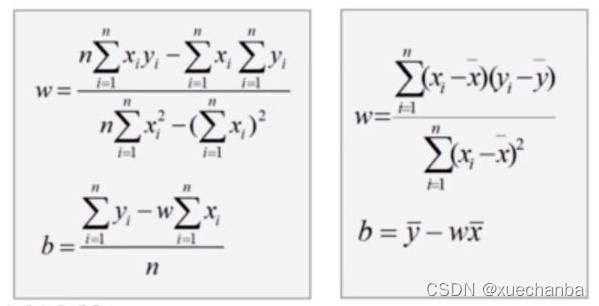
左图为视频授课老师计算的结果,两个结果虽然形式上不同,但是两个结果是等价的,可以通过等式变换得到。显然,右图这种形式看起来更加的简洁。在后面的实例中,也会采用右图的这种解来编写程序。
对于这种求解的过程是根据严格的公式推导和计算得到的,这样得到的解也被称之为解析解。解析解是一个封闭形式的函数,即给出任意的自变量,就可以通过严格的公式求出准确的因变量。因此,解析解也被称之为封闭解或者闭式解。
