对于逻辑回归算法主要是用回归的算法解决分类的问题,它只能解决二分类的问题,经过改造便可以进行多分类问题,主要的改造方式有两大类:
(1)OVR/A(One VS Rest/ALL)
(2)OVO(One VS One)
(1)对于OVR的改造方式,主要是指将多个分类结果(假设为n)分成是其中一种分类结果的和(其他),这样便可以有n种分类的模型进行训练,最终选择得分最高的的(预测率最高的的)便为分类结果即可。它所训练的时间是原来分类时间的n倍。sklearn库默认就是OVR
(2)对于OVO的方式,主要是将n个数据分类结果任意两个进行组合,然后对其单独进行训练和预测,最终在所有的预测种类中比较其赢数最高的即为分类结果,这样的分类方式最终将训练分为n(n-1)/2个模型,计算时间相对较长,不过这样的方式每次训练各个种类之间不混淆也不影响,因此比较准确。
有一个疑问:n是如何确定的?
from sklearn.linear_model import LogisticRegression
classifier = LogisticRegression(random_state=0) #建立逻辑回归模型
其中LogisticRegressiom()底层代码:
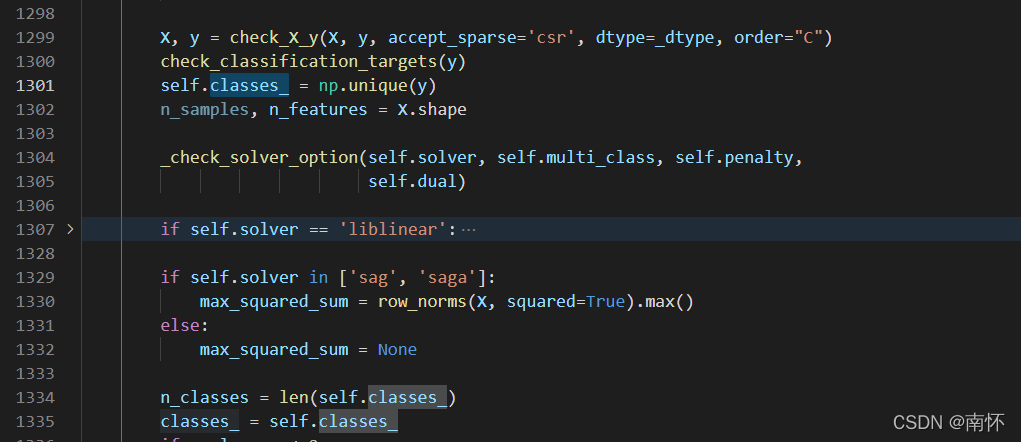
1301行和1334行就是求出n值,即类别的个数,np.unique()作用是将y去重并按元素大小返回一个新的无元素重复的元组或列表。
self.classes_ = np.unique(y) #1301行
n_classes = len(self.classes_)#1334行
自己简单实现,以鸢尾花数据集为例,是一个根据花的属性给花进行分类的数据集,共有3类150条记录,每类各50个数据。
import numpy as np #导入numpy库,简写为np
import matplotlib.pyplot as plt #导入matplotlib库,简写为plt
from sklearn.datasets import load_iris
y = load_iris().target
print(type(y)) #y有150个
classes_ = np.unique(y)
print(classes_) #一个新的无元素重复的元组 [0 1 2 ]
n_classes = len(classes_)
print(n_classes) #类别的个数 3
结果如下:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
[0 1 2]
3
引用:
https://zhuanlan.zhihu.com/p/453182477
