原文链接:
Batch Normalization究竟学到了数据的什么信息?
大家好,我是泰哥。上节为大家介绍了数据归一化的发展历程,本节就讲讲Batch Normalization的计算思路,看看它究竟强在哪里?为什么它可以使模型梯度保持平稳。
1 归一化不会改变数据分布
任何归一化的本质都是对数据进行平移和放缩。
- 平移:数据集每一列数据统一加上或减去某一个数
- 缩放:数据集每一列数据统一除以或乘以某一个数
import torch
import matplotlib.pyplot as plt
# 生成200个黄色数据集,标签为1
yellow = torch.normal(mean = 2, std = 2, size=(200, 2))
yellow_label = torch.ones(size = (yellow.shape[0], 1))
# 生成200个紫色数据集,标签为0
purple = torch.normal(mean = 8, std = 2, size=(200, 2))
purple_label = torch.zeros(size = (purple.shape[0], 1))
# 合并数据集
data = torch.cat((yellow, purple), dim = 0)
label = torch.cat((yellow_label, purple_label), dim = 0)
# 查看其分布
plt.scatter(data[:, 0], data[:, 1], c = label)
而数据的平移和放缩,不会影响数据特征的分布情况。

接下来,我们使用Z-score对其进行归一化操作,然后对比查看归一化前后数据集分布:
def z_score(t):
std = t.std(0)
mean = t.mean(0)
ans = (t - mean) / std
return ans
zs_data = z_score(data)
# 然后对比查看归一化前后数据集分布
plt.figure(figsize=(12, 6))
plt.subplot(121)
plt.scatter(data[:, 0], data[:, 1], c = label)
plt.title('data distribution')
plt.subplot(122)
plt.scatter(zs_data[:, 0], zs_data[:, 1], c = label)
plt.title('zs_data distribution')
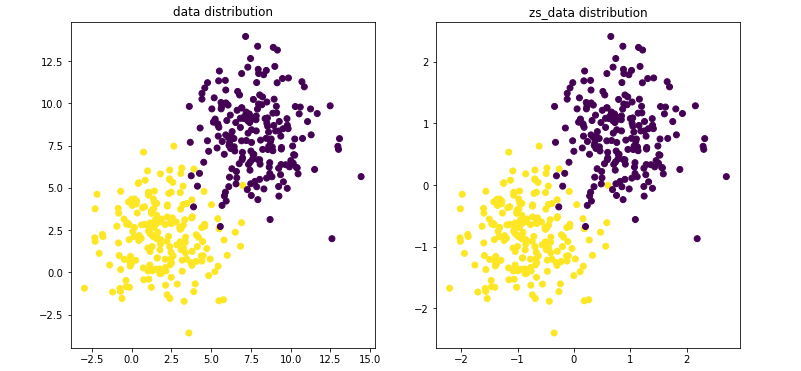
可以发现,数据在坐标中的绝对值会发生变化,但是归一化前后数据分布不变。
2 归一化其实是仿射变化
数据的仿射变换用矩阵形式来进行表示就是: x ^ = x ? w + b \hat x = x * w + b x^=x?w+b其中x是原数据,w是参数矩阵,b是截距, x ^ \hat x x^是经过变换之后的数据。此处以Z-Score为例,探讨归一化操作转化为仿射变换的方法。
在归一化运算时,我们进行了如下操作:
x
?
m
e
a
n
(
x
)
s
t
d
(
x
)
\frac{x-mean(x)}{std(x)}
std(x)x?mean(x)?
稍作变换,就可以写成如下表达式:
x
s
t
d
(
x
)
?
m
e
a
n
(
x
)
s
t
d
(
x
)
=
x
?
1
s
t
d
(
x
)
?
m
e
a
n
(
x
)
s
t
d
(
x
)
\begin{aligned} \frac{x}{std(x)} - \frac{mean(x)}{std(x)} \\ = x \cdot\frac{1}{std(x)}- \frac{mean(x)}{std(x)} \\ \end{aligned}
std(x)x??std(x)mean(x)?=x?std(x)1??std(x)mean(x)??
与
x
^
=
x
?
w
+
b
\hat x = x * w + b
x^=x?w+b形式相同了,但在BN中会写作
x
?
γ
+
β
x \otimes \gamma + \beta
x?γ+β,其中
?
\otimes
?表示逐个元素相乘,
γ
和
β
\gamma 和\beta
γ和β为指代参数。
3 将平移与缩放设为参数
那么在归一化的过程中,放缩的部分可以通过矩阵乘法来完成,而平移部分则更加简单,让数据集加上由每一列平移幅度所构成的向量即可完成。
在实际操作中,我们将归一化操作看成一个特殊的线性层,也将极大拓展归一化操作可以出现的位置。在经典机器学习领域,对数据的归一化只停留在输入数据时对数据进行统一处理,那么在迭代过程中,数据会逐渐失去初始化之后所带来的良好特性,此时如果我们可以像添加线性层一样,在任意隐藏层前后添加归一化层进行处理,就能避免迭代过程中数据逐渐偏移所导致的梯度不平稳问题。
g
r
a
d
3
=
?
l
o
s
s
?
y
^
?
F
(
F
(
X
?
w
1
)
?
w
2
)
grad_3 = \frac{\partial loss}{\partial \hat y} \cdot F(F(X * w_1) * w_2)
grad3?=?y^??loss??F(F(X?w1?)?w2?)
实际上均值为0、方差为1的归一化不一定是最优选择,根据各层梯度计算公式不难看出,最佳的数据归一化方法并不是绝对的0均值1方差,而是能够使得最终各变量(输入、参数、激活函数)相乘之后梯度保持均衡。
4 BN实际流程
BN的平移和放缩分为两个阶段:
- 第一个阶段是先将数据进行Z-Score处理
- 第二阶段则是在此基础上在对数据的均值进行参数平移,并对其方差进行参数放缩
其实两个阶段做的是一件事,就是对参数进行平移和缩放。我们可以将第一阶段理解为将数据本身的均值与方差设为了初始值,第二阶段则是根据反向传播来不断的更新参数。
最终训练结束,数据将朝向方差为 γ \gamma γ、均值为 β \beta β的分布方向靠拢。
5 BN的衍生
在BN诞生之后,根据不同的业务场景,又衍生出了原理相同的一些方法,比如Layer Normalization、instance normalization、Group Nomalization。
它们只是选择了数据的不同维度进行了缩放与平移,但是与BN的原理一致。
