introduction
本文提出了一种基于区域的全卷积神经网络用于目标检测,取得了与Faster R-CNN差不多的精度,但在训练和推理方面表现更好。FCN有两个亮点:
- 不同于Fafster RCNN ,执行上百次代价高昂的RoI,FCN全卷积几乎共享在整张图像上的计算
- 提出了位置敏感score maps用于解决图像分类的平移不变性与目标检测任务的平移同变性之间的矛盾。(因为网络既要用于分类又要用于检测)
池化层,也具有局部平移不变性,例如3X3的最大池化,在给定的3X3感受野范围内,无论像素位置如何移动,最后输出的都是最大的那个值,一旦超出这个范围,就不再具有不变性,GAP(全局平局池化)就拥有全局平移不变性,因为它是在整个特征映射上做平均池化。
与不变性对应的叫作平移可变(同变)性(translation -variance),目标检测任务中就需要平移可变性,一个物体在图像中的位置发生了移动,那么对用的边界框坐标也要跟着变化。随着卷积网络加深,平移不变性会增强,平移可变性会变差,这就导致了分类和检测的矛盾。
根据论文,当前流行的目标检测网络(Fater R-CNN 、Fast RCNN)基于之对应网络可以分为两种: 1. 独立于RoIs 的全卷积网络,共享计算 2. 不共享计算的RoI子网络 这是由之前的卷积网络AlexNet等结构延续下来的,一个卷积结构(末尾使用空间池化)+几个全连接层,因此图像分类任务中的空间池化层自然而然的被转换成目标检测任务中的RoI 池化层。
Network
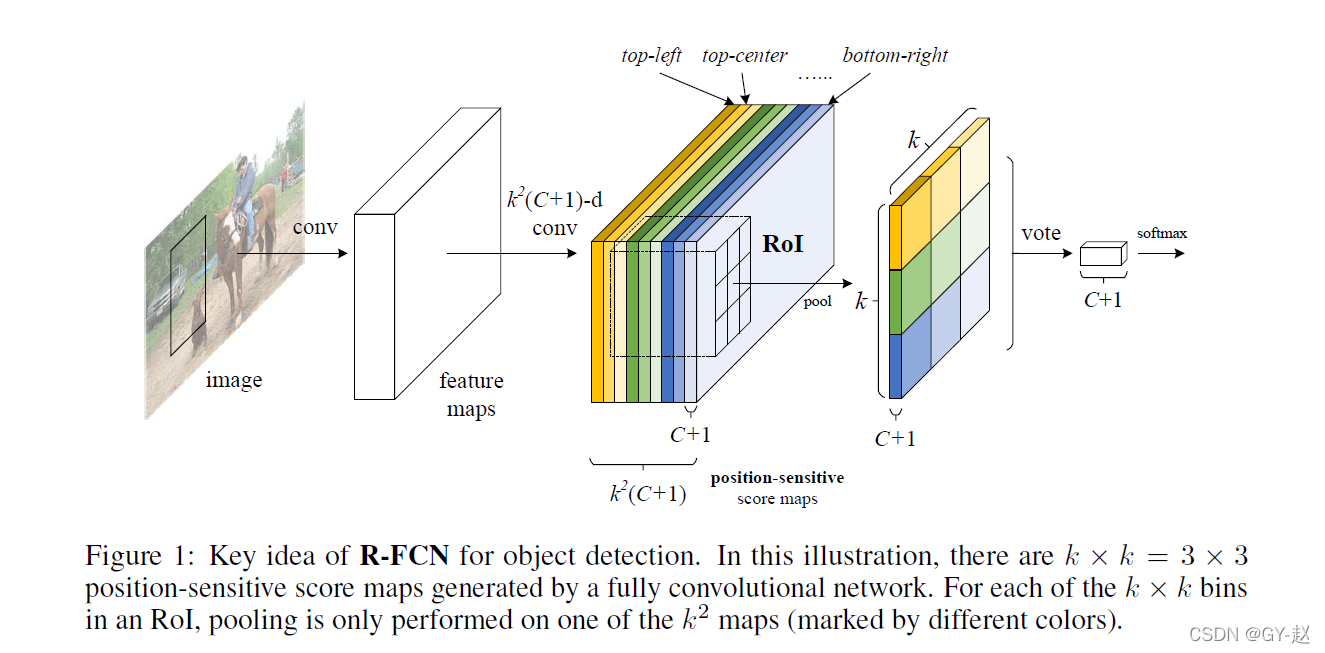
FCN由共享的、全卷积的架构组成,为了将平移同变性引入FCN,作者使用一组专门的卷积层构造了一组位置敏感的分数图作为FCN的输出。每一个分数图都是用相对空间位置进行位置信息编码。上图中不同颜色分数图对应不同的空间位置。在FCN之后,附加一个位置敏感的RoI池化层从这些分数图中获取信息(之后没有权重层【卷积或全连接】)。整个结构都是端到端学习的,所有可学习的层都是卷积层,在整个图像上计算共享。由于对目标检测的空间信息进行了编码,R-FCN作为一个全卷积神经网络,仍然具有平移同变性。
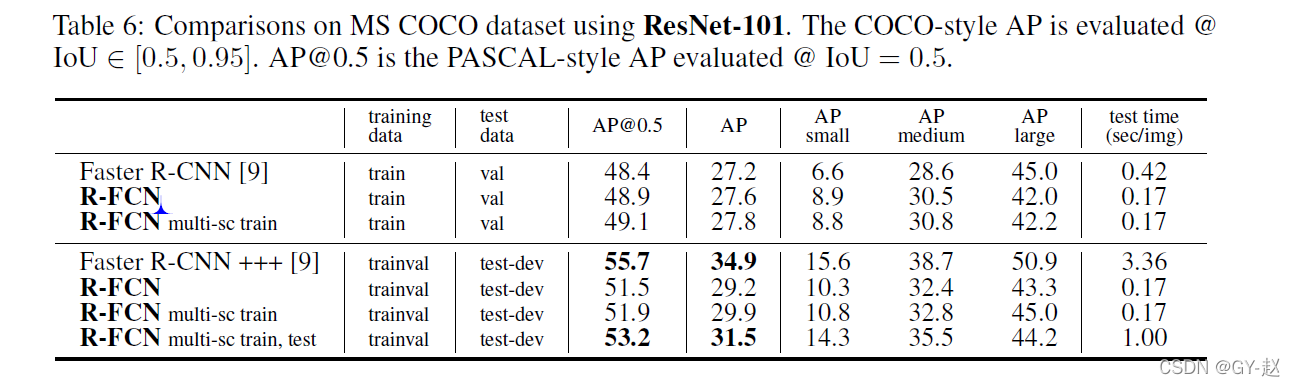
使用101层的ResNet作为backbone,R-FCN在PASCAL VOC2007上取得了83.6%mAP,同时检测速度达到170ms/一张图像,比起同样使用ResNet101的Faster R-CNN 速度要快2.5–20倍。
Overview Architecture
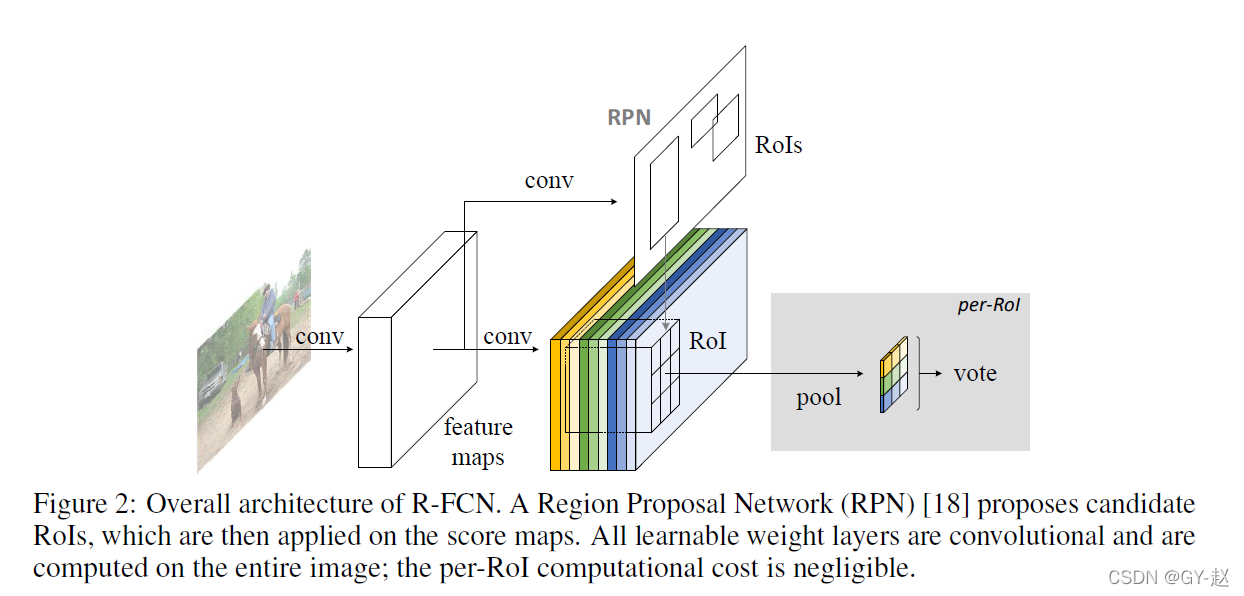
遵循类似RCNN的两阶结构:
- region proposal
- region classification
通过RPN区域建议网络来提取候选框,该网络本事是一个全卷积网络,之后在RPN与R-FCN之间共享了特征。上图展示了系统总体框架。
在给定建议区域RoIs的情况下,R-FCN结构被设计将RoIs分为目标类别和背景。在R-FCN中,所有的可学习参数都是卷积且在整张图像进行计算。最后一个卷积层为每一个类别输出 K 2 K^2 K2个位置敏感的分数图,因此有一个 K 2 ( C + 1 ) K^2(C+1) K2(C+1)个通道的输出层(C:目标类别数目+ 1:背景)。 K 2 K^2 K2个分数图对应于描述位置的 K ? K K*K K?K个空间网格。例如, K ? K = 3 ? 3 K*K=3*3 K?K=3?3,9个分数图编码了一个对象类别的{top-left, top-center, top-right, …, bottom-right}等位置。例如person类,person边界框的中上位置总是与人的头部相对应,因此对于原始输入图像与person类别对应的特征图训练,尽可能是使得特征图中中上位置与person对应的点的得分高一点。
R-FCN以一个位置敏感的RoI池化层作为末端。这一层聚集了最后一个卷积层而输出,并为每个RoI生成生成分数。在图2中9个特征图,这些特征图上每个特征点上的值对应该点所属位置的得分。
位置敏感score map && 位置敏感 RoI 池化
为了显示的将位置信息编码到每一个RoI,把每一个RoI分割成
K
?
K
K*K
K?K个矩形格子。对于一个尺寸为
w
?
h
w*h
w?h的长方形RoI来说,一个格子的尺寸为
w
k
?
h
k
\frac{w}{k}*\frac{h}{k}
kw??kh?.最后一个卷积层为每一个类别生成
K
2
K^2
K2个分数图,在第
(
i
,
j
)
(i,j)
(i,j)个格子
(
0
≤
i
,
j
≤
k
?
1
)
(0\le i,j\le k-1 )
(0≤i,j≤k?1),定义一个位置敏感的池化层只在第
(
i
,
j
)
(i,j)
(i,j)个分数图上进行平均池化操作:
r
c
(
i
,
j
∣
Θ
)
=
∑
(
x
,
y
)
∈
b
i
n
(
i
,
j
)
z
i
,
j
,
c
(
x
+
x
0
,
y
+
y
0
∣
Θ
)
/
n
?
?
?
?
(
1
)
r_c(i,j|\Theta )=\sum_{(x,y)\in bin(i,j)}z_{i,j,c}(x+x_0,y+y_0|\Theta )/n ---- (1)
rc?(i,j∣Θ)=(x,y)∈bin(i,j)∑?zi,j,c?(x+x0?,y+y0?∣Θ)/n????(1)
这里
r
c
(
i
,
j
)
r_c(i,j)
rc?(i,j)指在第C个类别的第
(
i
,
j
)
(i,j)
(i,j)格子的池化响应,
z
i
,
j
,
c
z_{i,j,c}
zi,j,c?是
K
2
(
C
+
1
)
K^2(C+1)
K2(C+1)个score map中的一个score map 输出。
(
x
0
,
y
0
)
(x_0,y_0)
(x0?,y0?)代表RoI的左上角(top-left),遍历RoI的起点,n是格子(bin)中的像素个数,用来求平均。
Θ
\Theta
Θ表示网络中所有的可学习参数。第
(
i
,
j
)
(i,j)
(i,j)个格子保持
[
i
w
k
]
≤
x
<
[
(
i
+
1
)
w
k
]
a
n
d
[
j
h
k
]
≤
y
<
[
(
j
+
1
)
h
k
]
[i\frac{w}{k}]\le x <[(i+1)\frac{w}{k} ]and [j\frac{h}{k} ]\le y <[(j+1)\frac{h}{k}]
[ikw?]≤x<[(i+1)kw?]and[jkh?]≤y<[(j+1)kh?]. 具体操作如图1所示。一种颜色表示一对
(
i
,
j
)
(i,j)
(i,j),公式1执行了平均池化,但是最大池化结果也不错。
接着这 K 2 K^2 K2个位置敏感的分数对RoI进行投票(Vote)。本文中简单的通过平均分数来进行投票,为每一个RoI产生一个 ( C + 1 ) (C+1) (C+1)维的向量: r c ( Θ ) = ∑ ( i , j ) r c ( i , j ∣ Θ ) r_c(\Theta)=\sum_{(i,j)}r_c(i,j|\Theta) rc?(Θ)=∑(i,j)?rc?(i,j∣Θ)
然后计算跨类别softmax: s c ( Θ ) = e r c ( Θ ) / ∑ c ′ = 0 C e r c ′ ( Θ ) s_c(\Theta)=e^{r_{c}(\Theta)}/\sum_{c^{\prime }=0}^{C}e^{r_{c^{\prime}}(\Theta)} sc?(Θ)=erc?(Θ)/∑c′=0C?erc′?(Θ) 用于评估训练过程中的交叉熵损失,并用于在推理过程中对RoI进行排序。
作者使用类似的方法解决了bounding box回归。除了之前的 K 2 ( C + 1 ) K^2(C+1) K2(C+1)维的卷积层之外,增加了一个 4 K 2 4K^2 4K2维的卷积层用于bounding box回归,在这个 4 K 2 4K^2 4K2的maps上执行位置敏感的RoI池化,为每一个RoI生成一个 4 k 2 4k^2 4k2的向量。然后通过平均VOTE汇聚成一个4-d向量。这个4-d向量参数化一个bounding box 为 t = ( t x , t y , t w , t h ) t=(t_x,t_y,t_w,t_h) t=(tx?,ty?,tw?,th?)表示建议框的坐标。为了简单起见,执行与类无关的边界框回归,但特定类的边界框回归也是可行的。
在RoI池化层之后没有需要学习的层,它引导目标检测的分数图的学习,从而实现了几乎零成本的区域计算,加快了训练和推理。

可视化正确/不正确位置敏感分数图,位置敏感的分数图作为位置敏感的RoI池化层的输入,在RoI pooling中,对RoI中不同位置区域对应的分数图上进行池化操作,例如在RoI左上区域在位置敏感的分数图中表示对左上区域进行池化。该层最后输出 K ? K ? ( C + 1 ) K*K*(C+1) K?K?(C+1)的位置敏感的聚合RoI。
在聚合的RoI上进行投票是一个简单的平均值计算过程,即对C+1个KxK区域的值求平均,得到一个C+1维的向量,使用softmax函数计算最终类别。
损失函数
位置敏感的RoI损失函数包括分类交叉熵损失与边界框回归损失两部分:
L
(
s
,
t
x
,
t
y
,
t
w
,
t
h
)
=
L
c
l
s
(
s
c
?
)
+
λ
[
c
?
>
0
]
L
r
e
g
(
t
,
t
?
)
L(s,t_x,t_y,t_w,t_h)=L_{cls}(s_{c*})+\lambda [c^{*}>0]L_{reg}(t,t^{*})
L(s,tx?,ty?,tw?,th?)=Lcls?(sc??)+λ[c?>0]Lreg?(t,t?)
其中,
c
?
c^*
c?是RoI的真实类别标签,
c
?
=
0
c^*=0
c?=0表示背景。若RoI为背景,则边界框回归损失的系数将变为0.
L
c
l
s
(
s
c
?
)
=
?
l
o
g
(
s
c
?
)
L_{cls}(s_{c*})=-log(s_{c*})
Lcls?(sc??)=?log(sc??)表示分类交叉熵损失,
s
c
?
s_{c*}
sc??表示以anchor i为目标得预测概率。
L
r
e
g
L_{reg}
Lreg?和Fast R-CNN中的边界框回归损失一样,是一个smooth L1损失。
R-FCN训练过程中也使用了难负样本挖掘方法,同样使用4步训练法交替训练RPN与R-FCN。
实验结果