[人工智能]从零实现深度学习框架——N-Gram语言模型(二)

引言

本着“凡我不能创造的，我就不能理解”的思想，本系列文章会基于纯Python以及NumPy从零创建自己的深度学习框架，该框架类似PyTorch能实现自动求导。

要深入理解深度学习，从零开始创建的经验非常重要，从自己可以理解的角度出发，尽量不使用外部完备的框架前提下，实现我们想要的模型。本系列文章的宗旨就是通过这样的过程，让大家切实掌握深度学习底层实现，而不是仅做一个调包侠。

本文接上一篇，主要介绍解决零概率问题的平滑方法。

N的选择

N-gram模型依赖于训练语料。随着$N$的增加，N-gram的表现越来越好。但是$N$太大会导致计算量非常大，以及零概率项过多的问题。一般取$N=3$或$N=4$。

零概率

上面说的零概率一种可能是有些组合同时出现的频数为0。比如有些零概率项由于在训练集中从未出现过，而只在测试集中出现。那么在测试的时候，就会给它赋予零概率。它们的存在意味着我们低估了可能出现的各种单词的概率。

未登陆词

上面我们说的零概率是由于只在测试集中出现的组合。那如果碰到从未见过的单词怎么办？

这里简单介绍两种词汇系统，一种是开放词汇系统，另一种是封闭词汇系统。在封闭词汇系统中，所有的单词都是预先知道的，测试集只包含这些单词，不会有未知的单词。而开放词汇系统，则可能会包含从未见过的单词，一般添加一个伪单词<UNK>来表示这些词。

这种没见过的单词，称为未登陆词(out of vocabulary,OOV)。

有两种方法解决这个问题，一是转换为封闭词汇，通过提前设定一个固定大小的词典：

1. 选择固定大小的词典
2. 将不在训练集中的任何单词转换为未登录词标记<UNK>
3. 从<UNK>的计数中估计它的概率，就像对训练集中其他单词一样

第二种方法是在我们没有预先词典的情况下，隐式地创建这样一个单词，根据频率用<UNK>替换训练数据中的单词。例如我们可以用<UNK>取代所训练集中出现次数少于n次的单词，其中n是一些小数值，或提前选择一个词汇量V（比如50000），然后选择保留top V的单词并替换剩余的单词为<UNK>。在任何一种情况下，我们都会像以前一样训练语言模型，将<UNK>当作一个常规单词。

平滑

平滑技术为了解决我们上面说的零概率项问题。不管你的训练语料库有多大，总会有一些从未见过的词。比如只在测试集中从未见过的上下文出现。为了防止语言模型为这些未见过的项分配零概率，我们需要对之前的概率分配进行一定调整，提高零概率，降低高概率。不患寡而患不均，类似劫富济贫的思想。

这种调整被称为平滑。平滑技术主要有三种：

• 折扣法(Discounting)：从已观察概率中分配一些给未观察到的概率
• 插值法(Interpolation)：将高阶模型和低阶模型进行混合
• 回退法(Back-off)：利用低阶模型来近似估计未观察到的高阶模型

下面一一介绍。

拉普拉斯平滑

拉普拉斯平滑(Laplace smoothing)又称为加1平滑(Add-1 smoothing)，该方法在归一化概率前，将所有的N-gram计算加$1$。从而避免出现零概率问题。

我们知道归于单词$w_i$的未平滑Unigram概率的最大似然估计算为，它出现的计数$c_i$，除以单词总数$N$:
$$P(w_i)=\frac{c_i}{N}\text{\hspace{1em}(16)}$$

单词总数$N$说的是语料库中的所有单词的总数，包含重复计数；而词典中共有$V$个单词说的是去重之后，语料库由这$V$个单词组成的。

拉普拉斯平滑为每个分子都加$1$。因为词典中共有$V$个单词，每个增加$1$，因此我们也需要调整分母：
$$P_{Laplace}(w_i)=\frac{c_i+1}{N+V}\text{\hspace{1em}(17)}$$
由于上述平滑算法同时概率概率计算中的分子和分母，这样对照分析该平滑方法前后的计数时不方便，因此我们可以定义一个修正后的计数$c^{?}$，这样在保持分母相同的情况下，观察计数的变化情况。引入归一化参数$\frac{N}{N+V}$，经过拉普拉斯平滑修正后的unigram计数$c_i^{?}$为：
$$c_i^{?}=(c_i+1)\frac{N}{N+V}\text{\hspace{1em}(18)}$$
我们只要除以$N$就可以将$c_i^{?}$转换为概率$P_i^{?}$。

查看平滑的一种方法是降低(折扣)一些非零计数，然后分配给零计数。我们可以用相对折扣$d_c$来描述一种平滑算法，即折扣计数与原始计数的比率：
$$d_c=\frac{c^{?}}{c}\text{\hspace{1em}(19)}$$
下面我们看一下拉普拉斯平滑给概率值带来的影响，例子来自于Speech and language processing。

有一个餐厅对话训练语料，假设下面这些单词的unigram计数为：

然后给出训练语料中一小部分bigram计数，其中大部分bigram计数都为0，从左到右看，比如i want出现的次数为$827$，i chinese出现的次数为$0$。

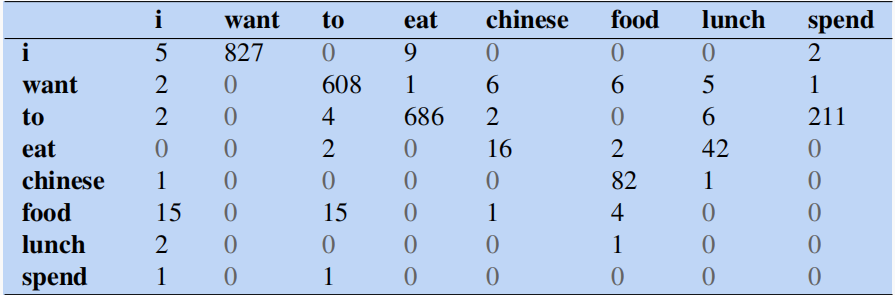
在未加入平滑之前，我们可以结合unigram和bigram计数计算出归一化的bigram概率为：

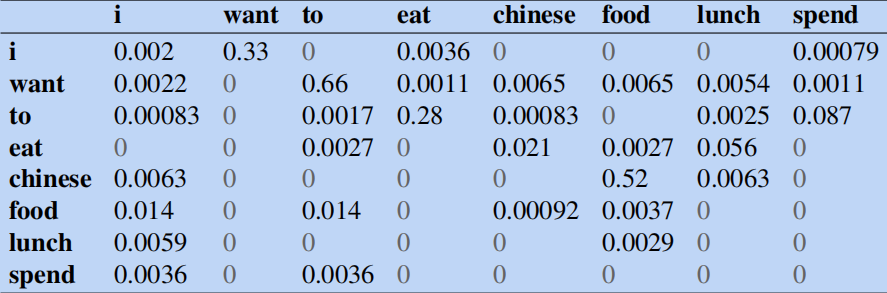
比如(根据公式$(9)$)计算$p(want|i)$：
$$p(want|i)=\frac{C(iwant)}{C(i)}=\frac{827}{2533}\approx 0.33$$
下面我们进行拉普拉斯平滑，更新bigram的计数表：

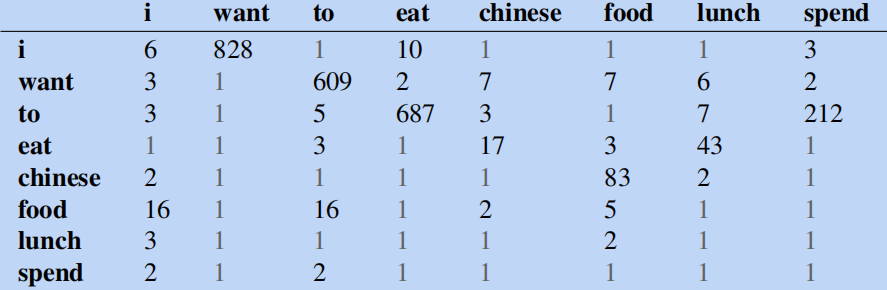
然后基于词汇表中$V=1446$计算拉普拉斯概率：
$$P_{\text{Laplace}}(w_n|w_{n?1})=\frac{C(w_{n?1}{w}_n)+1}{{\sum }_w(C(w_{n?1}w)+1)}=\frac{C(w_{n?1}{w}_n)+1}{C(w_{n?1})+V}\text{\hspace{1em}(20)}$$
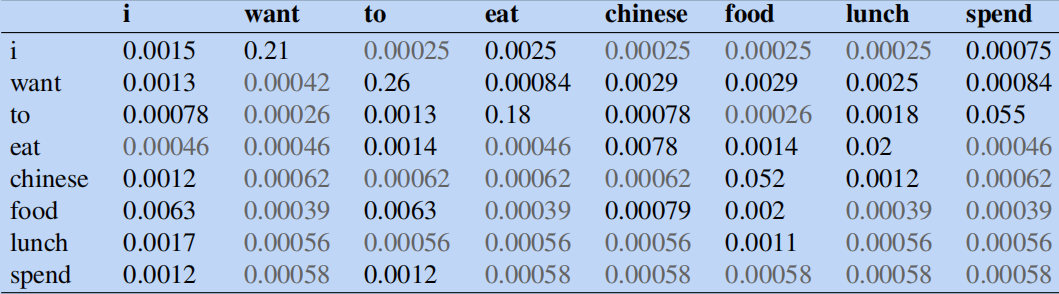
得到平滑的bigram概率：

为了方便地查看平滑算法对原始计数修改了多少，通常可以重构计数表。可以通过下面的公式计算修正后次数：
$$c^{?}(w_{n?1}{w}_n)=\frac{[C(w_{n?1}{w}_n)+1]\times C(w_{n?1})}{C(w_{n?1})+V}\text{\hspace{1em}(21)}$$
根据上式得修正后的计数表如下：

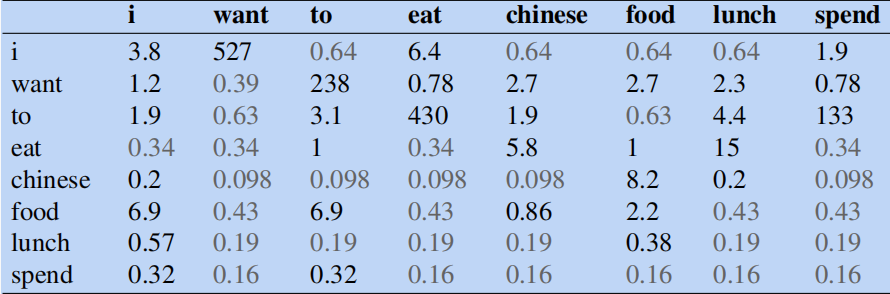
可以看到拉普拉斯平滑对原始计数进行了较大修改。比如$C(wantto)$从$609$减少为$238$。也可以从概率空间中看到这一点：$p(to|want)$从$0.66$下降到了$0.26$。

由于该概率值带来的修改过大，我们可以考虑更加温柔的版本——加K平滑。

加K平滑

加K平滑(Add-k smoothing)将加1平滑中增加的计数值由$1$改成一个小于$1$的数$k$(0.5/0.05/0.01)。
$$P_{\text{Add-k}}^{?}(w_n|w_{n?1})=\frac{C(w_{n?1}{w}_n)+k}{C(w_{n?1})+kV}\text{\hspace{1em}(22)}$$
Add-k平滑要求我们有选择k的方法；例如，这可以通过优化开发集来实现。虽然add-k对某些任务（包括文本分类）很有用，但事实证明，它在语言建模应用中效果较差。

我们现在了解的都是折扣法，下面我们来看下回退和插值法。

回退和插值

假设我们想计算$P(w_n|w_{n?2}{w}_{n?1})$，但是没有$w_{n?2}{w}_{n?1}{w}_n$这种trigram样本，那么我们降低要求，使用bigram概率$P(w_n|w_{n?1})$来估计$P(w_n|w_{n?2}{w}_{n?1})$，这种方法就叫回退。类似地，如果我们也有$w_{n?1}{w}_n$，那么可以直接用unigram概率$P(w_n)$。

在回退中，如果数据充足，我们使用trigram，否则我们使用bigram，甚至使用unigram。即我们没有高阶n-gram的数据时，我们才会回退到低阶n-gram。而插值中，总是混合所有阶的n-gram估计的概率，并进行加权。

在简单的线性插值中，我们通过线性插值来组合不同阶的n-gram。因此，我们通过将unigram、bigram和trigram概率混合在一起来估计trigram概率$P(w_n|w_{n?2}{w}_{n?1})$，每个概率都以一个$\lambda$权重加权：
$$\begin{array}{rl}\hat{P}(w_n|w_{n?2}{w}_{n?1})& ={\lambda }_{1}P(w_n)\\ & +{\lambda }_{2}P(w_n|w_{n?1})\\ & +{\lambda }_{3}P(w_n|w_{n?2}{w}_{n?1})\end{array}\text{\hspace{1em}(23)}$$
这些权重$\lambda$的和为$1$，使公式$(23)$等同于一个加权平均：
$$\sum _i{\lambda }_i=1\text{\hspace{1em}(24)}$$

在稍微复杂的线性插值版本中，每个$\lambda$权重都是以上下文为条件计算的：
$$\begin{array}{rl}\hat{P}(w_n|w_{n?2}{w}_{n?1})& ={\lambda }_1(w_{n?2:n?1})P(w_n)\\ & +{\lambda }_2(w_{n?2:n?1})P(w_n|w_{n?1})\\ & +{\lambda }_3(w_{n?2:n?1})P(w_n|w_{n?2}{w}_{n?1})\end{array}\text{\hspace{1em}(25)}$$
这些$\lambda$值是如何设置的？简单的插值和条件插值的$\lambda$都是从保留语料库中学习的。保留语料库(类似验证集)是一种额外的训练语料库，之所以这么叫它，是因为我们从训练数据中分离它，我们用它来设置像这些$\lambda$值这样的超参数。

我们通过选择$\lambda$值来最大化保留语料库的似然来做到这一点。也就是说，我们固定n-gram概率，然后搜索插值等式$(23)$时的$\lambda$值——使得保留集出现最高概率。有多种方法可以找到这套最佳$\lambda$，比如使用EM算法。

为了让回退模型给出正确的概率分布，我们必须折扣高阶n-gram，为低阶n-gram保留一些概率密度，正如拉普拉斯平滑一。如果高阶n-gram没有折扣，而我们只是使用未折扣的MLE概率，那么一旦我们将有零概率的n-gram替换为低阶n-gram，那么语言模型分配给所有可能字符串的总概率将大于1！除了这个显式折扣系数外，我们还需要一个函数$\alpha$来将这个概率密度分配到低阶n-gram。

这种折扣的回退也被称为Katz回退。在Katz回退中，如果我们以前见过这个n-gram（即如果我们有非零计数），那么我们依赖折扣概率$P^{?}$。否则，我们为更短的历史(N-1)-gram递归回退到Katz概率。回退n-gram的概率$P_{BO}$计算如下：
$$P_{BO}(w_n|w_{n?N+1:n?1})=\{\begin{array}{ll}{P}^{?}(w_n|w_{n?N+1:n?1})& \text{if?C(wn?N+1:n?>0)}\\ \alpha (w_{n?N+1:n?1})P_{BO}(w_n|w_{n?N+2:n?1})& \text{otherwise}\end{array}\text{\hspace{1em}(26)}$$
Katz回退通常与一种名为Good-Turing的平滑方法相结合。

我们重点来看一下Kneser-Ney平滑。

Kneser-Ney平滑

Kneser-Ney平滑方法是一种扩展的绝对折扣方法，采用了一种更精细的方法处理低阶unigram分布。

绝对折扣的意思是让每个计数减去固定(绝对)值$d$。

为了看到这一点，我们可以使用Church和Gale提出的一个聪明的想法。考虑一个计数为4的n-gram。我们需要给每个计算减去某个数值，那么减去多少呢？

Church和Gale想法是看一个保留(held out)的语料库，看看在训练集中计数为$4$的bi-gram计数在保留语料库中是什么。他们从AP newswire的2200万个单词中计算出一个bi-gram语法，然后在另外2200万个单词的保留语料库中检查了这些bi-gram的计数。平均而言，在前2200万个单词中出现4次，在接下来的2200万个单词中出现3.23次。如下图显示了$c$从0到9的bi-gram的计数。

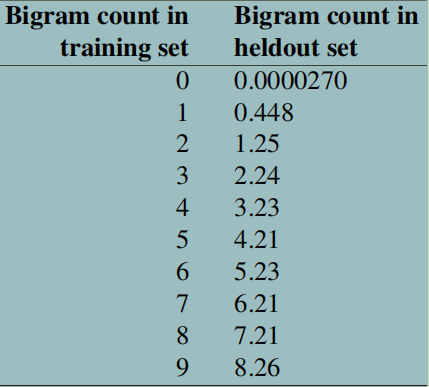
从上面的统计可以看到，除了$c=0$或$c=1$，其他所有的在保留集中的bigram计数几乎都比训练集中少$0.75$。

而绝对折扣将这种直接公式化，通过让每个计数减去固定(绝对)值$d$。对于非常大的计数，减去这么一个小的折扣值不会影响什么。对于低频词更看重unigram的插值。如果将绝对折扣应用到bigram上得到的公式如下：
$$P_{\text{AbsoluteDiscounting}}(w_i|w_{i?1})=\frac{C(w_{i?1}{w}_i)?d}{{\sum }_{v}C(w_{i?1}v)}+\lambda (w_{i?1})P(w_i)\text{\hspace{1em}(27)}$$
其中第一项是折扣bigram，第二项是带插值权重的unigram。我们可以简单的将$d$设成$0.75$。

上面说的是绝对折扣，那么Kneser-Ney平滑在此基础上做了什么呢？

考虑下面这样一个预测下一个单词的例子，假设我们插值一个bigram和unigram模型。

I can’t see without my reading __

假设现在有替补词汇glasses和Kong。根据语境这里更应该是单词glasses，我们得期望我们的unigram模型倾向于glasses。但是实际上Kong这个单词更常见，因为Hong Kong出现的更频繁。标准的unigram模型会为Kong赋予更高的概率。

因此Kneser-Ney的思想是：低阶模型的概率不应该与其频数成正比，而应该与其能组成的不同词组的种类数成正比。因为假设某个单词能形成的不同词组越丰富，那么该单词越容易与其他单词组成新的词组，因此概率应该越高。

这里定义一个unigram模型称为$P_{CONTINUATION}$，表示单词$w$作为新的延续词的可能性。那么我们如何估计单词$w$在未知上下文中作为新延续词的概率呢？Kneser-Ney的做法是基于单词$w$过去在不同上下文中出现的次数，即由它完成的bigram类型数量。如果某个单词过去在更多的不同上下文中出现，那么我们认为它也更可能在新的上下文中出现。单词$w$在新的延续中出现的次数可以表示为：
P CONTINUATION ( w ) ∝ ∣ { v : C ( v w ) > 0 } ∣ (28) P_{\text{CONTINUATION}} (w) ∝ |\{v:C(vw) > 0\}| \tag{28} PCONTINUATION?(w)∝∣{v:C(vw)>0}∣(28)
这里$v$是前面的单词，$vw$表示前面是$v$，接着是$w$的情况，$C(vw)$表示这两个单词出现过的次数，只会计数第一次出现。这里的$>0$表示我们只会考虑存在的词组。

为了让其变成概率，我们归一化所有的bigram类型数量：
P CONTINUATION ( w ) = ∣ { v : C ( v w ) > 0 } ∣ ∣ { ( u ′ , w ′ ) : C ( u ′ w ′ ) > 0 } ∣ (29) P_{\text{CONTINUATION}}(w) = \frac{ |\{v:C(vw) > 0\}|}{ |\{(u^\prime,w^\prime):C(u^\prime w^\prime) > 0\}|} \tag{29} PCONTINUATION?(w)=∣{(u′,w′):C(u′w′)>0}∣∣{v:C(vw)>0}∣?(29)
类似地，还可以计算先于$w$的不同类型词组数量：
P CONTINUATION ( w ) ∝ ∣ { v : C ( v w ) > 0 } ∣ (30) P_{\text{CONTINUATION}} (w) ∝ |\{v:C(vw) > 0\}| \tag{30} PCONTINUATION?(w)∝∣{v:C(vw)>0}∣(30)
归一化则是用单词$v$先于所有单词的数量：
P CONTINUATION ( w ) = ∣ { v : C ( v w ) > 0 } ∣ ∑ w ′ ∣ { v : C ( v w ′ ) > 0 } ∣ (31) P_{\text{CONTINUATION}}(w) = \frac{ |\{v:C(vw) > 0\}|}{ \sum_{w^\prime}|\{ v:C(v w^\prime) > 0\}|} \tag{31} PCONTINUATION?(w)=∑w′?∣{v:C(vw′)>0}∣∣{v:C(vw)>0}∣?(31)
这样常见(Kong)只出现在一个上下文(Hong)中会有一个低的$P_{\text{CONTINUATION}}$概率。

最终Kneser-Ney平滑对bigram的公式为：
$$P_{\text{KN}}(w_i|w_{i?1})=\frac{\max (C(w_{i?1}{w}_i)?d,0)}{C(w_{i?1})}+\lambda P_{\text{CONTINUATION}}(w_i)\text{\hspace{1em}(32)}$$
这里的$\max$是防止出现负数。

总结

N-gram模型就介绍这么多，后面依次介绍word2vec、神经网络语言模型、RNN语言模型和BERT语言模型。

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖