Yolo v5如何更换激活函数?
文章目录
1.1 激活函数更换方法🍀
(1)找到activations.py,激活函数代码写在了activations.py 文件里.
打开后就可以看到很多种写好的激活函数
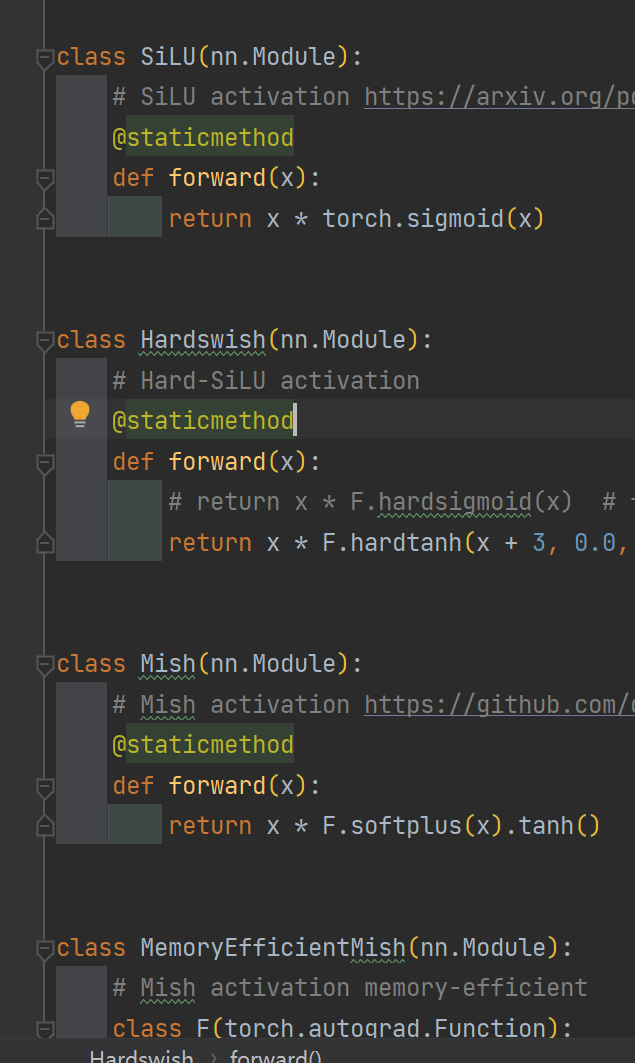
(2)如果要进行修改可以去common.py文件里修改
这里很多卷积组都涉及到了激活函数(似乎就这俩涉及到了),所以改的时候要全面。

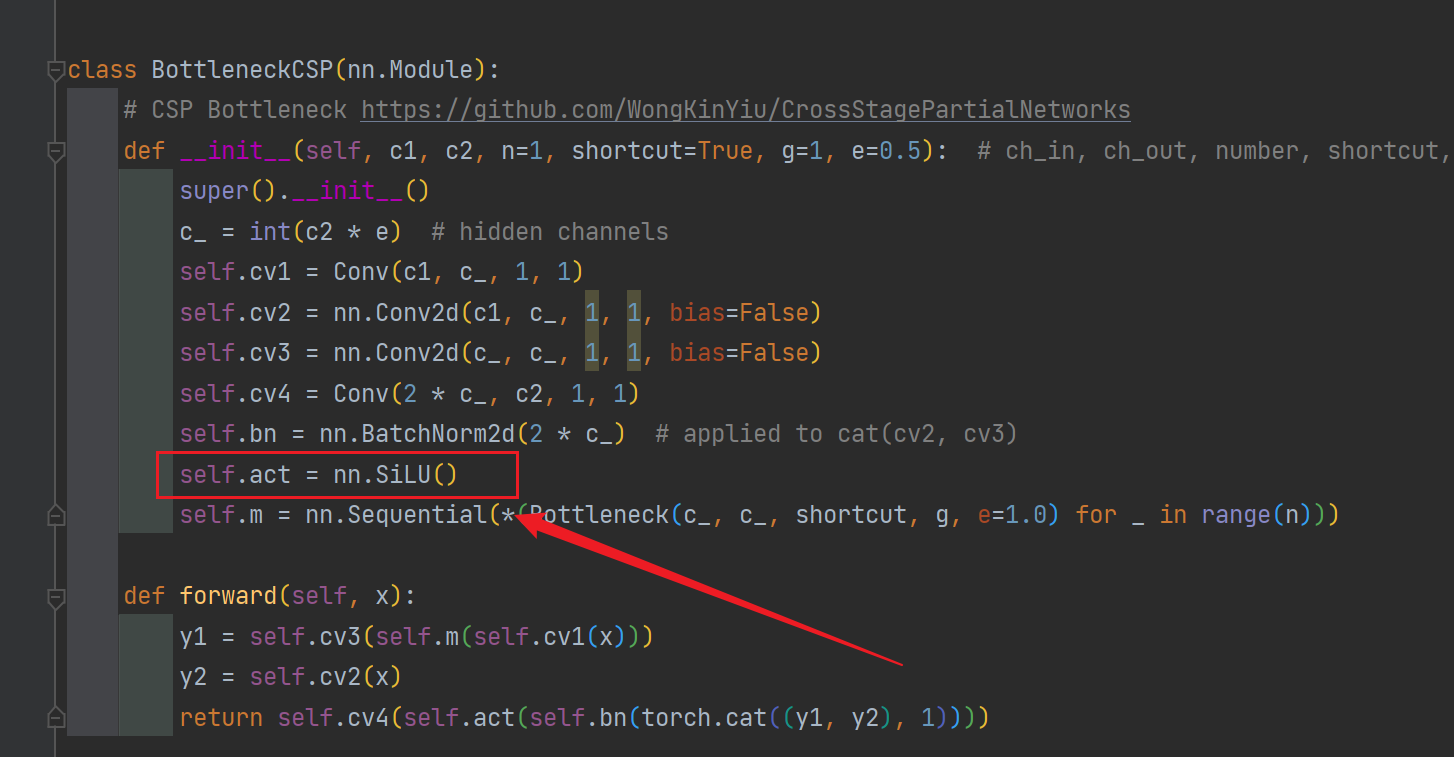
下面放上一些效果比较好的激活函数及图像
1.2 激活函数介绍💡(持续更新中,以后会放上最新paper的复现结果)
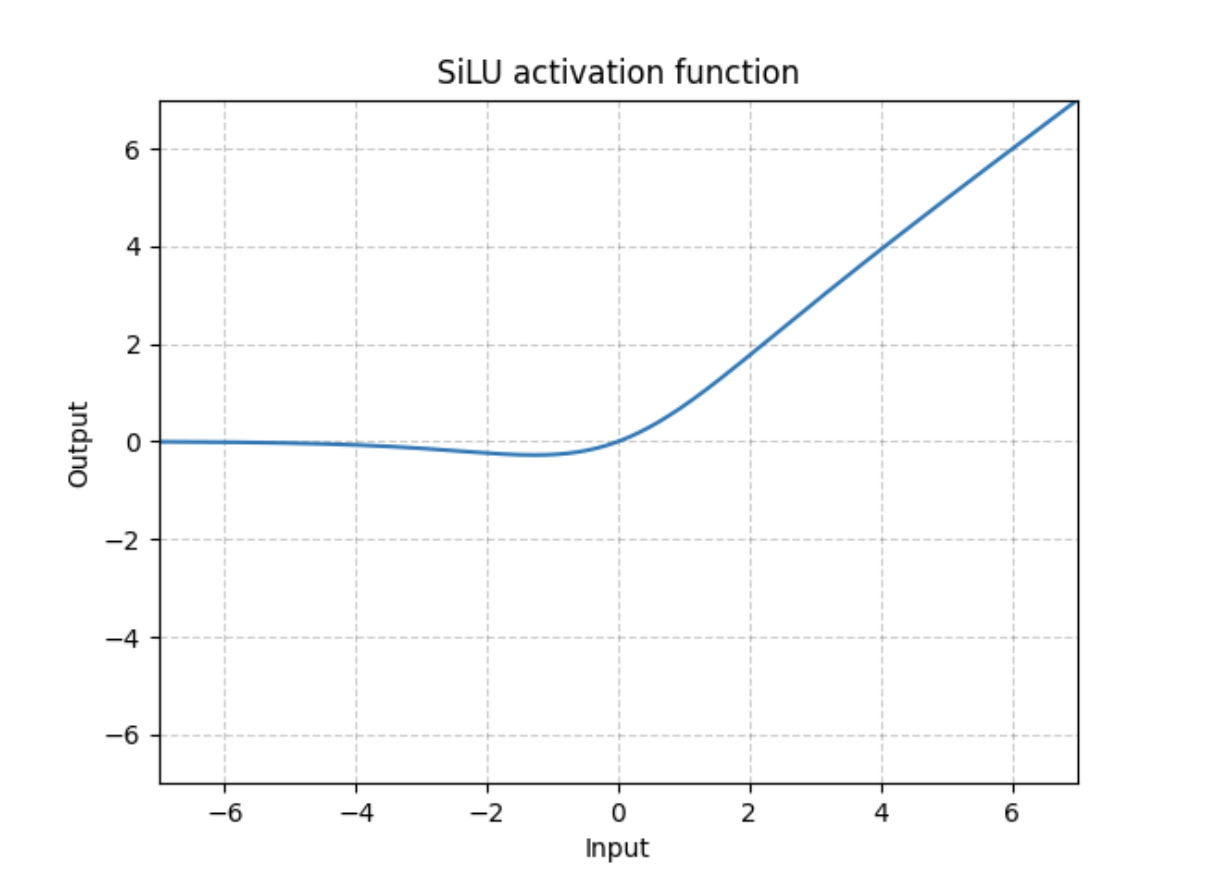
1.2.1 SiLU
SiLU优点:
- 无上界(避免过拟合)
- 有下界(产生更强的正则化效果)
- 平滑(处处可导 更容易训练)
- x<0具有非单调性(对分布有重要意义 这点也是Swish和ReLU的最大区别)
# SiLU https://arxiv.org/pdf/1606.08415.pdf ----------------------------------------------------------------------------
class SiLU(nn.Module): # export-friendly version of nn.SiLU()
@staticmethod
def forward(x):
return x * torch.sigmoid(x)
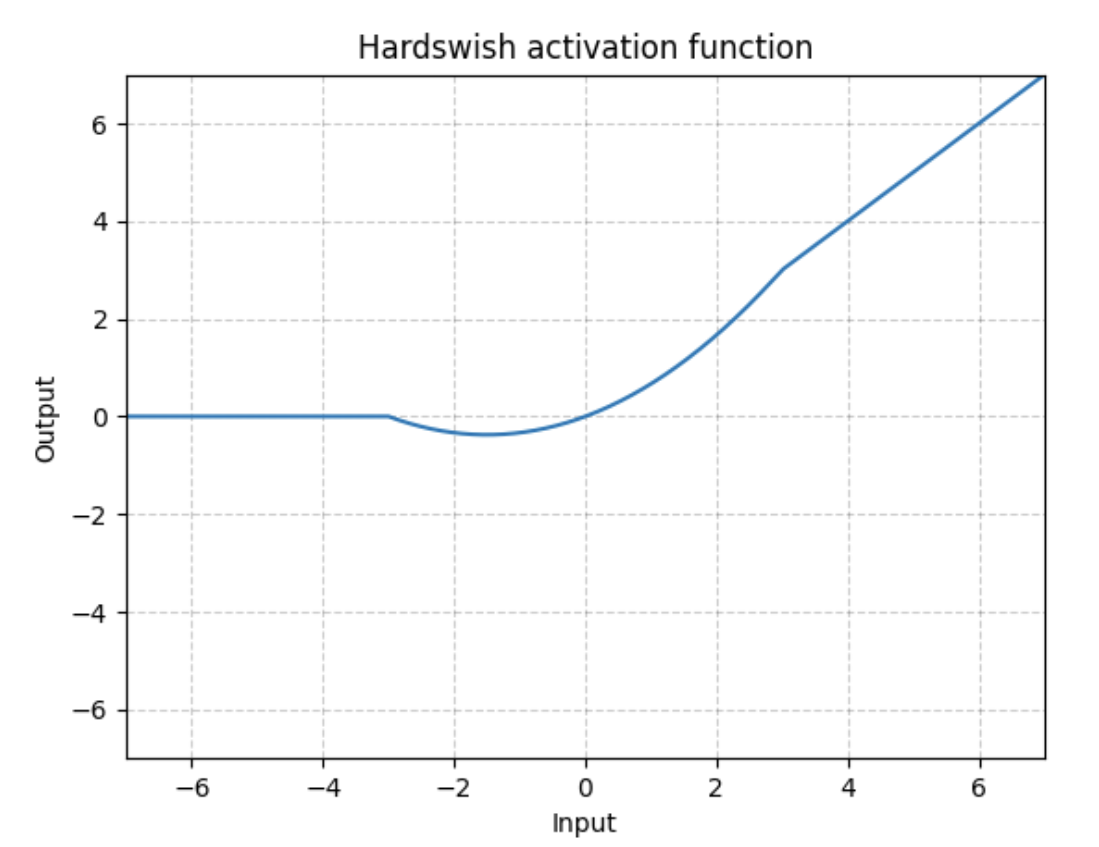
1.2.2 Hardswish
class Hardswish(nn.Module): # export-friendly version of nn.Hardswish()
@staticmethod
def forward(x):
# return x * F.hardsigmoid(x) # for TorchScript and CoreML
return x * F.hardtanh(x + 3, 0.0, 6.0) / 6.0 # for TorchScript, CoreML and ONNX
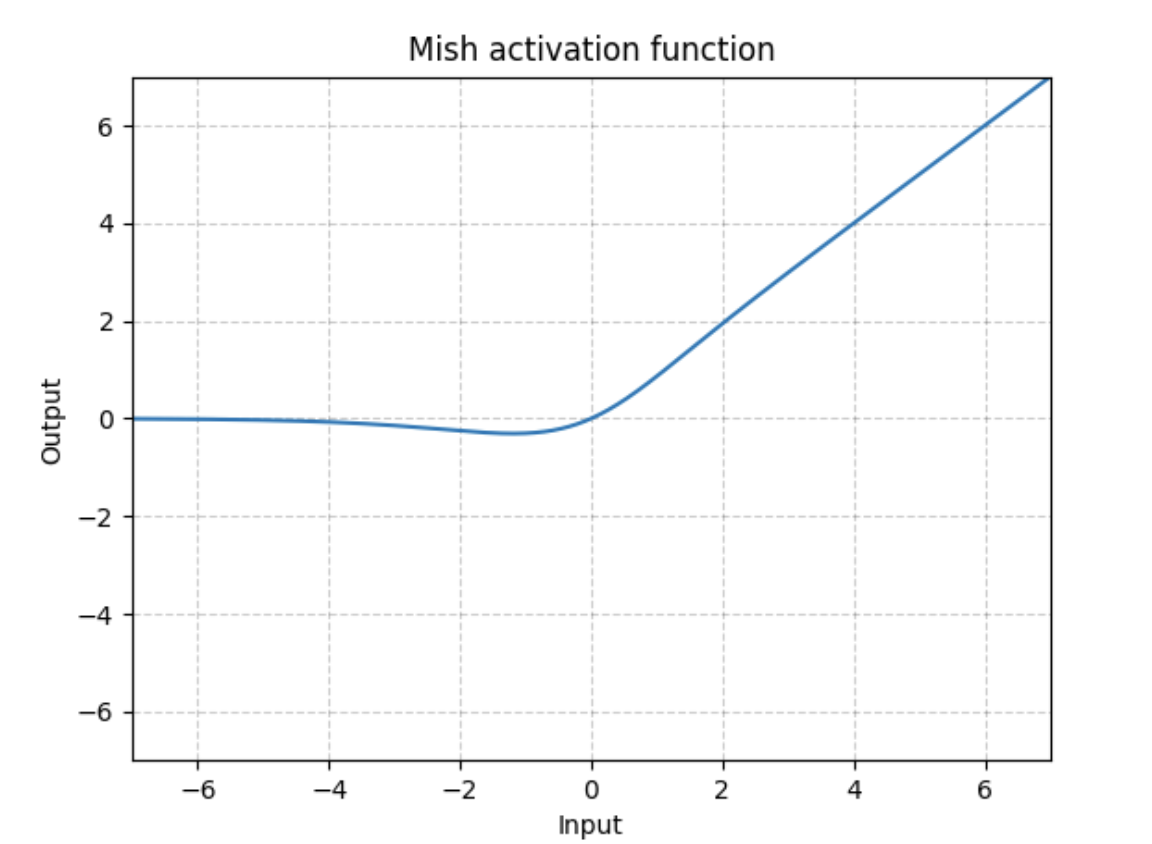
1.2.3 Mish
Mish特点:
1.无上界,非饱和,避免了因饱和而导致梯度为0(梯度消失/梯度爆炸),进而导致训练速度大大下降;
2.有下界,在负半轴有较小的权重,可以防止ReLU函数出现的神经元坏死现象;同时可以产生更强的正则化效果;
3.自身本就具有自正则化效果(公式可以推导),可以使梯度和函数本身更加平滑(Smooth),且是每个点几乎都是平滑的,这就更容易优化而且也可以更好的泛化。随着网络越深,信息可以更深入的流动。
4.x<0,保留了少量的负信息,避免了ReLU的Dying ReLU现象,这有利于更好的表达和信息流动。
5.连续可微,避免奇异点
6.非单调
# Mish https://github.com/digantamisra98/Mish --------------------------------------------------------------------------
class Mish(nn.Module):
@staticmethod
def forward(x):
return x * F.softplus(x).tanh()
1.2.4 MemoryEfficientMish
一种高效的Mish激活函数 不采用自动求导(自己写前向传播和反向传播) 更高效,Mish的升级版
class MemoryEfficientMish(nn.Module):
class F(torch.autograd.Function):
@staticmethod
def forward(ctx, x):
ctx.save_for_backward(x)
return x.mul(torch.tanh(F.softplus(x))) # x * tanh(ln(1 + exp(x)))
@staticmethod
def backward(ctx, grad_output):
x = ctx.saved_tensors[0]
sx = torch.sigmoid(x)
fx = F.softplus(x).tanh()
return grad_output * (fx + x * sx * (1 - fx * fx))
def forward(self, x):
return self.F.apply(x)
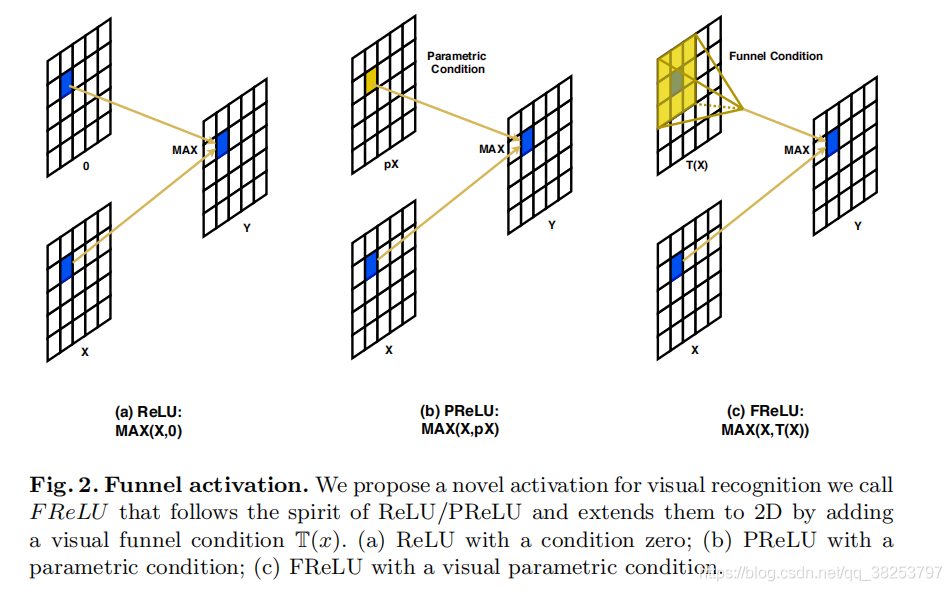
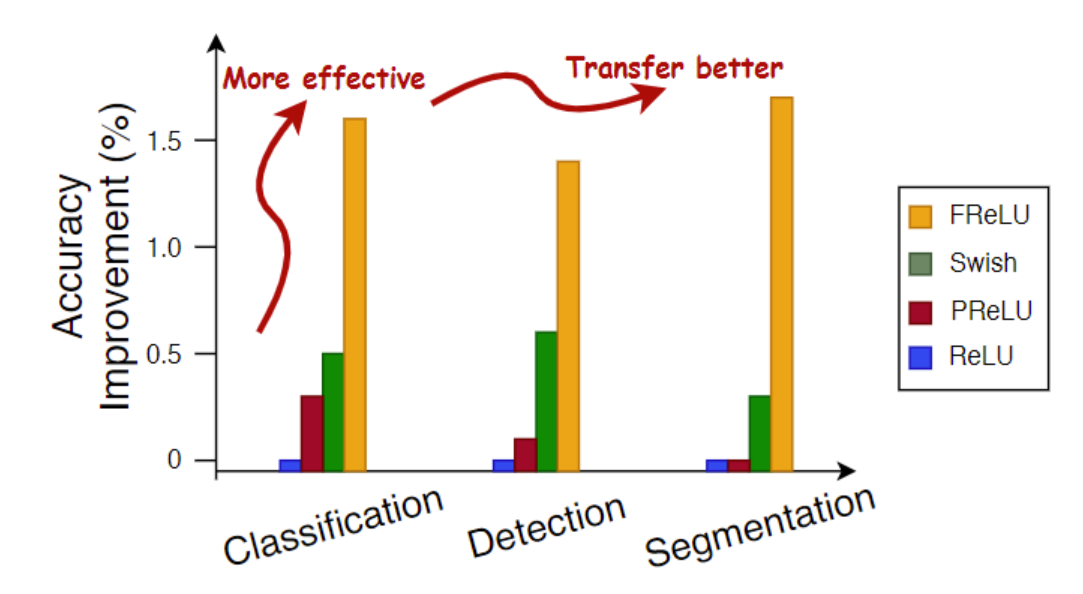
1.2.5 FReLU
FReLU(Funnel ReLU 漏斗ReLU)非线性激活函数,在只增加一点点的计算负担的情况下,将ReLU和PReLU扩展成2D激活函数。具体的做法是将max()函数内的条件部分(原先ReLU的x<0部分)换成了2D的漏斗条件(代码是通过DepthWise Separable Conv + BN 实现的),解决了激活函数中的空间不敏感问题,使规则(普通)的卷积也具备捕获复杂的视觉布局能力,使模型具备像素级建模的能力。
# FReLU https://arxiv.org/abs/2007.11824 -------------------------------------------------------------------------------
class FReLU(nn.Module):
def __init__(self, c1, k=3): # ch_in, kernel
super().__init__()
self.conv = nn.Conv2d(c1, c1, k, 1, 1, groups=c1, bias=False)
self.bn = nn.BatchNorm2d(c1)
def forward(self, x):
return torch.max(x, self.bn(self.conv(x)))
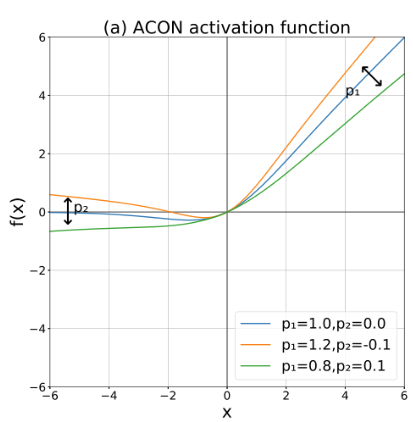
1.2.6 AconC
这是2021年新出的一个激活函数,先从ReLU函数出发,采用Smoth maximum近似平滑公式证明了Swish就是ReLU函数的近似平滑表示,这也算提出一种新颖的Swish函数解释(Swish不再是一个黑盒)。之后进一步分析ReLU的一般形式Maxout系列激活函数,再次利用Smoth maximum将Maxout系列扩展得到简单且有效的ACON系列激活函数:ACON-A、ACON-B、ACON-C。最终提出meta-ACON,动态的学习(自适应)激活函数的线性/非线性,显著提高了表现。
细节请看这位大佬的文章
class AconC(nn.Module):
r""" ACON activation (activate or not).
AconC: (p1*x-p2*x) * sigmoid(beta*(p1*x-p2*x)) + p2*x, beta is a learnable parameter
according to "Activate or Not: Learning Customized Activation" <https://arxiv.org/pdf/2009.04759.pdf>.
"""
def __init__(self, c1):
super().__init__()
self.p1 = nn.Parameter(torch.randn(1, c1, 1, 1))
self.p2 = nn.Parameter(torch.randn(1, c1, 1, 1))
self.beta = nn.Parameter(torch.ones(1, c1, 1, 1))
def forward(self, x):
dpx = (self.p1 - self.p2) * x
return dpx * torch.sigmoid(self.beta * dpx) + self.p2 * x
1.2.7 MetaAconC
上面那个的不同版本
class MetaAconC(nn.Module):
r""" ACON activation (activate or not).
MetaAconC: (p1*x-p2*x) * sigmoid(beta*(p1*x-p2*x)) + p2*x, beta is generated by a small network
according to "Activate or Not: Learning Customized Activation" <https://arxiv.org/pdf/2009.04759.pdf>.
"""
def __init__(self, c1, k=1, s=1, r=16): # ch_in, kernel, stride, r
super().__init__()
c2 = max(r, c1 // r)
self.p1 = nn.Parameter(torch.randn(1, c1, 1, 1))
self.p2 = nn.Parameter(torch.randn(1, c1, 1, 1))
self.fc1 = nn.Conv2d(c1, c2, k, s, bias=True)
self.fc2 = nn.Conv2d(c2, c1, k, s, bias=True)
# self.bn1 = nn.BatchNorm2d(c2)
# self.bn2 = nn.BatchNorm2d(c1)
def forward(self, x):
y = x.mean(dim=2, keepdims=True).mean(dim=3, keepdims=True)
# batch-size 1 bug/instabilities https://github.com/ultralytics/yolov5/issues/2891
# beta = torch.sigmoid(self.bn2(self.fc2(self.bn1(self.fc1(y))))) # bug/unstable
beta = torch.sigmoid(self.fc2(self.fc1(y))) # bug patch BN layers removed
dpx = (self.p1 - self.p2) * x
return dpx * torch.sigmoid(beta * dpx) + self.p2 * x
最后再放一张常见激活函数的图
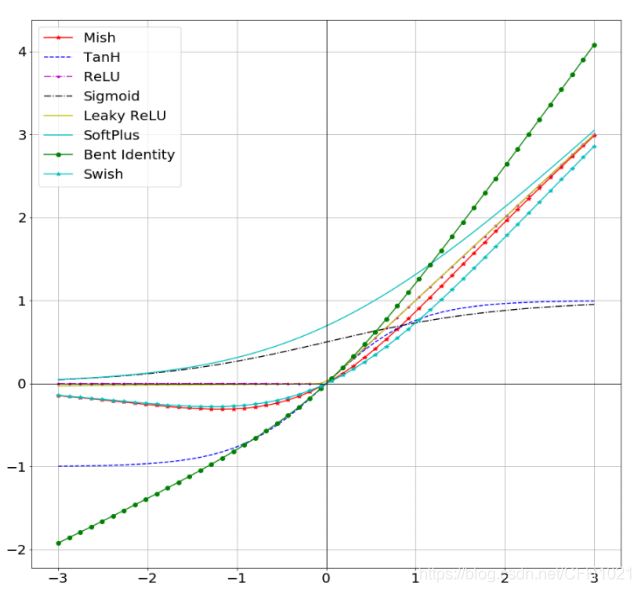
前沿paper的激活函数复现 持续更新中。。。。
