0 前言
此文章主要用于记录IOU、GIOU、DIOU、CIOU存在的缺陷以及各IOU解决的问题。
分析其原理,并附上代码实现。(希望这篇文字能够顺利完成)
1 IOU
1.1 定义
交并比(Intersection over Union)是一种测量在特定数据集中检测相应物体准确度的一个标准。
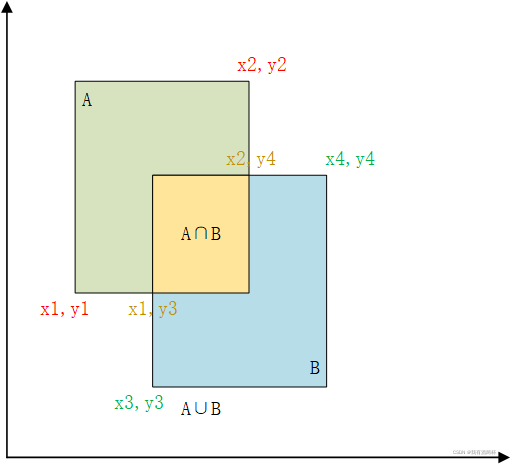
1.2 数学表达式
I
O
U
=
A
∩
B
A
∪
B
IOU=\frac{A\cap B}{A\cup B}
IOU=A∪BA∩B?
A
∩
B
=
(
x
2
?
x
1
)
?
(
y
4
?
y
3
)
A\cap B=\left( x2-x1 \right)*\left( y4-y3 \right)
A∩B=(x2?x1)?(y4?y3)
A
∪
B
=
S
A
+
S
B
?
A
∩
B
=
(
x
2
?
x
1
)
?
(
y
2
?
y
1
)
+
(
x
4
?
x
3
)
?
(
y
4
?
y
3
)
?
(
x
2
?
x
1
)
?
(
y
4
?
y
3
)
A\cup B={{S}_{A}}+{{S}_{B}}-A\cap B=\left( x2-x1 \right)*\left( y2-y1 \right)+\left( x4-x3 \right)*\left( y4-y3 \right)-\left( x2-x1 \right)*\left( y4-y3 \right)
A∪B=SA?+SB??A∩B=(x2?x1)?(y2?y1)+(x4?x3)?(y4?y3)?(x2?x1)?(y4?y3)
IOU的值域范围为0-1,其值越大,表示两个矩形框越接近。
IOU损失
L
i
o
u
=
1
?
I
O
U
{{L}_{iou}}=1-IOU
Liou?=1?IOU
1.3 缺点
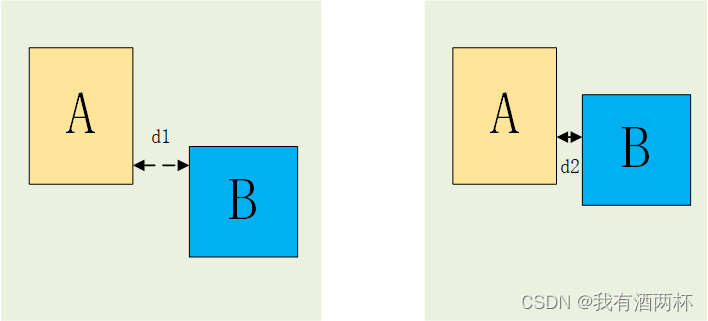
出现下图情况时,IOU将不再有效。
当两个框不存在重叠区域时,右图与左图相比,两个矩形框更接近,其损失应相对较小一些。但此时的IOU值均为0。
1.4 代码
import numpy as np
def calculate_iou(box_gt, box_pd):
'''
计算所有预测框与某个真实框的IOU值
:param box_gt: 真实框 格式[xmin,ymin,xmax,ymax]
:param box_pd: 预测框 格式[[xmin,ymin,xmax,ymax],格式[xmin,ymin,xmax,ymax],格式[xmin,ymin,xmax,ymax] ... ]
:return: IOU
'''
inter_LeftUp = np.maximum(box_pd[:, :2], box_gt[:2]) # 求交集的左上角坐标
inter_RightBot = np.minimum(box_pd[:, 2:4], box_gt[2:4]) # 求交集的右下角坐标
inter_wh = inter_RightBot - inter_LeftUp # 求交集框的宽、高
inter_wh = np.maximum(inter_wh, 0.) # 高和宽小于0的置为0
inter_area = inter_wh[:, 0] * inter_wh[:, 1] # 求交集框的面积 s = w*h
area_gt = (box_gt[2] - box_gt[0]) * (box_gt[3] - box_gt[1]) # 真实框的面积
area_pr = (box_pd[:, 2] - box_pd[:, 0]) * (box_pd[:, 3] - box_pd[:, 1]) # 预测框的面积
iou = inter_area / (area_gt + area_pr - inter_area) # 计算IOU
return iou
2 GIOU
待更新…
