tensorboard所包含的仪表盘主要功能为:
- Scalars?显示损失和指标在每个时期如何变化。 您还可以使用它来跟踪训练速度,学习率和其他标量值。
- Graphs?可帮助您可视化模型。 在这种情况下,将显示层的Keras图,这可以帮助您确保正确构建。
- Distributions?和?Histograms?显示张量随时间的分布。 这对于可视化权重和偏差并验证它们是否以预期的方式变化很有用。
在编写代码时根据这四项的相关要求就可以生成相关的可视化网络。
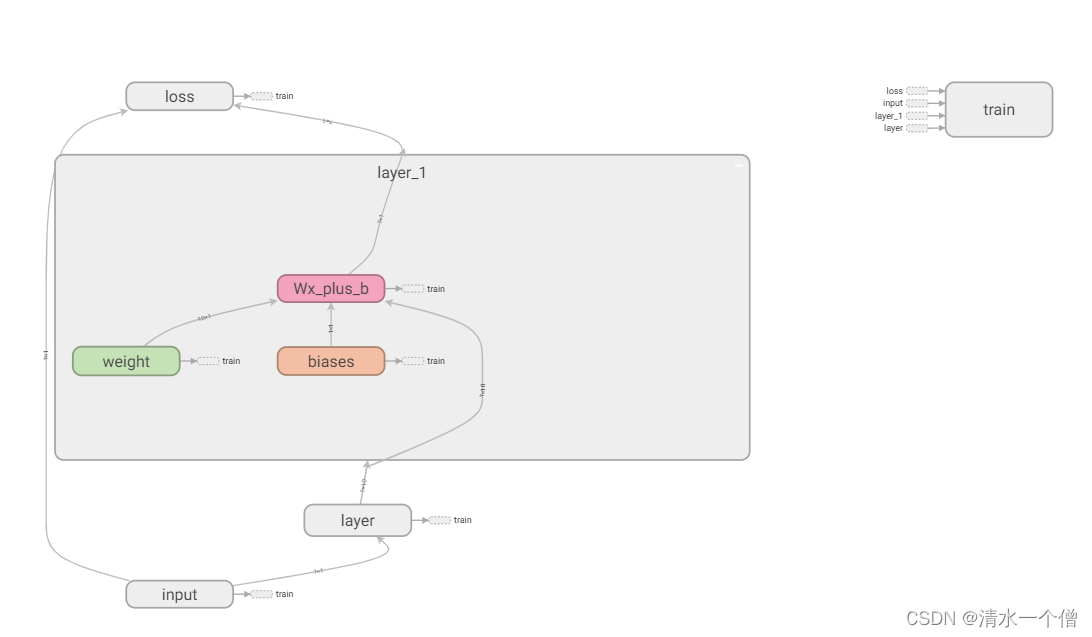
首先如何实现下图这样的效果呢?
下图所展示出来的效果就是在一张图上将神经网络的各个结构画出来,并展示出各个结构之间的连接关系是怎样的。
这里使用tensorflow方法就是with tf.name_scope(),例如我们要在tensorboard中显示一个layer,这一层中包含着权重和偏差,这时代码可以设计为:
with tf.name_scope('layer'):
with tf.name_scope('weights'):
#在此处再定义权重是怎样的
with tf.name_scope('biases'):
#在此处定义偏差这样出来的效果就是在在这个层中有权重和偏差两项。
只看神经网络的结构是不能满足的,我们还想看到在训练过程中权重和偏差随着训练步数的增加是如何改变的,这时我们需要用到tf.summary.histogram()函数记录。
当想要看到loss函数在每个时期的变化需要用到tf.summary.scalar()函数。
通过tf.summary.merge_all()将上面所有设置添加到tensorboard中
通过tf.summary.FileWriter()创建可视化文件
通过writer.add_summary()将每步添加到上述文件中
下面给出一个可视化完整的例子:
import tensorflow.compat.v1 as tf
import numpy as np
def add_layer(
inputs,
in_size,
out_size,
n_layer,
activation_function=None
):
layer_name='layer%s'%n_layer
with tf.name_scope('layer'):
with tf.name_scope('weights'):
Weights=tf.Variable(tf.random_normal([in_size,out_size]),name='W')
tf.summary.histogram(layer_name+'/weights',Weights)
with tf.name_scope('biases'):
biases=tf.Variable(tf.zeros([1,out_size])+0.1,name='b')
tf.summary.histogram(layer_name+'/biases',biases)
with tf.name_scope('Wx_plus_b'):
Wx_plus_b=tf.add(tf.matmul(inputs,Weights),biases)
if activation_function is None:
outputs=Wx_plus_b
else:
outputs=activation_function(Wx_plus_b)
tf.summary.histogram(layer_name+'/outputs',outputs)
return outputs
x_data=np.linspace(-1,1,300,dtype=np.float32)[:,np.newaxis]
noise=np.random.normal(0,0.05,x_data.shape).astype(np.float32)
y_data=np.square(x_data)-0.5+noise
with tf.name_scope('input'):
xs=tf.placeholder(tf.float32,[None,1],name='x_in')
ys=tf.placeholder(tf.float32,[None,1],name='y_in')
l1=add_layer(xs,1,10,n_layer=1,activation_function=tf.nn.relu)
prediction=add_layer(l1,10,1,n_layer=2,activation_function=None)
with tf.name_scope('loss'):
loss=tf.reduce_mean(tf.reduce_sum(tf.square(ys-prediction),reduction_indices=[1]))
tf.summary.scalar('loss',loss)
with tf.name_scope('traain'):
train_step=tf.train.GradientDescentOptimizer(0.1).minimize(loss)
sess=tf.Session()
merged=tf.summary.merge_all()
writer=tf.summary.FileWriter('logs2/',sess.graph)
sess.run(tf.global_variables_initializer())
for i in range(1000):
sess.run(train_step,feed_dict={xs:x_data,ys:y_data})
if i%50==0:
result=sess.run(merged,feed_dict={xs:x_data,ys:y_data})
writer.add_summary(result,i)
不加入可视化的网络构建代码为:
import tensorflow.compat.v1 as tf
import numpy as np
def add_layer(
inputs,
in_size,
out_size,
n_layer,
activation_function=None
):
layer_name='layer%s'%n_layer
Weights=tf.Variable(tf.random_normal([in_size,out_size]),name='W')
biases=tf.Variable(tf.zeros([1,out_size])+0.1,name='b')
Wx_plus_b=tf.add(tf.matmul(inputs,Weights),biases)
if activation_function is None:
outputs=Wx_plus_b
else:
outputs=activation_function(Wx_plus_b)
return outputs
x_data=np.linspace(-1,1,300,dtype=np.float32)[:,np.newaxis]
noise=np.random.normal(0,0.05,x_data.shape).astype(np.float32)
y_data=np.square(x_data)-0.5+noise
with tf.name_scope('input'):
xs=tf.placeholder(tf.float32,[None,1],name='x_in')
ys=tf.placeholder(tf.float32,[None,1],name='y_in')
l1=add_layer(xs,1,10,n_layer=1,activation_function=tf.nn.relu)
prediction=add_layer(l1,10,1,n_layer=2,activation_function=None)
loss=tf.reduce_mean(tf.reduce_sum(tf.square(ys-prediction),reduction_indices=[1]))
train_step=tf.train.GradientDescentOptimizer(0.1).minimize(loss)
sess=tf.Session()
sess.run(tf.global_variables_initializer())
for i in range(1000):
sess.run(train_step,feed_dict={xs:x_data,ys:y_data})
可以对比着就可以看出差距,以及相应函数的使用方法。
