简介
大家好,我最近刚发完论文可以稍稍放松一段时间,之前就发现越来越多的人在学习神经网络的知识,而且有些同学对其也是十分推崇。其实也不奇怪,哈哈,结合当今地时代背景,不管是在什么领域,大家都希望我们身边地东西变得越来越智能,比如手机,电脑等,甚至像像华为公司开发地鸿蒙系统,把日常地电器和手机连接在一起,从而向用户提供更智能地服务。

(给文章加点图,要不然都是文字太难看了,侵权删)
但是如何才能让我们的生活更加智能呢?答案可能是让机器可以向人类一样进行思考,神经网络作为模仿人类大脑神经元的一种算法恰好可以提供这样的服务。本文仅对基本的Bp神经网络进行介绍,主要推导在BP神经网络反向传播的过程中参数如何调整,并且用matlab简单的模拟了一些BP神经网络的训练过程。
PS:简单介绍一下鸿蒙系统,目前手机主流的操作系统有鸿蒙,安卓以及苹果的系统,鸿蒙系统与他们的本质区别在于鸿蒙系统是面向5g的,有种希望实现万物互联的感觉,从5g的角度去看,鸿蒙确实有着跨时代的意义。
BP神经网络
BP神经网络的结构和过程其实很简单,其结构可以大致分为三部分:(1)输入层,输入数据;(2)隐藏层,处理数据;(3)输出层,输出结果。其过程可以分为正向传播过程和反向传播过程,在正向传播过程中,BP神经网络通过隐层神经元对数据进行处理,从而输出相应结果,在反向传播过程中BP神经网络通过对比真实结果与预测结果之间的误差E来不断调整各层神经元的参数值,从而减小误差,达到理想的效果。调整的原则是是误差不断减小,因此应使权值调整量与误差梯度下降成正比。
大家可以看一下下面的误差公式:
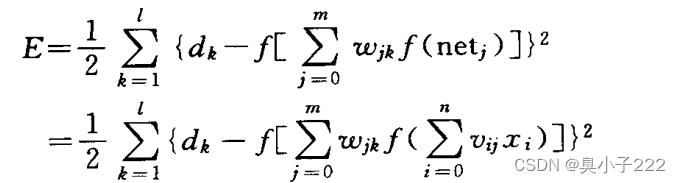
其中E代表误差,d_{k}代表输出层第k个神经元的真实值,后面的f为神经网络的激活函数,此公式代表单隐层的BP神经网络的误差,w_{jk}和v_{ij}为输入层和隐层,以及隐层和输出层之前的权值。
神经网络的权值调整量的求解如下:
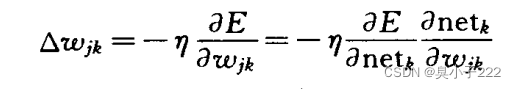
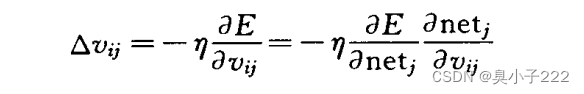
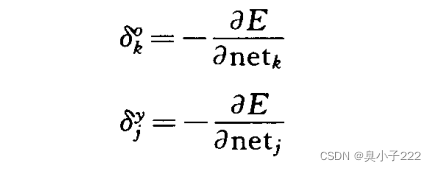
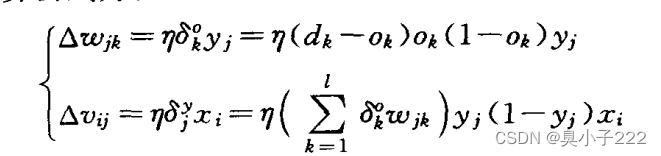
(中间过程实在懒得写了)
不过大家可以看出来,随着隐层的不断增多,需要求的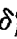
类似这样的参数就越多,如何求出这种参数也是自己实现BP神经网络的关键,参考上面的过程,大家可以看出需要牵扯到符合函数求导的过程,单隐层很简单,单随着隐层数量不断增多,复合函数求导过程也就越复杂,对于多层复合函数需通过链式法则进行求解,但由于过程还是很抽象,大家可以先求解sin(sin2x)这样类推。
BP神经网络流程图
下面的流程图参考当时的教材,BP神经网络其实也分为两种,其区别在于对误差的调整,一种是每输入一个样本就计算相应误差对全职进行调整,也叫标准BP神经网络;二,则是计算所有样本的总误差,也称为屁训练BP神经网络,流程图如下所示:
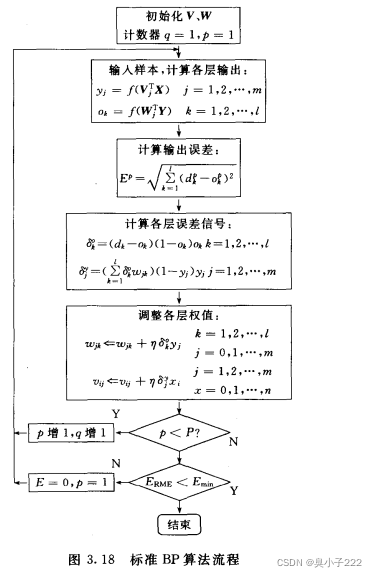
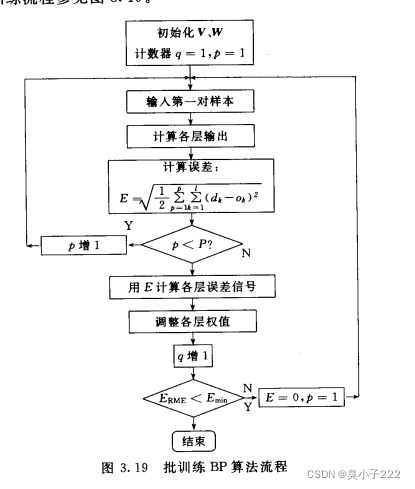
我实现的是标准BP神经网络,代码如下:
input=[1,2,3;4,5,6;7,8,9];
output=[1,2;2,3;3,4];
num=[3,3,3,2];
layer=2;
error=0.1;
iter_time=100;
rate=0.1;
%不通过现有的matlab函数包实现BP神经网络功能
a1=size(input);%输入向量的维度,input的列的维度等于输入节点的个数,input行的维度等于输入数据的数量
a2=size(output);%输出向量的维度,output的列的维度等于输出节点的个数,output行的维度等于输出数据的数量
%初始化权重参数
parameters=cell(1,layer+1);
%layer为隐层的数目
for i=1:layer+1
if i==1
parameters{i}=rand(a1(2),num(i));
elseif i==layer+1
parameters{i}=rand(num(i-1),a2(2));
else
parameters{i}=rand(num(i),num(i));
end
end
%定义神经元的阈值
T=cell(1,layer+2);
for i=1:layer+2
T{i}=ones(1,num(i));%num隐层节点个数
end
i=1;
Error=zeros(1,a1(1));
while i<=iter_time
result=cell(1,layer+1);
%正向传播过程
for j=1:a1(1)
for k=1:layer+1
if k==1
result{k}=ones(1,num(k+1))./[1+exp(input(j,:)*parameters{k}-T{k}*parameters{k})];
else
result{k}=ones(1,num(k+1))./[1+exp(result{k-1}*parameters{k}-T{k}*parameters{k})];
end
end
%计算第j个样本误差
s=0;
for t=1:a2(2)
s=s+(output(j,t)-result{layer}(t));
end
Error(j)=s^(0.5);
%反向传播过程
delta=cell(1,layer+1);%计算反向传播过程中可能需要的参数
for t=1:a2(2)
delta{layer+1}(t)=(output(j,t)-result{layer+1}(t))*result{layer+1}(t)*(1-result{layer+1}(t));
end
for t=layer:-1:1
middle=ones(1,num(t));
for r=1:num(t)
for l=1:num(t+2)
middle(1,r)=middle(1,r)+delta{t+1}(l)*parameters{t}(r,l);
end
delta{t}(r)=middle(r)*result{t}(r)*(1-result{t}(r));
end
end
%调节参数
for t=1:layer+1
for r=1:num(t)
for l=1:num(t+1)
parameters{t}(r,l)=parameters{t}(r,l)+rate*delta{t}(l)*result{t}(l);
end
end
end
%检查误差是否符合要求
E_MSE=(sum(Error.^(2))/a1(1))^(0.5);
if E_MSE<error
break;
end
end
R=result{layer+1};
i=i+1;
end
这个并不能代表完整的BP神经网络算法过程,仅仅是实现了他模拟调整参数的过程,完整的过程还需要对神经网络进行训练,记录其训练好的参数,这样当有了新的输入才能给出准确的输出。
结语
BP神经网络的实现非常简单,但是利用人家·做好的函数可能并不能真正的理解他的原理和过程,虽然这只是重复他人的工作,但我觉得可以加深自己对神经网络的理解。就这样,哈哈哈 有错误或者其他问题欢迎交流。
