三 【案例】SVHN街道实景门牌识别
SVHN全称Street View House Number数据集,它是深度学习诞生初期被创造出来的众多数字识别数据集中的一个,也是唯一一个基于实拍图片制作而成的数字识别数据集。其风格与MNIST数据集相似,每张图像中是裁剪后获得的一个数字,并且是数字0~9相关的十分类,但整个数据集支持识别、检测、无监督三种任务,SVHN数据集也因此具有三种不同的benchmark。由于SVHN原始图像都来源于谷歌地球(Google Earth)街景图中的门牌号,其像素信息中自然场景图像的复杂性较高,数字识别难度更大,对识别模型的要求明显也更高。在学术界,当大家已经厌倦MNIST数据集和Fashion-MNIST数据集上99%的准确率时,常常会使用SVHN数据集来验证自己的网络架构在实拍照片上的能力。同时,虽然是实拍数据集,但SVHN识别集的图像被处理得很小(尺寸为32x32,通道为3),样本量也在10万左右,可以在CPU上实现迭代,是非常适合用来走完整流程的数据集。
目前为止,在SVHN数据集识别类benchmark中占据头名的是2020年的宽残差网络WRN28-10,WRN首次将SVHN上的测试准确率推向了99%的水平,同时benchmark上前10的架构全都是在2018年之后提出的。现在,各大论文在SVHN上可以达到的前30名水平大约在97.65%左右。今天我们就基于这样的一个数据集来执行一个完整的流程。
*注意:由于SVHN数据集的测试数据已经被撤下,不再提供下载,因此我们在案例中所使用的“test”集严格来说应该算是验证集。在PyTorch官方的类中,并没有严格区分验证集和测试集,因此我们也使用测试集来称呼我们的test部分数据集。
在课程中,我为大家提供了SVHN数据集的下载链接:
下载解压后,我们在SVHN文件夹中会看到两个mat格式的文件。将该层目录直接放入PyTorch中进行读取,即可顺利读入SVHN数据集中用于识别的部分。可惜的是,由于mat文件无法在win或者mac操作系统中被识别为图片,所以我们无法在操作系统中自由地查看SVHN中的图像,要了解图像,就必须先将图像读入。

1 设置库,导入环境
#配置相关环境
import os
import torch
os.environ['KMP_DUPLICATE_LIB_OK']='True' #用于避免jupyter环境突然关闭
torch.backends.cudnn.benchmark=True #用于加速GPU运算的代码
#导入pytorch一个完整流程所需的可能全部的包
import torchvision
from torch import nn, optim
from torch.nn import functional as F
from torchvision import transforms as T
from torchvision import models as m
from torch.utils.data import DataLoader
#导入作为辅助工具的各类包
import matplotlib.pyplot as plt #可视化
from time import time #计算时间、记录时间
import datetime
import random #控制随机性
import numpy as np
import pandas as pd
import gc #garbage collector 垃圾回收
#设置全局的随机数种子,这些随机数种子只能提供有限的控制
#并不能完全令模型稳定下来
torch.manual_seed(1412) #torch
random.seed(1412) #random
np.random.seed(1412) #numpy.random
#GPU系统会返回True,CPU系统会返回False
torch.cuda.is_available()
#True
#GPU系统会令device = "gpu", cpu系统会令device = "cpu"
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
device
#device(type='cuda')
2 数据导入、数据探索、数据增强
导入库之后,我们将开始导入数据。如果我们的数据集是自己的自定义数据,我们则需要写类
CustomData来进行导入,幸运的是SVHN是PyTorch中提供了接口的数据集,在课程资料中下载后即可使用torchvision.datasets中的类来帮助我们导入。通常在第一次导入图像的时候,我们不会使用数据增强的任何手段,而是直接ToTensor()导入进行查看。
#导入数据
train = torchvision.datasets.SVHN(root ='/Users/zhucan/Desktop/SVHN'
,split ="train"
,download = False
,transform = T.ToTensor()
)
test = torchvision.datasets.SVHN(root ='/Users/zhucan/Desktop/SVHN'
,split ="test"
,download = False
,transform = T.ToTensor())
train
#Dataset SVHN
# Number of datapoints: 73257
# Root location: /Users/zhucan/Desktop/SVHN
# Split: train
# StandardTransform
#Transform: ToTensor()
test
#Dataset SVHN
# Number of datapoints: 26032
# Root location: /Users/zhucan/Desktop/SVHN
# Split: test
# StandardTransform
#Transform: ToTensor()
for x,y in train:
print(x.shape)
print(y)
break #打印其中一个样本
#torch.Size([3, 32, 32])
#1
np.unique(train.labels)
#array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
#让每个数据集随机显示5张图像
def plotsample(data): #只能够接受tensor格式的图像
fig, axs = plt.subplots(1,5,figsize=(10,10)) #建立子图
for i in range(5):
num = random.randint(0,len(data)-1) #首先选取随机数,随机选取五次
#抽取数据中对应的图像对象,make_grid函数可将任意格式的图像的通道数升为3,而不改变图像原始的数据
#而展示图像用的imshow函数最常见的输入格式也是3通道
npimg = torchvision.utils.make_grid(data[num][0]).numpy()
nplabel = data[num][1] #提取标签
#将图像由(3, weight, height)转化为(weight, height, 3),并放入imshow函数中读取
axs[i].imshow(np.transpose(npimg, (1, 2, 0)))
axs[i].set_title(nplabel) #给每个子图加上标签
axs[i].axis("off") #消除每个子图的坐标轴
plotsample(train) #分辨率很低,数据集有一定的难度
plotsample(test)


了解数据集的基本情况之后,我们需要设置正式导入图像的代码之前,并且必须先定义用于处理图像数据的transform。在决定transform时,我们要决定输入特征图的尺寸、是否执行数据增强、使用怎样的数值进行归一化等信息。通常来说,我们会在训练之后再决定是否要使用数据增强,但对于小型数据集或表格数据集,学习力很强的卷积网络往往非常容易过拟合,因此我们会防御性地增加一些数据增强(这个行为可能让模型变得更加不稳定,但同时可以一定程度上防止过拟合)。需要注意的是,数字识别和其他照片识别在“不变性”上会有较大的差异。举个例子,识别水果、动物、交通工具等图像时,随机水平翻转甚至上下翻转可能是一个很好的选择,但对数字和字母识别来说,测试集中原则上不会存在水平、竖直翻转的情况。同理的还有大规模旋转、变形等常见的数据增强手段。不适合的数据增强不仅会让运算变慢,同时还可能拉低模型整体的预测分数,需要格外注意。
#图像太模糊/分辨率太低 - 训练集测试集上都一致
#如果有一些过于清晰的图片,可能反而不好判断
#RandomCrop
#RandomRotation
trainT = T.Compose([T.RandomCrop(28)
,T.RandomRotation(degrees = [-30,30])
,T.ToTensor()
,T.Normalize(mean = [0.485,0.456,0.406]
,std = [0.229,0.224,0.225])])
testT = T.Compose([T.CenterCrop(28)
,T.ToTensor()
,T.Normalize(mean = [0.485,0.456,0.406]
,std = [0.229,0.224,0.225])])
train = torchvision.datasets.SVHN(root ='/Users/zhucan/Desktop/SVHN'
,split ="train"
,download = False
,transform = trainT
)
test = torchvision.datasets.SVHN(root ='/Users/zhucan/Desktop/SVHN'
,split ="test"
,download = False
,transform = testT
)
plotsample(train)

3 基于经典架构构筑自己的网络
#小型数据集 - 比较浅、参数量整体较少
#ResNet18,VGG13/16
#基于小型数据集,首先考虑使用各个经典架构中比较浅、但学习能力又比较强的架构
#比如ResNet18、VGG16、Inception也可以考虑
torch.manual_seed(1412)
resnet18_ = m.resnet18()
vgg16_ = m.vgg16() #VGG本来参数量就很大,因此我个人较少使用vgg16_bn
#32x32 - 2个池化/2个步长为2的卷积层
# (2) + (3) - AlexNet
#查看网络架构,从中选择我们希望使用的部分
#时刻要注意原始架构是在ImageNet数据集上构建的,图像的尺寸、输入、输出都发生了变化
#小图像尺寸意味着池化层/步长为2的卷积层出现的次数有限,惯例来说只能出现2次,最终的特征图尺寸需要是7x7
#输出变化意味着最后的层需要自己写
resnet18_
class MyResNet(nn.Module):
def __init__(self):
super().__init__()
self.block1 = nn.Sequential(nn.Conv2d(3,64,kernel_size=3
,stride=1,padding=1,bias=False)
,resnet18_.bn1
,resnet18_.relu) #删除池化层
#后续的架构直接从经典架构中选
#对尺寸很小的数据集而言,我们的深度本来就不深,因此可以试着在特征图数量上有所增加(增加宽度)
self.block2 = resnet18_.layer2 #2个残差单元
self.block3 = resnet18_.layer3 #2个残差单元
#自适应平均池化+线性层,此处都与残差网络一致
self.avgpool = resnet18_.avgpool
#输出的线性层自己写,以确保输出的类别数量正确
self.fc = nn.Linear(in_features=256, out_features=10, bias=True)
def forward(self,x):
x = self.block1(x)
x = self.block2(x)
x = self.block3(x)
x = self.avgpool(x)
x = x.view(x.shape[0],256)
x = self.fc(x)
return x
vgg16_
[*vgg16_.features[0:9]] #包含了某些对象的对象/generator
#[Conv2d(3, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)),
# ReLU(inplace=True),
# Conv2d(64, 64, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)),
# ReLU(inplace=True),
# MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False),
# Conv2d(64, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)),
# ReLU(inplace=True),
# Conv2d(128, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1)),
# ReLU(inplace=True)]
class MyVgg(nn.Module):
def __init__(self):
super().__init__()
#在9层之后增加一个单独的卷积层,再加入池化层,构成(卷积x2+池化) + (卷积x3+池化)的类似AlexNet的结构
self.features = nn.Sequential(*vgg16_.features[0:9] #星号用于解码
,nn.Conv2d(128, 128, kernel_size=3, stride=1, padding=1)
,nn.ReLU(inplace=True)
,nn.MaxPool2d(2,2, padding=0, dilation=1, ceil_mode=False))
#进入线性层时输入通道数发生变化,因此线性层需要重写
#输出层也需要重写
self.avgpool = vgg16_.avgpool
self.fc = nn.Sequential(nn.Linear(7*7*128, out_features=4096,bias=True)
,*vgg16_.classifier[1:6]
,nn.Linear(in_features=4096, out_features=10,bias=True))
def forward(self,x):
x = self.features(x)
x = self.avgpool(x)
x = x.view(x.shape[0],7*7*128)
x = self.fc(x)
return x
from torchinfo import summary
summary(MyResNet(),(10,3,28,28),depth=2,device="cpu")
# ==========================================================================================
# Layer (type:depth-idx) Output Shape Param #
# ==========================================================================================
# MyResNet -- --
# ├─Sequential: 1-1 [10, 64, 28, 28] --
# │ └─Conv2d: 2-1 [10, 64, 28, 28] 1,728
# │ └─BatchNorm2d: 2-2 [10, 64, 28, 28] 128
# │ └─ReLU: 2-3 [10, 64, 28, 28] --
# ├─Sequential: 1-2 [10, 128, 14, 14] --
# │ └─BasicBlock: 2-4 [10, 128, 14, 14] 230,144
# │ └─BasicBlock: 2-5 [10, 128, 14, 14] 295,424
# ├─Sequential: 1-3 [10, 256, 7, 7] --
# │ └─BasicBlock: 2-6 [10, 256, 7, 7] 919,040
# │ └─BasicBlock: 2-7 [10, 256, 7, 7] 1,180,672
# ├─AdaptiveAvgPool2d: 1-4 [10, 256, 1, 1] --
# ├─Linear: 1-5 [10, 10] 2,570
# ==========================================================================================
# Total params: 2,629,706
# Trainable params: 2,629,706
# Non-trainable params: 0
# Total mult-adds (G): 2.07
# ==========================================================================================
# Input size (MB): 0.09
# Forward/backward pass size (MB): 38.13
# Params size (MB): 10.52
# Estimated Total Size (MB): 48.75
# ==========================================================================================
summary(MyVgg(),(10,3,28,28),depth=2,device="cpu")
# ==========================================================================================
# Layer (type:depth-idx) Output Shape Param #
# ==========================================================================================
# MyVgg -- --
# ├─Sequential: 1-1 [10, 128, 7, 7] --
# │ └─Conv2d: 2-1 [10, 64, 28, 28] 1,792
# │ └─ReLU: 2-2 [10, 64, 28, 28] --
# │ └─Conv2d: 2-3 [10, 64, 28, 28] 36,928
# │ └─ReLU: 2-4 [10, 64, 28, 28] --
# │ └─MaxPool2d: 2-5 [10, 64, 14, 14] --
# │ └─Conv2d: 2-6 [10, 128, 14, 14] 73,856
# │ └─ReLU: 2-7 [10, 128, 14, 14] --
# │ └─Conv2d: 2-8 [10, 128, 14, 14] 147,584
# │ └─ReLU: 2-9 [10, 128, 14, 14] --
# │ └─Conv2d: 2-10 [10, 128, 14, 14] 147,584
# │ └─ReLU: 2-11 [10, 128, 14, 14] --
# │ └─MaxPool2d: 2-12 [10, 128, 7, 7] --
# ├─AdaptiveAvgPool2d: 1-2 [10, 128, 7, 7] --
# ├─Sequential: 1-3 [10, 10] --
# │ └─Linear: 2-13 [10, 4096] 25,694,208
# │ └─ReLU: 2-14 [10, 4096] --
# │ └─Dropout: 2-15 [10, 4096] --
# │ └─Linear: 2-16 [10, 4096] 16,781,312
# │ └─ReLU: 2-17 [10, 4096] --
# │ └─Dropout: 2-18 [10, 4096] --
# │ └─Linear: 2-19 [10, 10] 40,970
# ==========================================================================================
# Total params: 42,924,234
# Trainable params: 42,924,234
# Non-trainable params: 0
# Total mult-adds (G): 1.45
# ==========================================================================================
# Input size (MB): 0.09
# Forward/backward pass size (MB): 14.71
# Params size (MB): 171.70
# Estimated Total Size (MB): 186.50
# ==========================================================================================
#残差网络的参数量少很多,但是总计算量是VGG的两倍还多
#同时,VGG模型占用的内存更大,所以VGG需要更大的显存,但在GPU上VGG理论上应该更快
#在这个过程中,我们是从已经实例化的类中直接复制层来使用
#因此我们复用经典架构的部分,参数已经被实例化好了
#因此实例化具体的MyResNet()时没有参数生成
[*MyResNet().block2[0].parameters()][0][0][0] #复制的部分参数是一致的
#tensor([[ 0.0324, -0.0175, 0.0459],
# [ 0.0728, -0.0392, 0.0903],
# [-0.0266, -0.0177, -0.0227]], grad_fn=<SelectBackward>)
[*resnet18_.layer2[0].conv1.parameters()][0][0][0]
#tensor([[ 0.0324, -0.0175, 0.0459],
# [ 0.0728, -0.0392, 0.0903],
# [-0.0266, -0.0177, -0.0227]], grad_fn=<SelectBackward>)
#没有复用经典架构的部分,则在我们实例化网络的时候才有参数
[*resnet18_.fc.parameters()] #自己设立的部分参数是不同的
[*MyResNet().fc.parameters()]
# [Parameter containing:
# tensor([[ 0.0218, -0.0385, -0.0548, ..., 0.0045, -0.0612, 0.0406],
# [-0.0398, 0.0063, 0.0567, ..., -0.0390, 0.0392, -0.0345],
# [-0.0231, -0.0487, -0.0456, ..., -0.0538, 0.0066, -0.0088],
# ...,
# [ 0.0070, -0.0560, -0.0430, ..., 0.0526, -0.0575, 0.0610],
# [-0.0354, -0.0283, 0.0108, ..., -0.0044, -0.0565, 0.0460],
# [ 0.0033, 0.0593, 0.0278, ..., -0.0409, -0.0437, 0.0202]],
# requires_grad=True),
# Parameter containing:
# tensor([-0.0122, -0.0585, 0.0398, -0.0387, 0.0612, -0.0471, 0.0494, 0.0117,
# 0.0264, 0.0493], requires_grad=True)]
从结构上来看,VGG天生就比残差网络劣势一些:在两个池化层/步长为2的卷积层之间,残差网络可以利用残差快提供更多的卷积层。在我们的架构中,拥有两个大Layers的残差网络拥有9个卷积层,而对于仅仅使用普通的卷积层堆叠的VGG来说,在参数量高于残差网络2倍的前提下,却只能拥有5个卷积层。
4 一套完整的训练函数
4.1 迭代与预测
def IterOnce(net,criterion,opt,x,y):
"""
对模型进行一次迭代的函数
net: 实例化后的架构
criterion: 损失函数
opt: 优化算法
x: 这一个batch中所有的样本
y: 这一个batch中所有样本的真实标签
"""
sigma = net.forward(x)
loss = criterion(sigma,y)
loss.backward()
opt.step()
opt.zero_grad(set_to_none=True) #比起设置梯度为0,让梯度为None会更节约内存
yhat = torch.max(sigma,1)[1]
correct = torch.sum(yhat == y)
return correct,loss
def TestOnce(net,criterion,x,y):
"""
对一组数据进行测试并输出测试结果的函数
net: 经过训练后的架构
criterion:损失函数
x:要测试的数据的所有样本
y:要测试的数据的真实标签
"""
#对测试,一定要阻止计算图追踪
#这样可以节省很多内存,加速运算
with torch.no_grad():
sigma = net.forward(x)
loss = criterion(sigma,y)
yhat = torch.max(sigma,1)[1]
correct = torch.sum(yhat == y)
return correct,loss
4.2 提前停止
优化算法以寻找损失函数的全局最小值作为目的,理想状态下,当算法找到了全局最优时神经网络就“收 敛”了,迭代就会停止。然而遗憾的是,我们并不知道真正的全局最小值是多少,所以无法判断算法是否真正找到了全局最小值。其次,一种经常发生的情况可可能是,算法真实能够获取的局部最小值为0.5,且优化算法可能在很短的时间内就锁定了(0.500001, 0.49999)之间的范围,但由于学习率等超参数的设置问题,始终无法到达最小值0.5。这两种情况下优化算法都会持续(无效地)迭代下去,因此我们会需要人为来停止神经网络。我们只会在两种情况下停止神经网络的迭代:
- 神经网络已经达到了足够好的效果(非常接近收敛状态),持续迭代下去不会有助于算法效果,比如说,会陷入过拟合,或者会让模型停滞不前
- 神经网络的训练时间太长了,即便我们知道它还没有找到最优结果
这两种情况中的第二种非常容易理解,就是我们设置epochs来控制迭代次数,当所有的epochs都循环完毕,迭代自动也就停止了。在卷积训练的时候,我们通常会设置较小的epochs先尝试一下,如果算法往正确的方向迭代,我们才会设置更大的epochs来继续迭代。数据量巨大的时候我们常使用这样的方法来避免算法进入几天几夜的训练流程、最终却得到糟糕的结果。
第一种情况就比较复杂了。首先,我们必须先定义什么是”足够好的效果”。就像我们之前提过多次的,神经网络通过降低损失函数上的值来求解参数
w
w
w和
b
b
b,所以只要损失函数的值持续减小、或验证集上的分数持续上升,我们就可以认为神经网络的效果还有提升的空间。在实际的训练流程中,刚开始训练神经网络时,测试集和训练集上的损失一般都很高(有时,训练集上的损失比测试集上的损失还高),但随着训练次数的增多,两种损失都会开始快速下降,一般训练集下降得更快,测试集下降得缓慢一些。直到某一次迭代时,无论我们如何训练,测试集上的损失都不再下降,甚至开始升高,此时我们就需要让迭代停下。当测试集上的损失不再下降、持续保持平稳时,继续训练会浪费训练资源,迭代下去模型也会停滞不前,因此需要停止。当测试集上的损失开始升高时,往往训练集上的损失还是在稳步下降,继续迭代下去就会造成训练集损失比测试集损失小很多的情况,也就是过拟合。在过拟合之前及时停止,能够防止模型被迭代到过拟合状况下。
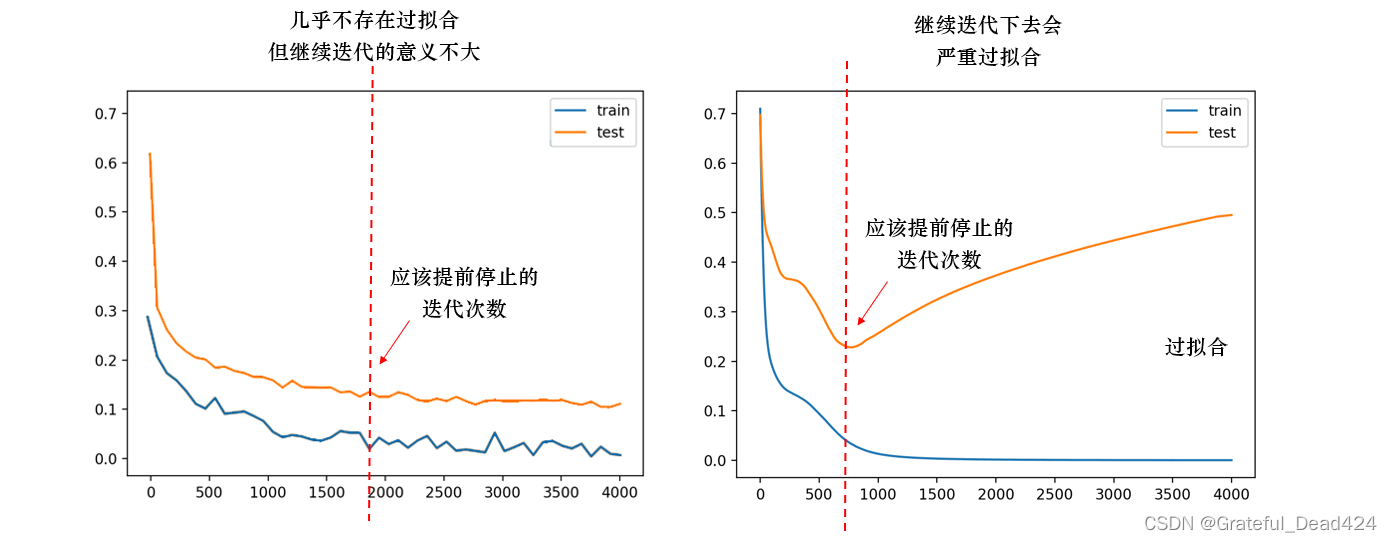
那我们如何找到这个测试集损失不再下降、准确率不再上升的“某一时间点”呢?此时,我们可以规定一个阈值,例如,当连续
n
n
n次迭代中,损失函数的减小值都低于阈值tol,或者测试集的分数提升值都低于阈值tol的时候,我们就可以令迭代停止了。此时,即便我们规定的epochs还没有被用完,我们也可以认为神经网络已经非常接近“收敛”,可以将神经网络停下了。这种停止在机器学习中被称为“early stopping”。有时候,学习率衰减也可能会与early stopping结合起来。在有的神经网络中,我们或许会规定,当连续 次迭代中损失函数的减小值都低于阈值tol时,将学习率进行衰减。当然,如果我们使用的优化算法中本来就带有学习率衰减的机制,那我们则不需要考虑这点了。
在实际实现提前停止的时候,我们规定连续 n n n次是连续5次(如果你愿意,可以设计这个值为超参数)。同时,损失函数的减小值并不是在这一轮迭代和上一轮迭代中进行比较,我们需要让本轮迭代的损失与历史迭代最小损失比较,如果历史最小损失 - 本轮迭代的损失 > tol,我们才认可损失函数减小了。这种设置对于不稳定的架构不太友好,如果我们发现模型不稳定,则可以设置较小的阈值。基于这个思路,来看具体的代码:
class EarlyStopping():
def __init__(self, patience = 5, tol = 0.0005): #惯例地定义我们所需要的一切变量/属性\
#当连续patience次迭代时,这一轮迭代的损失与历史最低损失之间的差值小于阈值时
#就触发提前停止
self.patience = patience
self.tol = tol #tolerance,累积5次都低于tol才会触发停止
self.counter = 0 #计数,计算现在已经累积了counter次
self.lowest_loss = None
self.early_stop = False #True - 提前停止,False - 不要提前停止
def __call__(self,val_loss):
if self.lowest_loss == None: #这是第一轮迭代
self.lowest_loss = val_loss
elif self.lowest_loss - val_loss > self.tol:
self.lowest_loss = val_loss
self.counter = 0
elif self.lowest_loss - val_loss < self.tol:
self.counter += 1
print("\t NOTICE: Early stopping counter {} of {}".format(self.counter,self.patience))
if self.counter >= self.patience:
print('\t NOTICE: Early Stopping Actived')
self.early_stop = True
return self.early_stop
#这一轮迭代的损失与历史最低损失之间的差 - 阈值
4.3 训练、测试、监控、保存权重、绘图
在这个函数中,我们将整合之前所写的全部内容,并将训练、测试、监控、保存权重等流程全部包含在同一个函数中。这个函数是基于我们在Lesson11时所写的那个非常简单的训练函数所进行的拓展,其基本思路与之前的函数相似,但在之前的函数上增加了非常多基于现实因素的考虑。
def fit_test(net,batchdata,testdata,criterion,opt,epochs,tol,modelname,PATH):
"""
对模型进行训练,并在每个epoch后输出训练集和测试集上的准确率/损失
以实现对模型的监控
实现模型的保存
参数说明:
net: 实例化后的网络
batchdata:使用Dataloader分割后的训练数据
testdata:使用Dataloader分割后的测试数据
criterion:所使用的损失函数
opt:所使用的优化算法
epochs:一共要使用完整数据集epochs次
tol:提前停止时测试集上loss下降的阈值,连续5次loss下降不超过tol就会触发提前停止
modelname:现在正在运行的模型名称,用于保存权重时作为文件名
PATH:将权重文件保存在path目录下
"""
SamplePerEpoch = batchdata.dataset.__len__() #整个epoch里有多少个样本
allsamples = SamplePerEpoch*epochs
trainedsamples = 0
trainlosslist = []
testlosslist = []
early_stopping = EarlyStopping(tol=tol)
highestacc = None
for epoch in range(1,epochs+1):
net.train()
correct_train = 0
loss_train = 0
for batch_idx, (x, y) in enumerate(batchdata):
y = y.view(x.shape[0])
correct, loss = IterOnce(net,criterion,opt,x,y)
trainedsamples += x.shape[0]
loss_train += loss
correct_train += correct
if (batch_idx+1) % 125 == 0:
#现在进行到了哪个epoch
#现在训练到了多少个样本
#总共要训练多少个样本
#现在的训练的样本占总共需要训练的样本的百分比
print('Epoch{}:[{}/{}({:.0f}%)]'.format(epoch
,trainedsamples
,allsamples
,100*trainedsamples/allsamples))
TrainAccThisEpoch = float(correct_train*100)/SamplePerEpoch
TrainLossThisEpoch = float(loss_train*100)/SamplePerEpoch #平均每个样本上的损失
trainlosslist.append(TrainLossThisEpoch)
#每次训练完一个epoch,就在测试集上验证一下模型现在的效果
net.eval()
loss_test = 0
correct_test = 0
loss_test = 0
TestSample = testdata.dataset.__len__()
for x,y in testdata:
y = y.view(x.shape[0])
correct, loss = TestOnce(net,criterion,x,y)
loss_test += loss
correct_test += correct
TestAccThisEpoch = float(correct_test * 100)/TestSample
TestLossThisEpoch = float(loss_test * 100)/TestSample
testlosslist.append(TestLossThisEpoch)
#对每一个epoch,打印训练和测试的结果
#训练集上的损失,测试集上的损失,训练集上的准确率,测试集上的准确率
print("\t Train Loss:{:.6f}, Test Loss:{:.6f}, Train Acc:{:.3f}%, Test Acc:{:.3f}%".format(TrainLossThisEpoch
,TestLossThisEpoch
,TrainAccThisEpoch
,TestAccThisEpoch))
#如果测试集准确率出现新高/测试集loss出现新低,那我会保存现在的这一组权重
if highestacc == None: #首次进行测试
highestacc = TestAccThisEpoch
if highestacc < TestAccThisEpoch:
highestacc = TestAccThisEpoch
torch.save(net.state_dict(),os.path.join(PATH,modelname+".pt"))
print("\t Weight Saved")
#提前停止
early_stop = early_stopping(TestLossThisEpoch)
if early_stop == "True":
break
print("Complete")
return trainlosslist, testlosslist
def full_procedure(net,epochs,bs,modelname, PATH, lr=0.001,alpha=0.99,gamma=0,wd=0,tol=10**(-5)):
torch.manual_seed(1412)
#分割数据
batchdata = DataLoader(train,batch_size=bs,shuffle=True
,drop_last=False,num_workers = 4) #线程 - 调度计算资源的最小单位
testdata = DataLoader(test,batch_size=bs,shuffle=False
,drop_last=False,num_workers = 4)
#损失函数,优化算法
criterion = nn.CrossEntropyLoss(reduction="sum") #进行损失函数计算时,最后输出结果的计算模式
opt = optim.RMSprop(net.parameters(),lr=lr
,alpha=alpha,momentum=gamma,weight_decay=wd)
#训练与测试
trainloss, testloss = fit_test(net,batchdata,testdata,criterion,opt,epochs,tol,modelname,PATH)
return trainloss, testloss
#绘图函数
def plotloss(trainloss, testloss):
plt.figure(figsize=(10, 7))
plt.plot(trainloss, color="red", label="Trainloss")
plt.plot(testloss, color="orange", label="Testloss")
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()
在这里,需要对num_worker与pin_memory两个参数进行一下特别说明。num_workers很容易理解,它代表允许CPU运行的线程数,num_workers越高,CPU上并行的线程就越多,计算就越快。
pin_memory则控制是否将生成的数据放置在锁页内存中。在计算机中,内存是运行程序的空间,硬盘(又叫虚拟内存)是储存文件的空间。通常来说,当内存不够用时,计算机会向硬盘“借用”一些空间来支持程序的裕兴,此时数据和程序需要在内存与硬盘之间交换,程序运行的速度就会减慢。如果不希望硬盘与内存进行交换,我们可以设置“锁页内存”。锁页内存中的资源只允许在内存中存放,不允许借用硬盘资源。当内存资源比较充足时,我们可以设置pin_memory=True,让生成的tensor都属于锁页内存。在这个模式下,锁页内存中的tensor与程序都不需要与硬盘进行交互,在CPU运行时更快,转义到GPU上的速度也会更快,这可以极大程度地加速整个运算流程。然而,当内存资源不足时,设置pin_memory=True可能会出现大量警告。我们可以根据自己的硬件来调整这个参数,pin_memory能够发挥的效果与电脑硬件性能有很大的关系。
4.4 完整函数的GPU版
torch.cuda.manual_seed(1412)
torch.cuda.manual_seed_all(1412)
torch.cuda.is_available()
device = torch.device("cuda")
def fit_test(net,batchdata,testdata,criterion,opt,epochs,tol,modelname,PATH):
"""
对模型进行训练,并在每个epoch后输出训练集和测试集上的准确率/损失
以实现对模型的监控
实现模型的保存
参数说明:
net: 实例化后的网络
batchdata:使用Dataloader分割后的训练数据
testdata:使用Dataloader分割后的测试数据
criterion:所使用的损失函数
opt:所使用的优化算法
epochs:一共要使用完整数据集epochs次
tol:提前停止时测试集上loss下降的阈值,连续5次loss下降不超过tol就会触发提前停止
modelname:现在正在运行的模型名称,用于保存权重时作为文件名
PATH:将权重文件保存在path目录下
"""
SamplePerEpoch = batchdata.dataset.__len__() #整个epoch里有多少个样本
allsamples = SamplePerEpoch*epochs
trainedsamples = 0
trainlosslist = []
testlosslist = []
early_stopping = EarlyStopping(tol=tol)
highestacc = None
for epoch in range(1,epochs+1):
net.train()
correct_train = 0
loss_train = 0
for batch_idx, (x, y) in enumerate(batchdata):
#non_blocking 非阻塞 = True
x = x.to(device,non_blocking=True)
y = y.to(device,non_blocking=True).view(x.shape[0])
correct, loss = IterOnce(net,criterion,opt,x,y)
#计算样本总量、总的correct、loss
trainedsamples += x.shape[0]
loss_train += loss
correct_train += correct
if (batch_idx+1) % 125 == 0:
#现在进行到了哪个epoch
#现在训练到了多少个样本
#总共要训练多少个样本
#现在的训练的样本占总共需要训练的样本的百分比
print('Epoch{}:[{}/{}({:.0f}%)]'.format(epoch
,trainedsamples
,allsamples
,100*trainedsamples/allsamples))
TrainAccThisEpoch = float(correct_train*100)/SamplePerEpoch
TrainLossThisEpoch = float(loss_train*100)/SamplePerEpoch #平均每个样本上的损失
trainlosslist.append(TrainLossThisEpoch)
#清理GPU内存
#清理掉一个epoch循环下面不再需要的中间变量
del x,y,correct,loss,correct_train,loss_train #删除数据与变量
gc.collect() #清除数据与变量相关的缓存
torch.cuda.empty_cache() #缓存分配器分配出去的内存给释放掉
#每次训练完一个epoch,就在测试集上验证一下模型现在的效果
net.eval()
loss_test = 0
correct_test = 0
loss_test = 0
TestSample = testdata.dataset.__len__()
for x,y in testdata:
x = x.to(device, non_blocking=True)
y = y.to(device,non_blocking=True).view(x.shape[0])
correct, loss = TestOnce(net,criterion,x,y)
loss_test += loss
correct_test += correct
TestAccThisEpoch = float(correct_test * 100)/TestSample
TestLossThisEpoch = float(loss_test * 100)/TestSample
testlosslist.append(TestLossThisEpoch)
#清理GPU内存
del x,y,correct,loss,correct_test,loss_test
gc.collect()
torch.cuda.empty_cache()
#对每一个epoch,打印训练和测试的结果
#训练集上的损失,测试集上的损失,训练集上的准确率,测试集上的准确率
print("\t Train Loss:{:.6f}, Test Loss:{:.6f}, Train Acc:{:.3f}%, Test Acc:{:.3f}%".format(TrainLossThisEpoch
,TestLossThisEpoch
,TrainAccThisEpoch
,TestAccThisEpoch))
#如果测试集准确率出现新高/测试集loss出现新低,那我会保存现在的这一组权重
if highestacc == None: #首次进行测试
highestacc = TestAccThisEpoch
if highestacc < TestAccThisEpoch:
highestacc = TestAccThisEpoch
torch.save(net.state_dict(),os.path.join(PATH,modelname+".pt"))
print("\t Weight Saved")
#提前停止
early_stop = early_stopping(TestLossThisEpoch)
if early_stop == "True":
break
print("Complete")
return trainlosslist, testlosslist
#GPU内存优化管理机制 - 缓存内存分配器(torch帮助gpu)
#数据x - 80,分配给它100字节的资源,20字节空闲
#80 - 张量内存
#20 - 缓存分配器指定的更多的缓存
#GPU - 使用了100字节的资源
#del 张量内存
#torch.cuda.empty_cache() 缓存分配器指定的那些缓存
#GPU显存进行监控的时候
torch.cuda.memory_allocated() #张量内存的占用情况(现状) 80
torch.cuda.memory_reserved() #缓存分配器占用的所有内存(现状) 100
torch.cuda.max_memory_allocated() #自GPU运行以来占用过的最大张量内存(峰值)
#我们通常会依赖的内存显示
nvidia-smi #显存占用率和gpu使用率
def full_procedure(net,epochs,bs,modelname, PATH, lr=0.001,alpha=0.99,gamma=0,wd=0,tol=10**(-5)):
torch.cuda.manual_seed(1412)
torch.cuda.manual_seed_all(1412)
torch.manual_seed(1412)
#分割数据
batchdata = DataLoader(train,batch_size=bs,shuffle=True
,drop_last=False,pin_memory=True)
testdata = DataLoader(test,batch_size=bs,shuffle=False
,drop_last=False,pin_memory=True)
#损失函数,优化算法
criterion = nn.CrossEntropyLoss(reduction="sum") #进行损失函数计算时,最后输出结果的计算模式
opt = optim.RMSprop(net.parameters(),lr=lr
,alpha=alpha,momentum=gamma,weight_decay=wd)
#训练与测试
trainloss, testloss = fit_test(net,batchdata,testdata,criterion,opt,epochs,tol,modelname,PATH)
return trainloss, testloss
#pin_memory 控制是否将生成的数据放置在锁页内存当中
#内存 - 程序运行的空间 - 8G,16G,24G
#硬盘(虚拟内存) - 储存文件的空间 - 2T,5T,1G,1T
#“锁页内存” - 只能在内存中存放,不允许与硬盘进行交换的程序/数据
#pin_memory = True - 保证你的内存资源比较充足
5 模型选择
当所有准备工作都完成后,我们开始进入模型选择的阶段。在这里我们让两个不同的架构分别运行5次,每次迭代3个epochs,以此来观察两个架构的稳定性及潜力。在有足够算力的情况下,我们可以运行更多次、或者更多的epochs,一般来说,能够在每个架构上运行5次,每次5+epochs是最保险的情况。
#衡量深度学习模型表现————效果、运算速度(效率)、潜力
#效果 - 模型的泛化能力(偏差、方差) 准确率要高、模型要稳定 - 我们需要对同一个架构进行多次训练来衡量方差
#运算速度 - 看模型运行的时间
#潜力 - 起点(前几个epochs上能够达到的效果),过拟合(通过调参来抑制过拟合)、欠拟合(加深你的架构)
#在每一个架构上,分别运行3个epochs,运行5次
#回顾模型
from torchinfo import summary
for name,i in[("ResNet",MyResNet()),("VGG",MyVgg())]:
print("\n")
print(name)
print(summary(i,input_size=(10,3,28,28),depth=2,device="cpu"))
print("\n")
# ResNet
# ==========================================================================================
# Layer (type:depth-idx) Output Shape Param #
# ==========================================================================================
# ├─Sequential: 1-1 [10, 64, 28, 28] --
# | └─Conv2d: 2-1 [10, 64, 28, 28] 1,728
# | └─BatchNorm2d: 2-2 [10, 64, 28, 28] 128
# | └─ReLU: 2-3 [10, 64, 28, 28] --
# ├─Sequential: 1-2 [10, 128, 14, 14] --
# | └─BasicBlock: 2-4 [10, 128, 14, 14] 230,144
# | └─BasicBlock: 2-5 [10, 128, 14, 14] 295,424
# ├─Sequential: 1-3 [10, 256, 7, 7] --
# | └─BasicBlock: 2-6 [10, 256, 7, 7] 919,040
# | └─BasicBlock: 2-7 [10, 256, 7, 7] 1,180,672
# ├─AdaptiveAvgPool2d: 1-4 [10, 256, 1, 1] --
# ├─Linear: 1-5 [10, 10] 2,570
# ==========================================================================================
# Total params: 2,629,706
# Trainable params: 2,629,706
# Non-trainable params: 0
# Total mult-adds (G): 14.22
# ==========================================================================================
# Input size (MB): 0.09
# Forward/backward pass size (MB): 32.11
# Params size (MB): 10.52
# Estimated Total Size (MB): 42.73
# ==========================================================================================
# VGG
# ==========================================================================================
# Layer (type:depth-idx) Output Shape Param #
# ==========================================================================================
# ├─Sequential: 1-1 [10, 128, 7, 7] --
# | └─Conv2d: 2-1 [10, 64, 28, 28] 1,792
# | └─ReLU: 2-2 [10, 64, 28, 28] --
# | └─Conv2d: 2-3 [10, 64, 28, 28] 36,928
# | └─ReLU: 2-4 [10, 64, 28, 28] --
# | └─MaxPool2d: 2-5 [10, 64, 14, 14] --
# | └─Conv2d: 2-6 [10, 128, 14, 14] 73,856
# | └─ReLU: 2-7 [10, 128, 14, 14] --
# | └─Conv2d: 2-8 [10, 128, 14, 14] 147,584
# | └─ReLU: 2-9 [10, 128, 14, 14] --
# | └─Conv2d: 2-10 [10, 128, 14, 14] 147,584
# | └─ReLU: 2-11 [10, 128, 14, 14] --
# | └─MaxPool2d: 2-12 [10, 128, 7, 7] --
# ├─AdaptiveAvgPool2d: 1-2 [10, 128, 7, 7] --
# ├─Sequential: 1-3 [10, 10] --
# | └─Linear: 2-13 [10, 4096] 25,694,208
# | └─ReLU: 2-14 [10, 4096] --
# | └─Dropout: 2-15 [10, 4096] --
# | └─Linear: 2-16 [10, 4096] 16,781,312
# | └─ReLU: 2-17 [10, 4096] --
# | └─Dropout: 2-18 [10, 4096] --
# | └─Linear: 2-19 [10, 10] 40,970
# ==========================================================================================
# Total params: 42,924,234
# Trainable params: 42,924,234
# Non-trainable params: 0
# Total mult-adds (G): 6.22
# ==========================================================================================
# Input size (MB): 0.09
# Forward/backward pass size (MB): 14.71
# Params size (MB): 171.70
# Estimated Total Size (MB): 186.50
# ==========================================================================================
#建立目录用于存储模型选择结果
PATH = "/Users/zhucan/Desktop/ModelSelection"
#使用函数full_procedure中的默认参数,在模型选择时加入时间计算
#基于现有显存,batch_size被设置为256,对于CPU而言最好从64开始设置
#MyResNet
avgtime = [] #用来存放每次循环之后获得的训练时间
for i in range(5): #进行5次训练
#设置随机数种子
torch.manual_seed(1412)
#实例化
resnet18_ = m.resnet18()
net = MyResNet().to(device,non_blocking=True)
#训练
start = time() #计算训练时间
trainloss, testloss = full_procedure(net,epochs=3, bs=256
,modelname="model_seletion_resnet"
,PATH = PATH)
avgtime.append(time()-start)
#循环完毕之后记得删除网络,清GPU内存
del net
gc.collect()
torch.cuda.empty_cache()
print(np.mean(avgtime))
#MyVGG
avgtime = []
for i in range(5):
torch.manual_seed(1412)
vgg16_ = m.vgg16_bn()
net = MyVgg().to(device,non_blocking=True)
start = time() #计算训练时间
#此时使用的是full_procedure的默认参数
trainloss, testloss = full_procedure(net,epochs=3, bs=256
,modelname="model_seletion_vgg"
,PATH = PATH)
avgtime.append(time()-start)
del net
gc.collect()
torch.cuda.empty_cache()
print(np.mean(avgtime))
首先在GPU上运行,来看残差网络:

再来看VGG:

从评估结果来看,虽然SVHN数据集尺寸小、数据量也不多,但要达到其benchmark上所展示的结果,还是需要一些技巧和较长的训练时间,要知道在Fashion-MNIST数据集上,即便使用类似于现在的MyVGG的结构,也能够轻易达到大约85%左右的起点。而在现有架构上,残差网络和VGG都有各自的问题。
- 偏差
首先来评估模型在准确率上的表现。从前3个epochs的结果来看,残差网络的起点明显比VGG高很多,经过一个epoch,残差网络在训练集上基本能够达到45%以上的准确率,但VGG最高只能达到32%,大部分时候都在25%徘徊。从损失上看,VGG首次迭代时损失总是奇高无比,残差网络在训练集上的损失相对稳定。3个epochs后,几乎每轮迭代中,残差网络在训练集上能够达到的水平一路走高,基本会超出VGG大约10%以上,但测试集上的表现两者相差不多,都在75%~85%之间徘徊。现在的结果说明MyVgg类表现出来的学习能力不足,残差网络表现出来的学习能力较强,但是泛化能力上两者不分伯仲。
- 方差
残差网络在训练集上的表现基本稳定,不仅每次训练时都一路走高,并且3个epochs后得到的结果比较相似,但在测试集上就是疯狂跳舞,5次训练中有4次都出现了测试集表现“先高再低”的情况,并且都在第三个epoch处就触发了第一次"提前停止"的阈值,这可能意味着模型在测试集上的表现高度不稳定。VGG同样在训练集上一路走高,但3个epochs之后得到的准确率上下存在8%-10%的波动,这一点在测试集上也表现了出来。从结果来看,两个架构的都不太稳定,但VGG比残差网络更不稳定。
- 过拟合与欠拟合
模型是否过拟合需要在大量迭代之后才能观察出来,因为训练前期训练集与测试集的损失都很高,即便训练集的损失比测试集的损失低一些,也不能说明模型过拟合,因此通常在3个epochs下是看不出什么趋势的。不过根据经验,残差网络的过拟合可能是一个潜在的问题,毕竟残差网络是学习能力十分强大的网络,而我们现在所使用的数据集是小数据集。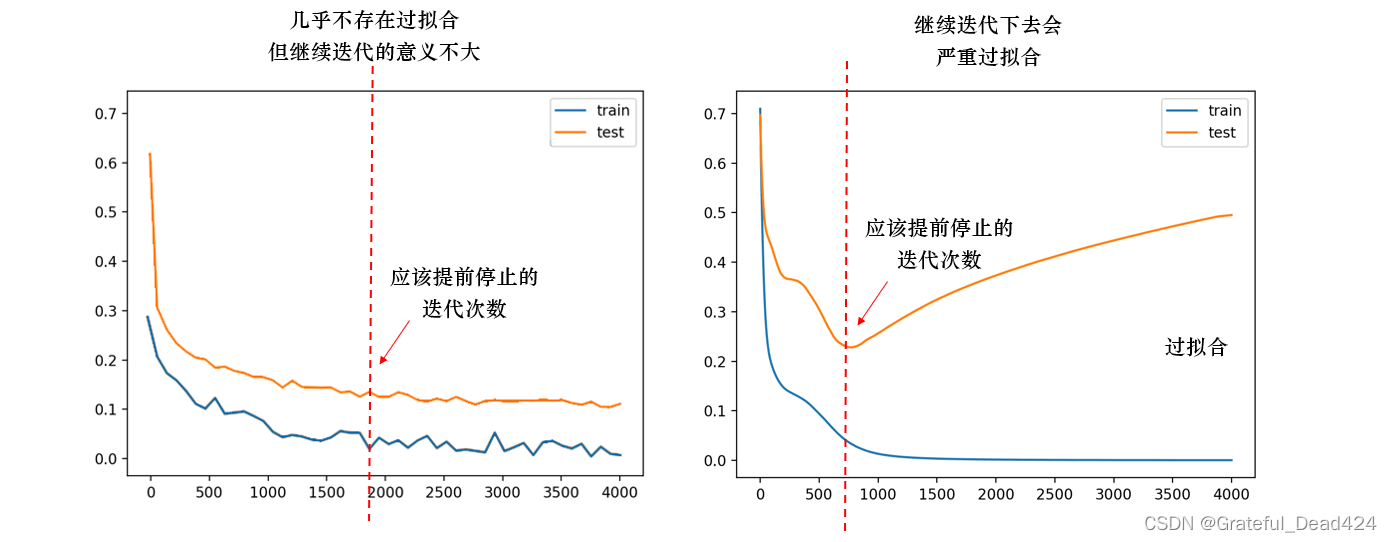
- 效率
从运行结果中时间的记录来看,残差网络与VGG在GPU上的计算速度基本相当,两者差异不大。在CPU上我们也做了1个epoch的实验,残差网络明显比VGG计算更快,表现更好:

到这里,我们基本上已经可以确定模型继续下去的方向了——残差网络现在有更好的基础,我们可以继续训练下去进行观察。对VGG架构而言,目前来看最有效的方向可能是加深网络,比如将5个卷积层增加到8个,但这样会要求更多的算力和时间。在课程中,我们将就残差网络继续调优下去,但我衷心建议大家可以尝试继续加深VGG来进行探索,很有可能VGG会展现出比残差网络更稳定的结果。
6 模型调优
基于自定义的残差网络,我们来进行模型的调优。模型调优与机器学习中的模型调参类似,但又不太相同。模型调参是通过改变参数来左右模型的表现,但深度学习架构本身带有一些随机性、数据处理也带有随机性、就连复现网络结果都非常困难,更不要提试图通过参数去极大地影响模型的表现,所以模型调优更多是在神经网络上不断尝试、观察现象并被动地做出调整的过程。在这个过程中,我们基本遵循一下思路:
- 1、首先增加迭代次数,观察训练集和测试集上的损失是否都呈现为下降趋势
- 2、如果呈现下降趋势,则需要增加训练次数,把模型训练至测试集的损失不再下降为止(触发提前停止) 如果不呈现下降趋势(欠拟合),可能需要立刻更换架构,直到损失呈现下降趋势为止
- 3、当测试集损失不再下降时,停止训练并观察模型的情况,针对现存的问题对症下药 例如,模型过拟合,就采取防止过拟合的操作。模型不稳定,就分析具体原因,让模型变得稳定。
- 4、如果“对症下药”的所有操作不能够再次提升测试集上的准确率则必须考虑重做数据上的特征工程、引入论文中的各项技术、或更换更强大的架构
现在我们的残差网络才刚被训练过3个epochs,除了起点高之外几乎看不出趋势。因此我们需要迭代更多的迭代次数,来观察模型的学习能力。
6.1 更多迭代次数
首先,我们就刚才选出的架构试着迭代10个epochs。
#尝试增加到10个epochs
PATH = "/Users/zhucan/Desktop/ModelSelection"
modelname = "myResNet_test0"
print(modelname)
torch.manual_seed(1412)
resnet18_ = m.resnet18()
net = MyResNet().to(device,non_blocking=True)
start = time() #计算训练时间
trainloss, testloss = full_procedure(net,epochs=10, bs=256
,modelname=modelname
,PATH = PATH)
print(time()-start)
plotloss(trainloss,testloss)
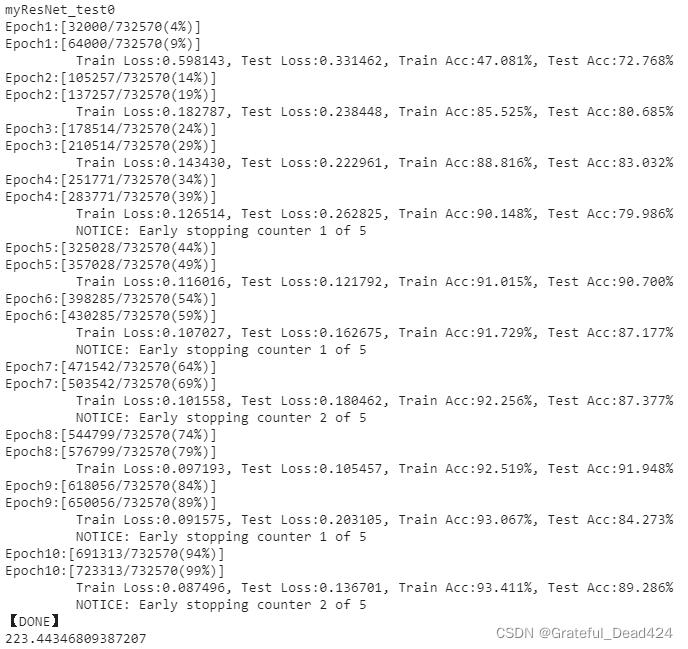
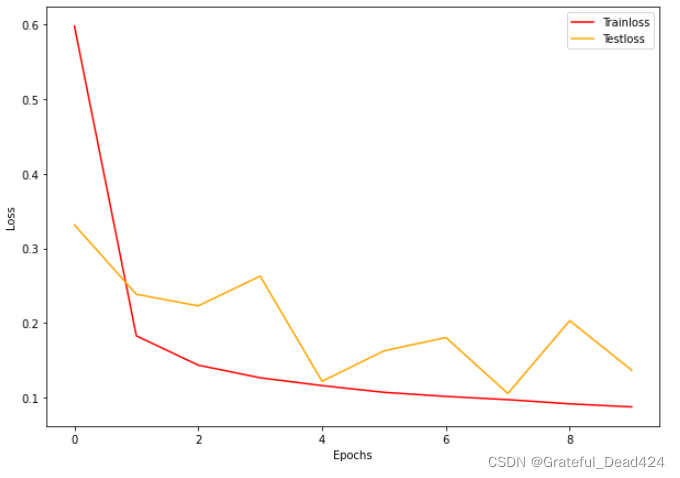
从训练集的结果来看,残差网络持续在进行学习,并且随着epochs的升高,训练集上的准确率有提升到95%以上的可能,测试集虽然高度不稳定,但整体还是呈现下降的趋势。过拟合问题存在,但并不严重。测试集上不稳定的问题可能会随着模型训练次数的增加而缓解,过拟合问题也类似,于是在将降低提前停止阈值设置为
1
0
?
10
10^{-10}
10?10、其他参数不变的基础上,我连续了训练了三次(test1,test2,test3),每次30个epochs,以此来逼近现在模型的极限。
#调小提前停止阈值,再进行三次训练,每次30个epochs
PATH = "/Users/zhucan/Desktop/ModelSelection"
for modelname in ["MyResNet_test1","MyResNet_test2","MyResNet_test3"]:
print(modelname)
torch.manual_seed(1412)
resnet18_ = m.resnet18()
net = MyResNet().to(device,non_blocking=True)
start = time() #计算训练时间
trainloss, testloss = full_procedure(net,epochs=30, bs=256
,modelname=modelname
,PATH = PATH
,tol = 10**(-10))
print(time()-start)
plotloss(trainloss,testloss)
理想的情况是,我们会训练到测试集上的损失下降小于
1
0
?
10
10^{-10}
10?10为止。训练得到的结果如下: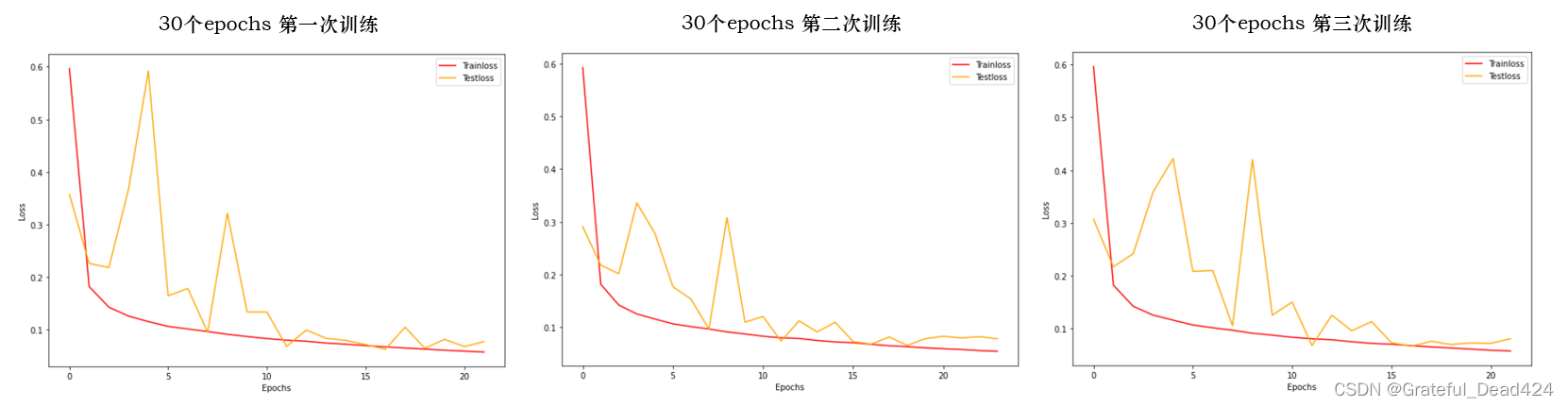
遗憾的是,没有一次训练完成了30个epochs,所有训练都在20+epochs处触发了提前停止。在如此低的提前停止阈值下不能完成30个epochs,说明30个epochs之内模型的泛化能力已经触底。从图像趋势上来看,前期激烈的损失波动确实有些惊人,但随着模型迭代,测试集上的损失确实变得相对稳定了。然而,测试集上的损失并没有形成稳定下降的趋势,而已经开始出现了升高的趋势,这说明继续训练下去,模型会朝着过拟合的方向发展,假设我们继续将阈值调低,模型被允许继续训练,测试集的损失可能会开始走高。
第一次训练最后5个epochs的结果:
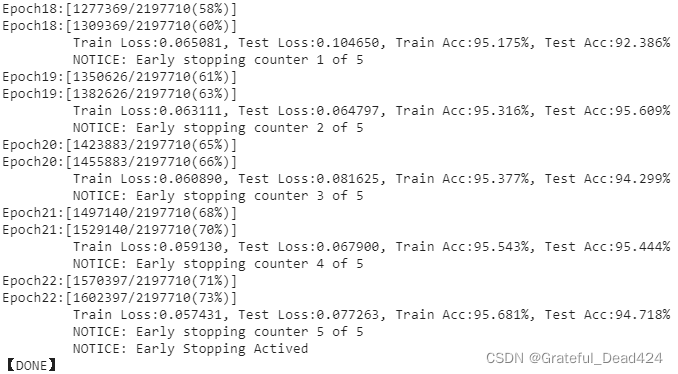
第二次训练最后5个epochs:
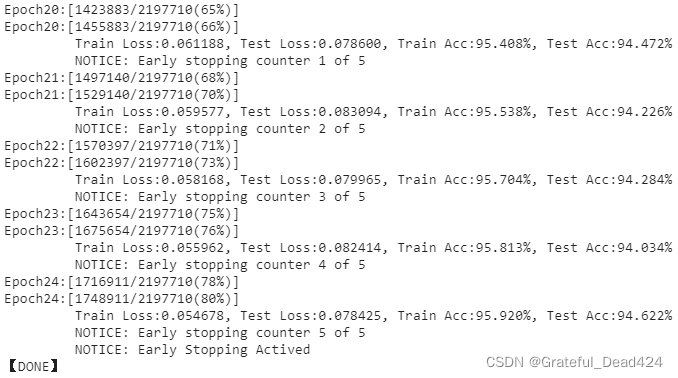
第三次训练最后5个epochs:
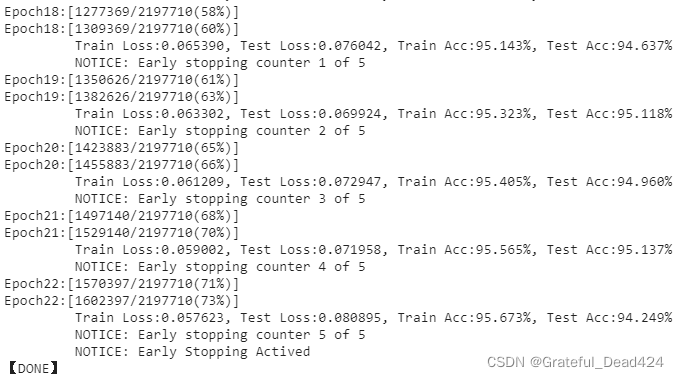
再来看准确率。在经过20个epochs之后,训练集还在稳步缓慢的上升中,但测试集的准确率基本徘徊在94%~95%之间不再提升。在这个架构和这一组参数下,测试集的准确率可以被认为已经达到天花板。现在我们必须从架构和参数上寻求突破,力求打破现在的瓶颈,让测试集准确率继续上升。但调整架构和调整参数是完全不同的操作,两种手段各有利弊——
- 1、调整架构意味着我们否定现有模型的学习能力和潜力,之前的训练全部作废,必须从0开始训练模型。如果你有GPU资源、或者你的数据集比较小,我们或许可以洒脱地修改架构,但在大型数据集上,重新建模几乎是不太可能的。只有当我们的训练结果看起来实在没有明显问题可以调整的时候,我们才会选择重建架构。
- 2、调整参数可以依赖于现在已经训练过的结果继续进行,因此成本较小。但缺点是,参数调整必须依赖于模型有明显问题可以“对症下药”,否则乱调参数无端消耗时间。
对SVHN数据集而言,现在的架构中规中矩——我们适当地使用了数据增强,使用了提前停止,并且测试集上的准确率也趋于平稳,因此架构现在并没有特别突出的问题。但如果可能的话,我们还是希望模型能够尽量地再平稳一些,同时如果可能地话,在后续迭代中控制住过拟合。模型不稳定、模型过拟合是一般迭代过程中最常见的两个问题。我们接下来就基于SVHN数据集来说明调整模型的方式。
6.2 让迭代更稳定
对许多模型来说,除了准确率不够高,最核心的问题就是测试集上的结果不太稳定。如果能够让测试集的结果更稳定,说不定模型还有继续增加迭代次数的可能。为什么模型会不稳定呢?通常可能存在的理由有以下几个:
- 1)数据增强随机性太大、或者bs太小
如果在一个数据集中,我们发现训练集的准确率稳定上升、测试集准确率却在反复横跳(这种反复横跳类似于SVHN数据集训练前期测试集的情况),这说明训练数据中epochs与epochs之间差异太大,并且训练数据与测试数据差距也很大,这会导致模型在优化过程中随机性太强。这可能是因为数据集本身样本与样本之间就差异巨大,而batch_size对于现在的数据集来说太小,也有可能是我们为了防止过拟合而加上的数据增强导致的。
如果可能的话,你可以增加batch_size,如果在现有显存下,很难再增加batch_size,你可以将数据增强取消,或者削弱数据增强中随机的程度,使用更接近原始训练集的数据进行训练,可以提升测试集数据与训练集数据统计上的相似性,从而提升模型效果。当然,取消数据增强很可能降低训练集的学习难度,在已经训练了20+epochs的模型上,取消数据增强有可能直接将模型快速导向过拟合的方向。另外,如果你的训练集上的准确率也在反复横跳,这可能说明模型的学习能力存在问题。先尝试调整batch_size、数据增强等随机的部分看看是否起效,如果不起效,则认真考虑更换架构。
- 2)初始学习率太大,或迭代不稳定
随着训练次数的增多,测试集上的准确率也变得相对稳定,这可能说明模型的起始学习率太大,最开始的时候模型完全是在损失函数上“横冲直撞”找不到方向。为解决这个问题,我们可以降低学习率lr或增加动量参数gamma,来帮助模型稳住迭代方向。如果我们使用的是Adam作为优化算法,则可以考虑增加β值。
- 3)模型的置信度低
对于分类模型,神经网络的预测结果都是softmax或sigmoid函数输出的概率值。一般来说我们依赖于阈值或概率之间的相对大小对具体的类别进行判断,但概率的大小实际上也代表着模型对于自己做出的预测的自信程度(也称之为置信度)。例如,对于阈值为0.5的二分类算法而言,样本A输出的概率值为0.51,样本B的概率值输出为0.9,对着两个样本,模型都会指向预测标签1,但是模型明显更有信心将样本B分类正确。当训练数据发生变化、模型的权重被迭代时,样本上的概率都会发生小范围变化,样本B的概率很可能依然围绕在0.9附近,但样本A的概率很可能在0.45~0.55之间摇摆,这个摇摆很可能会改变样本A的预测结果。如果一个模型对大部分样本的置信度都较低,当模型迭代时,就会存在大量不断变化预测值的样本,这些样本就会导致模型结果剧烈波动。这种情况下,说明模型或架构的学习能力不足,需要更换架构、或通过特征工程降低数据的学习难度、或增强架构的学习能力。
现在我们来尝试一下前两个手段。在训练中,我们已经通过torch.save的代码保存了测试集上准确率最高的一组权重,虽然基于各类随机性,这组权重不一定能够重现出最高的准确率,但我们认为测试准确率是一定程度上代表了模型的泛化能力的。现在我们就基于这组权重来继续训练。
#首先加载之前保存的权重
torch.manual_seed(1412)
resnet18_ = m.resnet18()
net = MyResNet()
net.load_state_dict(torch.load("/Users/zhucan/Desktop/ModelSelection/myResNet_test2.pt"))
加载完成后,会有如下的信息显示:

#修改modelname,准备好保存结果
modelname = "MyResNet_stable5"
#控制变量:每次只调整一个参数
#先调整可能对整个学习过程影响最大的参数:学习率
print(modelname)
torch.manual_seed(1412)
start = time() #计算训练时间
#降低学习率,原本的lr=0.001,现在我尝试了0.0075,0.0005,0.00025和0.0002和0.0001五种
trainloss, testloss = full_procedure(net,epochs=30, bs=256
,modelname=modelname
,PATH = PATH
,lr = 0.0001
,gamma=0
,tol = 10**(-10))
print(time()-start)
plotloss(trainloss,testloss)
得到如下的结果:
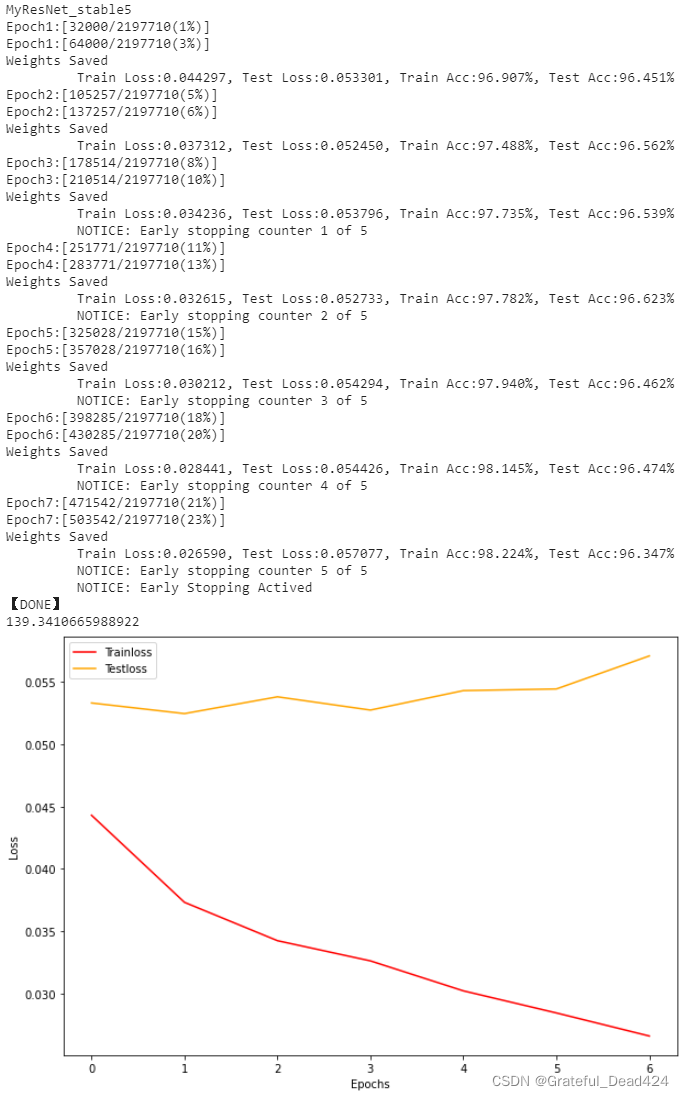
可以看到,将学习率调整为原来的1/10后,模型变得平稳很多,着说明最初设置的学习率0.001对于SVHN数据集来说可能有些过大了。不过,先使用大学习率找到快速到达局部最小值的附近,再使用较小的学习率找到局部最小值,是一种常见的策略。现在,学习率的缩小不仅让模型变得非常平稳,并且提升了模型在测试集上的表现。但可以看到,随着迭代次数的增加,模型是逐渐走向过拟合的。在此基础上,如果将数据增强去除,过拟合会越来越严重。
现在,在模型已经比较平稳的情况下,我们再试试看参数gamma,一个较小的gamma可以帮助参数变得更加平稳。
#在lr稳定的基础上调节gamma
torch.manual_seed(1412)
resnet18_ = m.resnet18()
net.load_state_dict(torch.load("/Users/zhucan/Desktop/ModelSelection/MyResNet_stable5.pt"))
modelname = "MyResNet_stable6"
print(modelname)
start = time() #计算训练时间
net = net.to(device,non_blocking=True)
#基于lr非常小的考虑,同样尝试了非常小的值
trainloss, testloss = full_procedure(net,epochs=30, bs=256
,modelname=modelname
,PATH = PATH
,lr = 0.0001
,gamma = 0.0001
,tol = 10**(-10)
)
print(time()-start)
plotloss(trainloss,testloss)
现在模型已经非常平稳了,从数据的状态来看较小的gamma和小学习率的结合能够让模型非常平稳。不过,模型明显陷入了过拟合的状况,两次训练中训练集都平稳下降,测试集呈现走高趋势。由于我们已经使用了数据增强,因此在这种情况下,我们可以尝试除了数据增强之外的其他对抗过拟合的方法,说不定能够再一次提升测试集上的准确率。
6.3 对抗过拟合
如果模型出现过拟合的情况,则说明至少模型在训练集的学习上并不存在问题,因此我们可以尝试各种控制过拟合的方法来试图削减训练集上的准确率、并提升测试集上的准确率(注意:如果能够成功消除过拟合,基本都是训练集准确率下降、测试集准确率上升的情况)。通常来说,我们控制过拟合的方式有以下几种:
- 1)L1\L2正则化,或权重衰减
也就是在损失函数后加上权重的L1或L2范数表达式,让迭代的时候损失函数因正则项的存在而偏移,从而阻止架构“精确”地学习数据。在优化算法中,我们可以通过参数weight_decay调整权重衰减值。这个值非常敏感,因此调节难度极大,但我们还是可以尝试这么做。
- 2)Dropout/BN
Dropout和Batch Normalization可以控制正则化,其中Dropout多被用于含有全连接层的卷积网络,而BN基本被用于Inception及之后诞生的所有卷积网络。
- 3)降低batch_size/数据增强,增加数据与数据之间的不相似性
这一点正好与迭代不稳定的情况相反。如果出现过拟合,则说明我们需要增加训练数据的随机性来阻止算法对数据的学习。降低batch_size也是同理,通过将每次训练时的批次分得更小,可以有效提升每次训练时样本数据呈现出不同规律和分布的概率。
- 4)降低模型的复杂度
过拟合可能发生的原因之一是在简单数据上使用了过于复杂的架构。当模型复杂度很高、参数很多时,简单数据就很容易被模型“过度学习”,从而导致过拟合。如果存在这样的情况,我们可以削减模型的层、让卷积网络输出的特征图数量变少、让全连接层上输出的值变少,以此降低模型的参数量和复杂度。这个方法需要修改架构,因此当训练流程已经非常深入时,我们一般不会考虑这个方法。
- 5)使用提前停止Early Stopping
提前停止可以在模型刚开始出现过拟合的现象时就停止训练,而我们现在所使用的架构上迭代的结果也说明我们确实在比较恰当的地方实现了提前停止。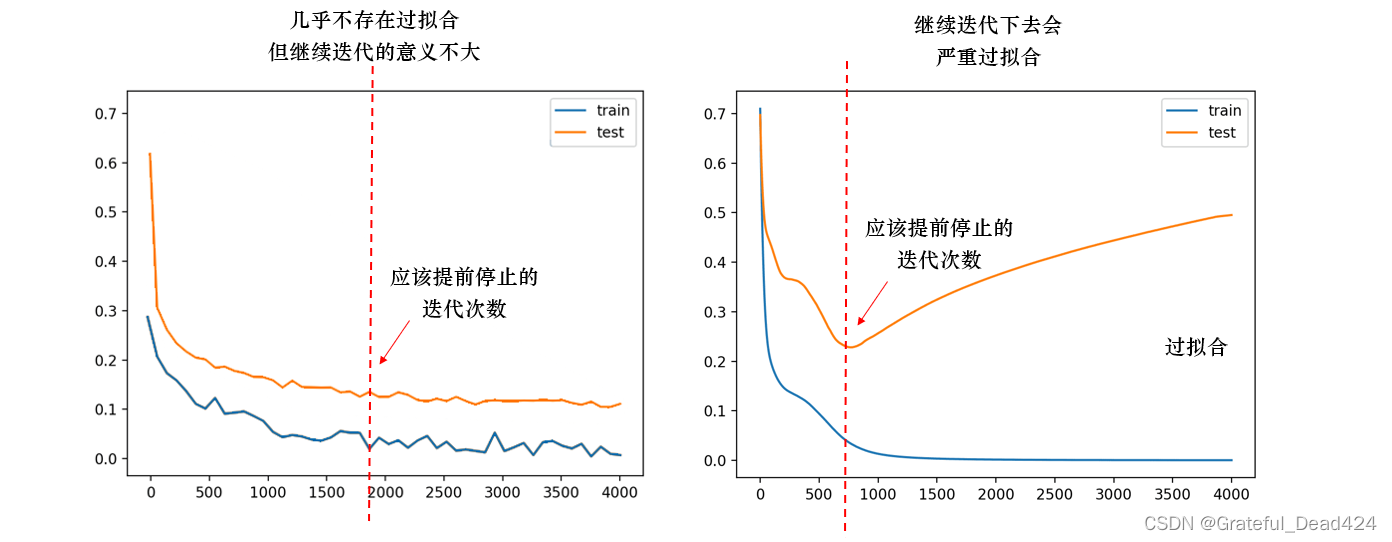
如果上面5种手段你都已经尝试过,但你的模型还是处于过拟合的状态,那你可能需要剑走偏锋了:
- 6)检查你是否使用了不恰当的数据处理过程方式、或参数初始化过程、或预训练过程
比如说,你训练集和测试集上使用的归一化参数不同,或者在过拟合的情况下使用了加速迭代的Xavier初始化、或者使用完全与训练数据不相关的预训练流程等,这些都可能导致模型从训练集上学到的内容和测试集完全不同。同时,还有可能是我们忽视了测试集中的一些奇特的样本,导致模型缺乏足够的“不变性”,这种情况下我们可以再次探索数据,更换数据增强的方式。
对SVHN现在的架构而言,我们在最初就已经使用了2)、5)两种防止过拟合的方法,并且我们也使用了数据增强,还出于让模型迭代更稳定的目的撤销了数据增强。现在我们可以尝试增加权重衰减参数,并且降低batch_size进行训练。我们来尝试一下:
modelname = "MyResNet_overfit"
torch.manual_seed(1412)
resnet18_ = m.resnet18()
net = MyResNet()
net.load_state_dict(torch.load("/Users/zhucan/Desktop/ModelSelection/MyResNet_stable6.pt"))
#在stable6的基础上继续训练
print(modelname)
torch.manual_seed(1412)
net = net.to(device,non_blocking=True)
start = time() #计算训练时间
trainloss, testloss = full_procedure(net,epochs=30, bs=128 #令batch_size下降一半
,modelname=modelname
,PATH = PATH
,lr = 0.0001
,gamma= 0.0001
,tol = 10**(-10)
,wd = 0.00005) #wd非常敏感,因此要小心地进行调整
print(time()-start)
plotloss(trainloss,testloss)
来看下面的结果:
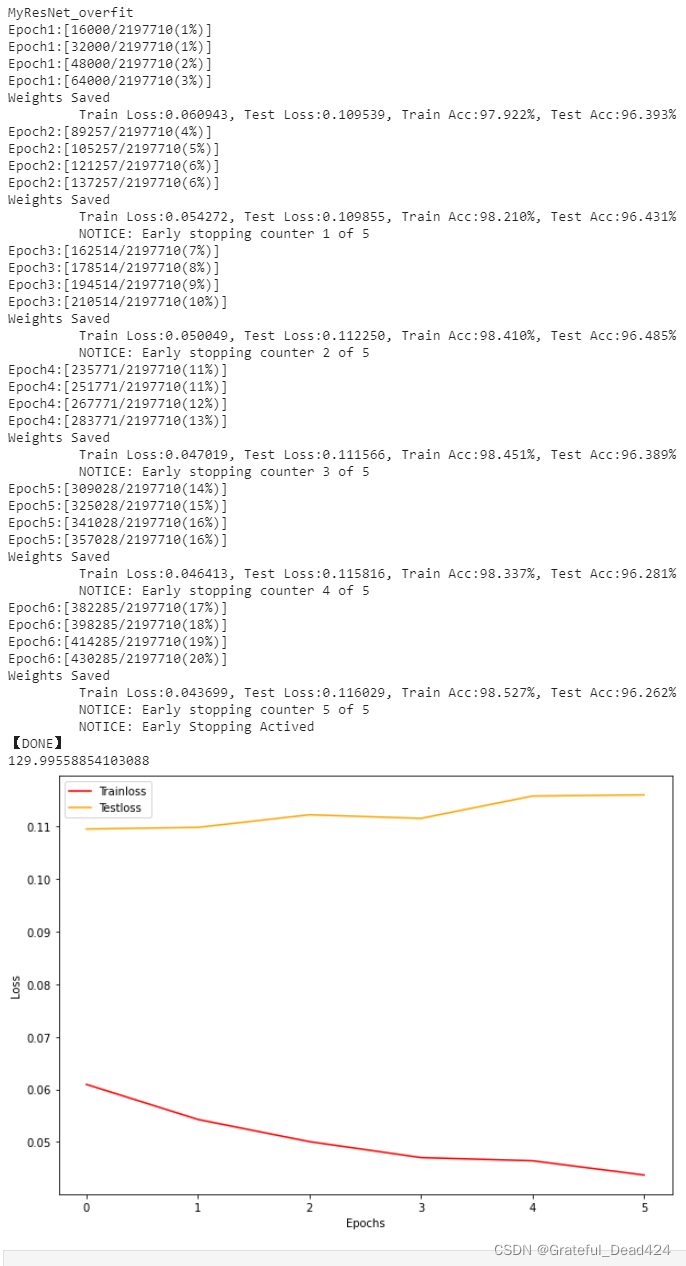
很明显,模型的过拟合进程并没有停止,随着迭代的加深,我们依然在向着过拟合的方向进发。这很可能说明模型已经突破了应该提前停止的界限,现在进行再进行过拟合调节的作用已经不大了。这种情况下,我们可以从0开始迭代,重新寻找应该提前停止的位置。
6.4 基于新参数训练
在这次迭代中,我们先设置0.001作为初次学习的学习率,允许迭代大约15个左右的epochs,然后再使用0.00001这个更小的学习率继续迭代。
#先按大lr进行初期迭代,再按小lr进行后期迭代
PATH = r"D:\Pythonwork\DEEP LEARNING\WEEK 9\models\ConfirmedResNet"
modelname = "myResNet_test0_1"
print(modelname)
torch.manual_seed(1412)
resnet18_ = m.resnet18()
net = MyResNet().to(device,non_blocking=True) #完全重启,不借用任何过去训练好的参数
start = time() #计算训练时间
trainloss, testloss = full_procedure(net,epochs=15, bs=256
,modelname=modelname
,PATH = PATH
,lr=0.001
,tol = 10**(-10)
)
print(time()-start)
plotloss(trainloss,testloss)
结果如下所示:

模型依然极度不稳定,但是也将测试集上的损失迭代到了0.1以下。我们保存了测试集上预测准确率最高的一组参数,接下来就依赖于这组参数继续进行迭代:
modelname = "MyResNet_retrain"
torch.manual_seed(1412)
resnet18_ = m.resnet18()
net.load_state_dict(torch.load("D:\Pythonwork\DEEP LEARNING\WEEK 9\models\ConfirmedResNet\myResNet_test0_1.pt"))
print(modelname)
torch.manual_seed(1412)
net = net.to(device,non_blocking=True)
start = time() #计算训练时间
trainloss, testloss = full_procedure(net,epochs=30, bs=128 #令batch_size下降一半
,modelname=modelname
,PATH = PATH
,lr = 0.00001
,gamma= 0.0001
,tol = 10**(-10)
,wd = 0.00005) #wd非常敏感,因此要小心地进行调整
print(time()-start)
plotloss(trainloss,testloss)
得到的结果如下:
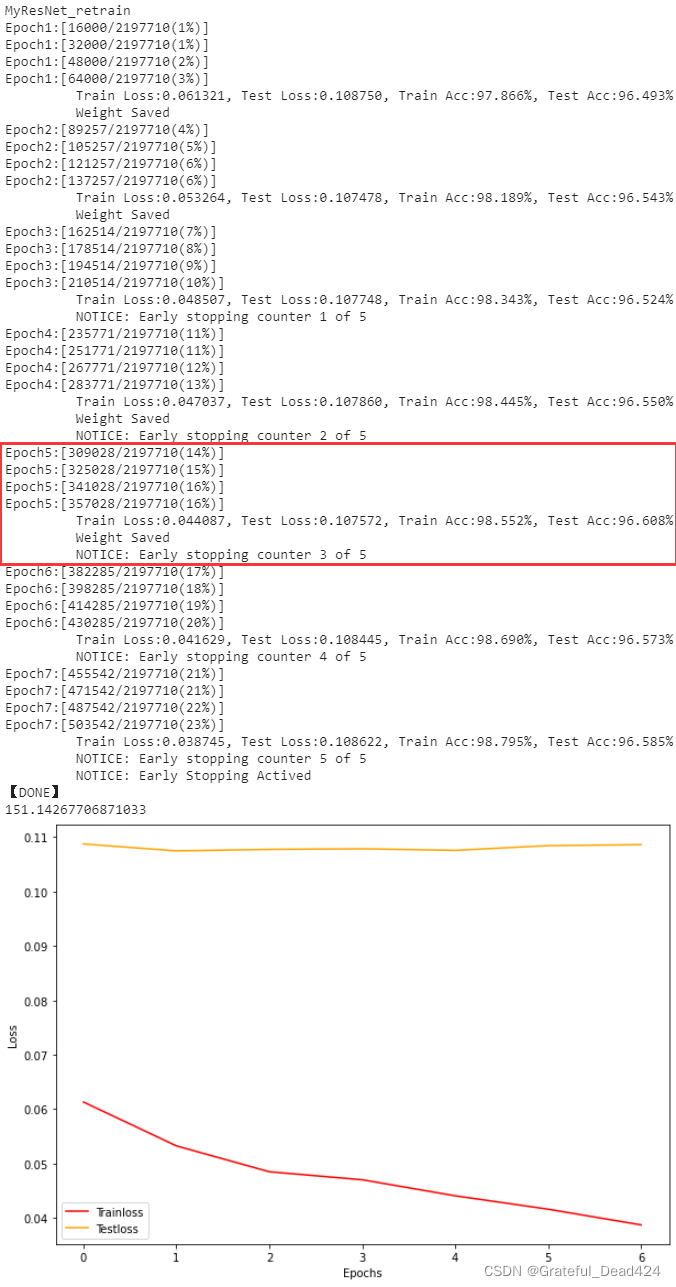
最终,我们得到了稳定在96%以上的模型,并且最高准确率为96.608%,这对于SVHN来说是一个还不错的结果,但还有更多可以调整的方向。很遗憾在有限的时间内我无法在课程中呈现所有的方法,但我可以抛砖引玉,为大家提供更多进阶的路径。
6.5 架构升级,其他可探索的方向
现在我们得到了测试集准确率在96.608%的架构,这是个不错的数字,但依然远远低于我们在训练集上可以达到的99.9%,模型现在依然处于轻度过拟合的状态。轻度过拟合说明现在使用的架构没有提取出能够令测试集做出更准确判断的特征,模型的学习能力或许已经满足了训练集,但是低于测试集的要求,因此我们现在需要再次更改模型架构,提升参数量、并提升模型的复杂度。
先来看现在的架构。我们现在使用了总共9个卷积层、1个输出全连接层,其中8个卷积层都在残差单元中,输出特征图数目分别是128,128,128,256,256,256,256,256。对于SVHN数据集来说,我们很难在现有的架构中继续增加特征图的数目,但增加层也会有所困难,因为SVHN的尺寸决定了我们通常来说只能有2个步长为2的卷积层,除非自己重新写架构,否则想要在成熟的残差网络架构中插入更多的卷积层并不是容易的事儿。
在现有知识范围和架构下,我们是否能够将网络效果提升到更高层次呢?答案是可以,不过要使用一些非常规的手段。对于数字识别数据来说,图像中所含有的信息本身并不多,但是我们确实需要更多的层来加深对信息的提取,或许我们可以让最终输出的特征图变得更小,例如,尝试在7x7大小的特征图后继续增加卷积层或残差单元,让最终输出的特征图尺寸变小为4x4。我们来看看这种操作:
class MyResNet2(nn.Module):
def __init__(self):
super().__init__()
self.block1 = nn.Sequential(nn.Conv2d(3,64,kernel_size=3,stride=1,padding=1,bias=False)
,resnet18_.bn1
,resnet18_.relu)
self.block2 = resnet18_.layer2
self.block3 = resnet18_.layer3
self.block4 = resnet18_.layer4 #其他地方都不变,但增加原始残差网络中的layer4
self.avgpool = resnet18_.avgpool
self.fc = nn.Linear(in_features=512, out_features=10, bias=True)
def forward(self,x):
x = self.block1(x)
x = self.block2(x)
x = self.block3(x)
x = self.block4(x)
x = self.avgpool(x)
x = x.view(x.shape[0],512) #512个输出
x = self.fc(x)
return x
torch.manual_seed(1412)
resnet18_ = m.resnet18()
net2 = MyResNet2()
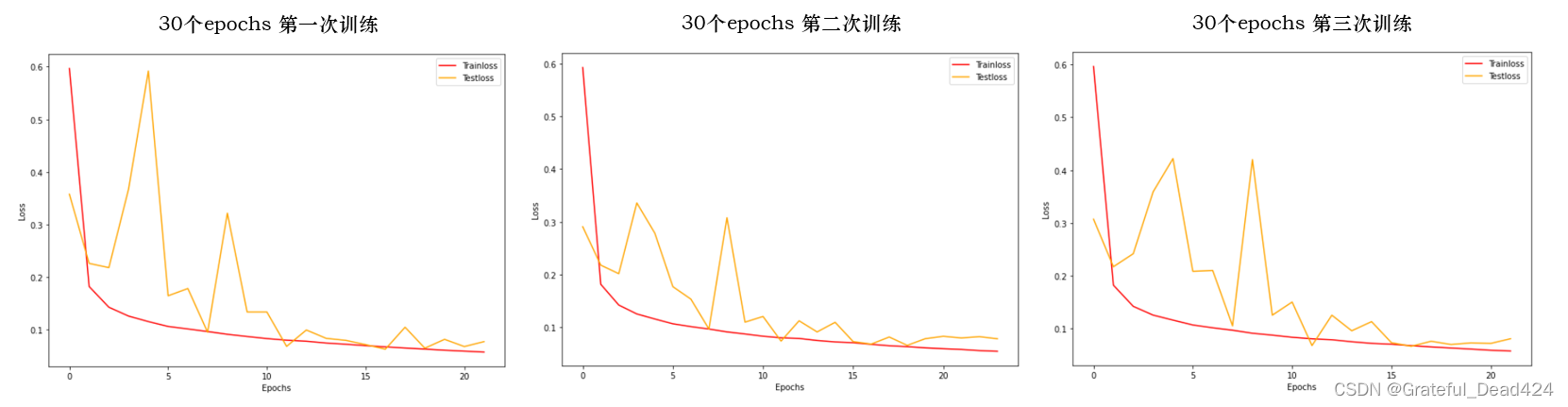
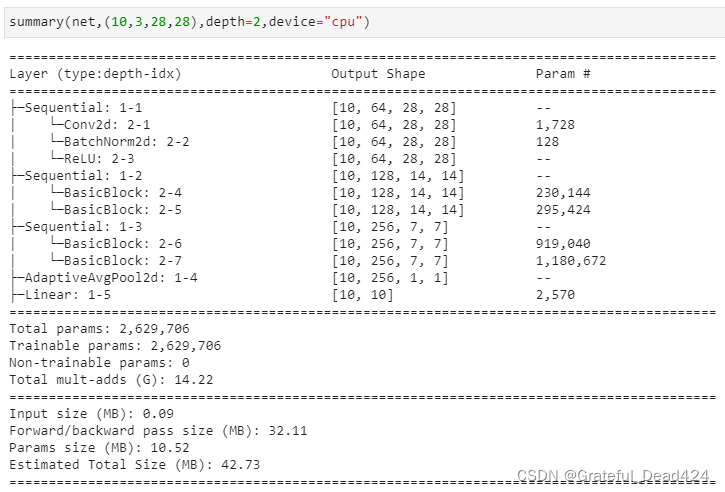
summary(net2,(10,3,28,28),depth=2,device="cpu")
这个操作会让网络中的卷积层增加到13个,让最终输出的特征图数量达到512个,模型总参数会因此进入千万级别。
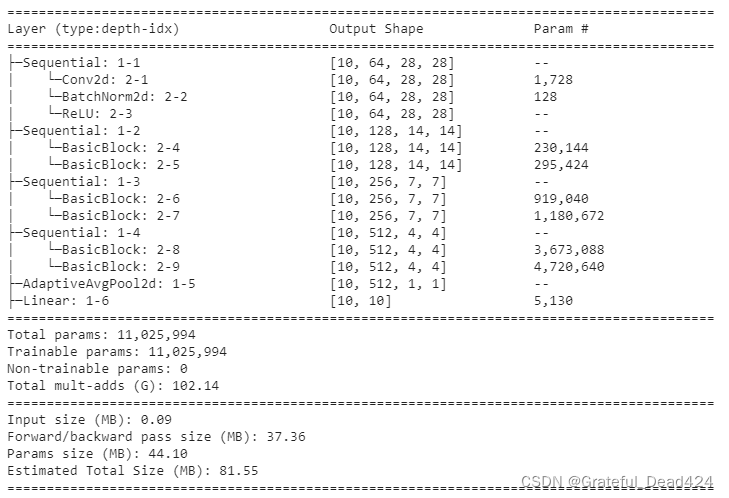
让我们在没有数据增强和有数据增强的情况下分别尝试这个新架构:
'''
===========TIME WARNING==========
===========运行时间警告===========
CPU:Intel i5-10600 @4.10Ghz
GPU:RTX 2060S GPU
MyResNet
1 epoch on CPU: 9min50s~10mins
1 epoch on GPU: 18s~20s
===========运行时间警告============
===========TIME WARNING===========
'''
#没有数据增强,回归原始参数
modelname = "MyResNet2_test1"
print(modelname)
torch.manual_seed(1412)
resnet18_ = m.resnet18()
net2 = MyResNet2().to(device,non_blocking=True)
start = time() #计算训练时间
trainloss, testloss = full_procedure(net2,epochs=30, bs=256
,modelname=modelname
,PATH = PATH
,tol = 10**(-10))
print(time()-start)
plotloss(trainloss,testloss)
结果如下所示:

 首先,训练集上的结果看起来和原来的架构差不多,测试集开始出现一些高分,但同时也变得极度不稳定。为了修正不稳定的问题,我们将使用之前《6.2 让迭代更稳定》中没有生效的、缩小学习率的方式:
首先,训练集上的结果看起来和原来的架构差不多,测试集开始出现一些高分,但同时也变得极度不稳定。为了修正不稳定的问题,我们将使用之前《6.2 让迭代更稳定》中没有生效的、缩小学习率的方式:
modelname = "MyResNet2_test2"
start = time() #计算训练时间
trainloss, testloss = full_procedure(net2,epochs=30, bs=256
,modelname=modelname
,PATH = PATH
,tol = 10**(-10)
,lr = 0.0001)
print(time()-start)
plotloss(trainloss,testloss)
来看稳定性和模型结果的变化:
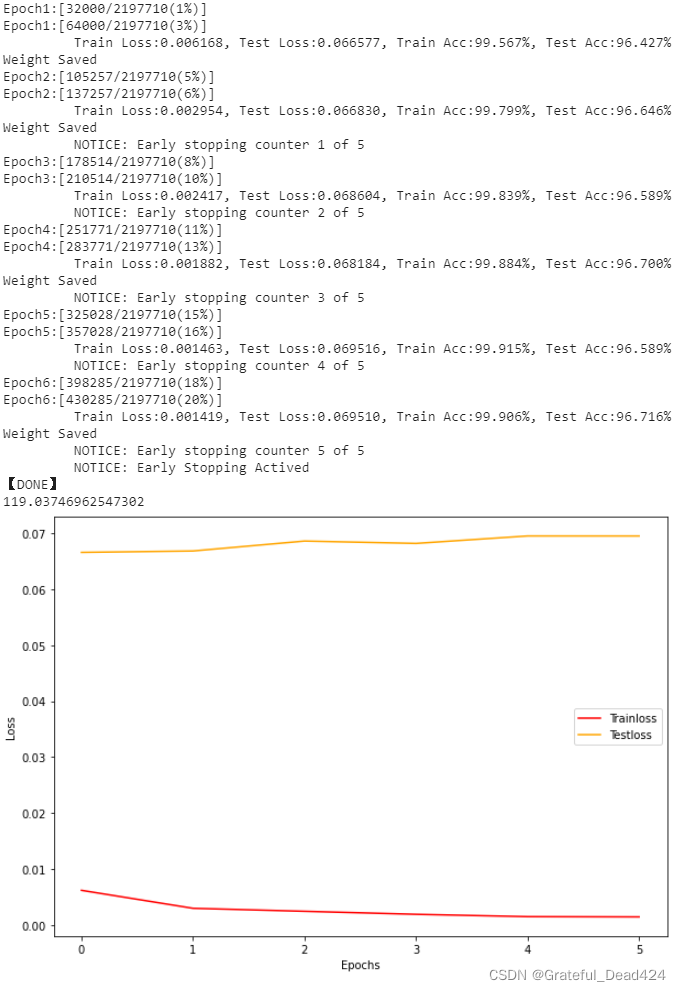
你会发现,没有经过太多参数的尝试和调整,我们的架构轻易地超过了96.608%这个准确率,得到了96.716%的准确率。在有足够算力的前提下,如果能在新架构上继续训练,想必能够将模型准确率提高至97%以上。我们通过强行加深网络、将特征图最终的尺寸修改为4x4提升了模型效果,可以看出SVHN数据集上的信息的确需要更深的神经网络来进行学习。然而,这种更改模型架构的方式毕竟还是剑走偏锋,并不能轻易推广到其他数据集或其他架构上。如果我们希望继续提升模型的效果,我建议以下的几种手段,操作难度逐渐递增:
- 1、尝试使用预处理、各类初始化等手段,看看能否继续优化网络
- 2、深入研究标签类别中,究竟哪些数字不容易被判断正确,针对这些数字或图像做特定的数据增强
- 3、学习论文中提到的各种手段和新兴模型,在新兴模型上尝试SVHN数据集的结果
基本上来说,能够在SVHN数据集上稳定输出更高结果(超过97%)的架构都借用了更高级的数据处理手段、初始化手段、迭代方式或者更强大的模型(像我们这样硬生生跑到接近97%的估计很少)。其中,影响数据和迭代的技术包括Maxout正则化、梯度池化、DropConnect、AutoAugment、Cutout等,更强大的模型则包括了密集链接的卷积网络(DCNN,也叫作DenseNet)、多层残差网络(Multilevel ResNet)、宽残差网络(WRN)等等。如果我们希望提升模型的效果,这些论文都可以作为参考。 - 4、获取最原始的数据集,重新创造图像尺寸更大的数据集,帮助我们加深网络
SVHN数据集的数字图像是经过SVHN创作团队处理后,可以被用于简单分类的图像。但SVHN数据集的原始图像是谷歌地球上街景实拍图,这些实拍图是开放下载的。我们可以找到实拍图后,重新对实拍图进行描框、生成尺寸更大的数据集(例如3x64x64),这样我们就可以更自由地使用更深的网络对SVHN数据集进行训练了。在此基础上,如果你还有更多手段和方法,欢迎随时在群里进行分享。
