[人工智能]图像金字塔、高斯金字塔、拉普拉斯金字塔是怎么回事？附利用拉普拉斯金字塔和高斯金字塔重构原图的Python-OpenCV代码

图像金字塔是通过多个分辨率表示图像的一种有效且简单的结构。
一个图像金字塔是一系列以金字塔形状排列的分辨率逐步降低的图像。图像金字塔的底部是待处理图像的高分辨率表示，而顶部是低分辨率表示。

图像金字塔有什么作用？
图像金字塔常用于图像缩放、图像重构、图像融合、图像增强技术中。
这里说下图像金字塔在图像融合技术中的应用。多分辨率塔式图像融合算法是现在较为常用的图像融合方法。在这类算法中，原图像被层层滤波和缩小，形成一个塔状结构。在塔的每一层都用一种融合算法对这一层的数据进行融合，从而得到一个经算法处理后的塔式结构，然后对处理后的塔式结构进行重构，从而得到合成图像。
另外，图像金字塔可以将原图像分别分解到不同的空间频带上，这样就可以针对不同分解层的不同频带上的特征与细节，采用不同的算子以达到更有针对性的算法优化处理。

高斯金字塔和拉普拉斯金字塔是最常见的两种图像金字塔。

下面详细介绍高斯金字塔和拉普拉斯金字塔。

先说高斯金字塔。
高斯金字塔是指通过高斯模糊滤波和下采样不断地将图像的尺寸缩小，进而在金字塔中包含多个分辨率的一组图像。高斯金字塔的形式如下图所示：

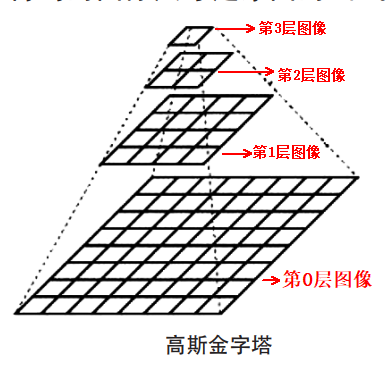
一般情况下，高斯金字塔的最底层为原图像，每向上一层就会通过高斯模糊滤波+下采样缩小一次图像的尺寸。
通常情况下，图像的长与宽会缩小为原来的一半，由于每次图像的长与宽都缩小为原来的一半，图像的缩小速度非常快，因此常见的高斯金字塔的层数为3~6。

在OpenCV中提供了函数pyrDown()，用于生成图像的上一层高斯金字塔。
函数pyrDown()的原型如下：

void cv::pyrDown(	InputArray 	src,
					OutputArray 	dst,
					const Size & 	dstsize = Size(),
					int 	borderType = BORDER_DEFAULT 
				)	

下面介绍下这个函数的参数：
src—输入图像
dst—输出图像，它的宽度和高度大致为src的1/2 ，具体精确的大小由第三个参数dstsize决定。
dstsize—目标图像的大小，默认值为Size((src.cols+1)/2, (src.rows+1)/2)，自己指定时需要满足以下条件。

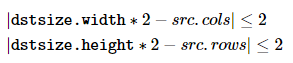
bordertype—做高斯卷各时的边界外推标志。详情见下面这篇博文：
https://blog.csdn.net/wenhao_ir/article/details/124177989
使数函数pyrDown()生成上一层高斯金字塔包含两个过程，即高斯核卷积和下采样两个过程。
设$G_n$表示第n层高斯金字塔的图像，则$G_0$表示高斯金字塔的最底层，这一层实际上就是原图像。为了得到$G_{n+1}$，首先需要对$G_n$进行高斯核卷积，即做高斯低通滤波，然后删除所有的偶数行和偶数列(这是一种下采样操作)，从而得到$G_{n+1}$。这个函数使用的高斯核如下：

提问：为什么高斯金字塔在下采样操作之前要先进行高斯低通滤波。
答：这样做既是保证高斯金字塔低通处理的性质，又能对图像进行平滑，使图像不至于出现边界缝隙。
总结一下：图像高斯金字塔的上一层是对下一层进行低通滤波后再进行隔行隔列采样得到的。上一层图像的大小约为下一层图像的1/4。

高斯金字塔说得差不多了，接下来说拉普拉斯金字塔。
拉普拉斯金字塔实际上是作为高斯金字塔的图像重建而存在的。它是由高斯金字塔生成的。拉普拉斯金字塔是高斯金字塔与其上一层通过上采样扩大后的差值图像，这里的上采样一般采用插值的方式进行。这句话有点拗口，可以看下面这幅图帮助理解拉普拉斯金字塔是怎么回事。

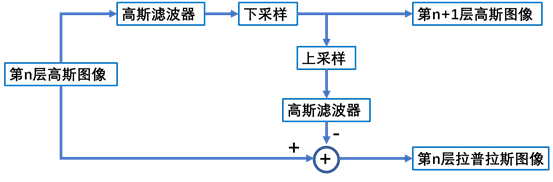
从上面的叙述，再结合高斯滤波器是一种低通滤波器，所以我们可以说某一级的拉普拉斯金字塔可以反映出其同级的高斯金字塔的高频分量。有些文献把拉普拉斯金字塔反映其同级高斯金字塔的高频分量的性质称为拉普拉斯金字塔的预测残差作用。

从上面拉普拉斯金字塔的生成过程我们可以看出，在利用高斯金字塔生成拉普拉斯金字塔的过程中，假设高斯金字塔为N层，则在计算第N层的拉普拉斯金字塔时我们还要额外计算出第N+1层的高斯金字塔才能进而计算出第N层的拉普拉斯金字塔。

OpenCV提供了函数pyrUp()用于帮助计算出拉普拉斯金字塔。通过它可以把第n层的高斯金字塔图像进行上采样后再进行高斯卷积模糊滤波操作。
OpenCV官方文档中对其功能的描述如下：
“The function performs the upsampling step of the Gaussian pyramid construction, though it can actually be used to construct the Laplacian pyramid. First, it upsamples the source image by injecting even zero rows and columns and then convolves the result with the same kernel as in pyrDown multiplied by 4”
从上面的描述中我们可知，函数pyrUp()的上采样操作是均匀地隔行隔列加0值。上采样完成之后用下面这个卷积核进行高斯卷积模糊滤波操作。

请注意：上面这个卷积核与函数pyrDown()的卷积核有所不同，具体是函数pyrDown()高斯卷积核需要乘以四才得到函数pyrUp()的卷积核，至于为什么要这样做，博主目前没有搞清楚。猜想应该是与其上采样的插值方式有关吧。知道原因的朋友请在这篇博文下留言交流吧。

它的原型如下：

void cv::pyrUp	(	InputArray 	src,
					OutputArray 	dst,
					const Size & 	dstsize = Size(),
					int 	borderType = BORDER_DEFAULT 
				)	

各参数的意义和函数pyrDown()的一样，这里就不再赘述了。

这里要特别注意：函数pyrDown()的dst参数中得到的并不是拉普拉斯金字塔图像。
如果要得到拉普拉斯金字塔图像，还需要按下面的公式进行运算。
令$L_n$表示第n层拉普拉斯金字塔，$G_n$表示第n层高斯金字塔，则有：

$L_n=G_n?Pyrup(Pyrdown(G_n))$

显然我们可以利用下面的公式重构第n层高斯金字塔图像：
$G_n^{{}^{\prime }}=L_n+Pyrup(G_{n+1})$

接下来上基于Python-OpenCV的示例代码：
代码中用到的图像下载链接如下：
链接：https://pan.baidu.com/s/1xj_4ZS70XHZ8klqdgAXPrA 提取码：2abg

# 博主微信/QQ 2487872782
# 有问题可以联系博主交流
# 有图像处理需求也可联系博主
# 图像处理技术交流QQ群 271891601

# !/usr/bin/env python
# -*- coding: utf-8 -*-
# OpenCV的版本为4.1

import cv2 as cv

src = cv.imread("F:/material/images/P0036-view-256_256.jpg")

G_0 = src  # 第0层高斯金字塔实际上就是原图像
print('第0层高斯金字塔图像的尺寸：{}'.format(src.shape[:2]))
cv.imshow("G_0", src)

# 生成第1层高斯金字塔G_1
G_1 = cv.pyrDown(G_0)
print('第1层高斯金字塔图像的尺寸：{}'.format(G_1.shape[:2]))
cv.imshow("G_1 ", G_1)

# 为了计算第0层拉普拉斯金字塔，我们需要先计算出Pyrup(G_1)
Pyrup_G_1 = cv.pyrUp(G_1)
print('第1层高斯金字塔进行上采样+高斯卷积模糊滤波后的尺寸：{}'.format(Pyrup_G_1.shape[:2]))
cv.imshow("Pyrup_G_1", Pyrup_G_1)

# 计算第0层拉普拉斯金字塔图像，L_0=G_0-Pyrup(Pyrdown(G_0))
L_0 = cv.subtract(G_0, Pyrup_G_1, dst=None, mask=None, dtype=cv.CV_16S)
print('第0层拉普拉斯金字塔的尺寸：{}'.format(L_0.shape[:2]))

# 以下几行代码是显示出第0层拉普拉斯金字塔的图像
L_0_norm = L_0
cv.normalize(L_0, L_0_norm, 0, 255, cv.NORM_MINMAX)
L_0_norm = L_0_norm.astype('uint8')
L_0_norm_gray = cv.cvtColor(L_0_norm, cv.COLOR_BGR2GRAY)
cv.imshow("L_0_norm_gray", L_0_norm_gray)

# 利用第1层高斯金字塔图像和第0层拉普拉斯金字塔图像重构第0层高斯金字塔
# 第0层高斯金字塔实际上就是原图
G_0_reconstruction = cv.add(Pyrup_G_1, L_0, dst=None, mask=None, dtype=cv.CV_16S)
cv.normalize(G_0_reconstruction, G_0_reconstruction, 0, 255, cv.NORM_MINMAX)
G_0_reconstruction = G_0_reconstruction.astype('uint8')
print('重构的第0层高斯金字塔图像的尺寸：{}'.format(G_0_reconstruction.shape[:2]))
cv.imshow("G_0_reconstruction", G_0_reconstruction)

cv.waitKey()

运行结果如下图所示：


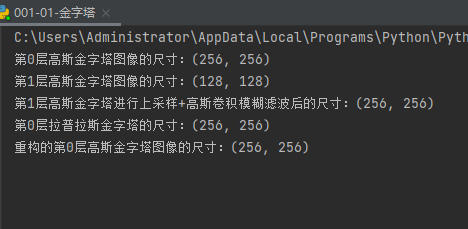
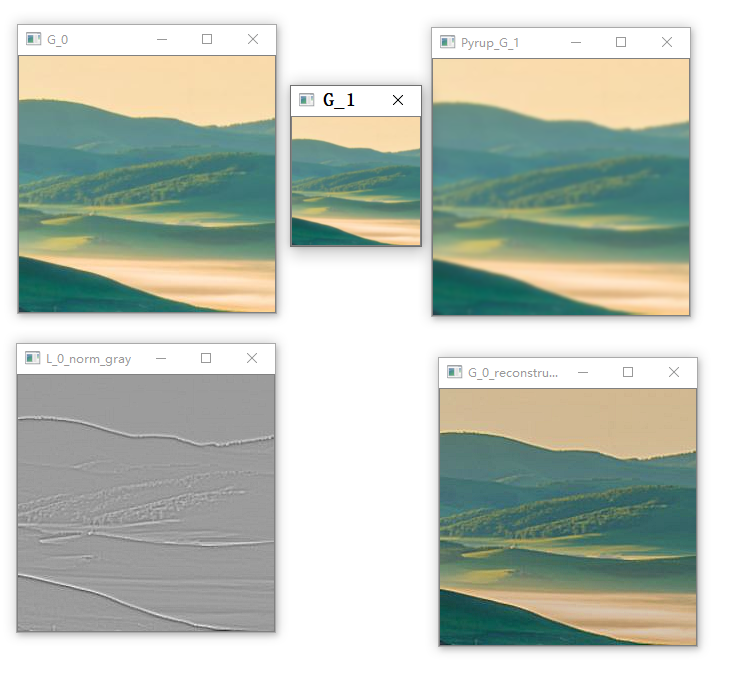
从上面的结果中我们可以看出，利用上一层高斯金字塔和同一层拉普拉斯金字塔重构出的图像在细节上(高频分量上)并没有多少缺失。

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖