[人工智能] 论文阅读《Calculation Method for Visual Navigation Integrity Monitoring》

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 论文阅读《Calculation Method for Visual Navigation Integrity Monitoring》 -> 正文阅读

[人工智能]论文阅读《Calculation Method for Visual Navigation Integrity Monitoring》

摘要

本发明提供一种视觉导航完好性监测的计算方法。该方法利用合适的视觉定位模型、数学算法和丰富的导航测量数据，提高了定位精度和定位结果的可用性。解决了GNSS在复杂环境下无法保证可用性而导致卫星完好性算法性能不足的问题，有助于实现飞机紧密进近和自主着陆，对确保航空飞行安全具有重要意义。

在这里插入图片描述

图1 视觉完好性监测流程图

在这里插入图片描述

图2 人工目标的定位模型

在这里插入图片描述

图3 机场跑道的定位模型

在这里插入图片描述

图4 保护水平计算流程图

交叉参考相关专利申请

略

技术领域

本发明涉及卫星导航技术领域，具体地说，涉及一种用于视觉导航完好性监测的计算方法。

1 背景

随着卫星导航技术的发展和广泛应用，人们越来越认识到全球卫星导航系统完好性的重要性。一份调查报告显示，在航空应用中，致命事故大多发生在最后的进近和降落阶段。尽管飞机的进近和降落阶段虽然最短，但也是保障生命安全最关键的环节。

全球定位系统(GPS)接收机的自主完好性监测通过检查卫星定位观测的一致性来提供导航系统的完好性。然而，在飞行路径的进近和着陆阶段，由于卫星定位观测的不足，现有的接收机自主完好性监测方法的性能一般不能满足严格航空应用对完好性和可用性的要求。因此，开发辅助GNSS的视觉导航设备已成为航空卫星导航领域的一个热点。

目前，北京航空航天大学和西安导航技术研究所等高校和研究机构对卫星导航的完好性进行了理论和技术研究。从GPS到差分GPS，再到其它导航系统，如惯性导航系统和组合导航系统，对卫星导航的完好性进行了越来越多的研究。与此同时，卫星定位完好性监测方法已经相对成熟，但卫星定位信号在所有环境或操作条件下的永久可用性无法得到保证，导致卫星完好性算法的性能不足。因此，本发明提出了一种用于监测视觉辅助导航系统完好性的研究方法。

2 总结

为解决现有技术中由于无法保证复杂环境或操作条件下卫星定位的性能可用性而导致卫星完好性算法性能不足的问题，本发明提供了一种视觉导航完整性监测计算方法。其中包括：

根据具体的视觉定位场景建立合适的视觉定位模型，计算出视觉定位解；
修正视觉系统参数的误差，并计算误差状态向量；
建立视觉观测模型，计算视觉系统观测矩阵 $H$ ；
引入视觉故障偏差，分析故障偏差向量 $b$ 随视觉观测值的变化；
结合视觉系统观测方程和卫星定位方程计算组合导航定位方程；
计算不同故障模式下的保护水平。

步骤(1)中的视觉定位模型在具体的视觉定位场景中可分为两类，第一类为手动设置地标作为着陆参考，第二类为机场跑道作为着陆参考。手动设置的地面标志为“H”或“I”标志；而使用机场跑道作为着陆参考就是借用机场环境附近的机场跑道等高线，这样相机就可以可靠地识别机场跑道目标。进一步，在导航坐标系下构建视觉定位方程如下：
$t_m^n=s_m^n+p^n+q^n$
当路标在相机系下的视线向量 $s_m^c$ 、相机在机体系的位置 $q^b=[x_1\ y_2\ z_3]^T$ 和着陆路标的位置向量 $t_m^n=[x_2\ y_2\ z_2]^T$ 已知时，飞机在三维世界的位置 $p^n=[x_3\ y_3\ z_3]^T$ 可以被计算。其中 $t_m^n$ 表示第 $m$ 个路标点在导航系中的位置向量； $s_m^n$ 表示第 $m$ 个目标在导航系下的视线向量； $p^n$ 表示在导航系下的飞机位置向量； $q^n$ 表示相机中心到飞机质心的距离，它也被称为相机和飞机之间的最小角度偏移向量； $q^b$ 表示机体系中相机的位置，它可以通过相机进行校准。

进一步，对视觉系统参数的误差进行修正，并计算误差状态向量的步骤具体如下：

将基于上述数学参数的误差状态向量表示为：
$\delta x=[\beta p^n \ \delta t_m^n]$
其中 $\delta p^n$ 指飞机三维位置的误差向量： $\delta p^n=\tilde{p}^n-p^n$ ； $\delta t_m^n$ 是路标误差向量： $\delta t_m^n=\tilde{t}_m^n-t_m^n$ ，其中标称值用波浪线表示。
当一个着陆路标进入和离开相机视野时，路标的数量实际上会随着时间而变化，但必须有一个合理的最大路标跟踪数量，以保持计算效率。

进一步，计算视觉系统观测矩阵 $H_{is}$ 的步骤具体如下：

$m g$ 路标视觉观测方程表示为：
$z_m(t_i)=T_c^{pix}\underline{s}_m^c(t_i)+v(t_i)$
其中 $z_m(t_i)$ 是着陆路标点 $m$ 的像素位置； $T_c^{pix}$ 是像素坐标系和相机坐标系之间的变换矩阵； $s_m^c$ 指像素位置对应于从相机焦点向外延伸的视线向量； $s_{m_z}^c$ 是相机在 $s_z$ 方向上到光学中心的距离； $\underline{s}_m^c(t_i)$ 是相机到目标 $m$ 的视线向量的标准化形式； $v(t_i)$ 是一个均值为0协方差为 $R$ 的独立的加性高斯白噪声，它满足以下关系：
$E[v(t_i)v^t(t_j)]=\begin{cases} R, \ \ t_i=t_j \\ 0, \ \ \ t_i \neq t_j \end{cases}$
设在一个高 $H$ 宽 $W$ 的矩形 $(M\times N)$ 像素网格中，像素坐标系与相机坐标系的变换关系为 $T_c^{pix}$ ，它是已知的， $T_c^{pix}$ 和 $T_{pix}^c$ 之间的关系如下：
$T_{pix}^c = \begin{bmatrix} -\frac{H}{fM} & 0 & \frac{H(M+1)}{2fM} \\ 0 & \frac{W}{fN} & -\frac{W(N+1)}{2fN} \\ 0 & 0 & 1 \end{bmatrix} = (T_c^{pix})^{-1}$
一个非线性方程 $z_m(t_i)=T_c^{pix}\underline{s}_m^c(t_i)+v(t_i)$ 被线性化，一个非线性函数被设为 $h[x(t_i)]=T_c^{pix}\underline{s}_m^c(t_i)$ ，计算了一阶泰勒展开式，得到视觉系统观测矩阵 $H$ ，由下式得到的视觉系统观测矩阵 $H$ 中元素的偏导数为：
$H=[\frac{\partial h}{\partial p^n}\ 0]$
因为，
$q^n=C_b^nC_c^bs_m^c+C_b^nq^d=C_b^n(C_c^bs_m^c+q^d)$
$h$ 相对于 $p^n$ 的偏导数为：
$\frac{\partial h}{\partial p^n}=\frac{1}{s_{m_z}^c}T_c^{pix}(\underline{s}_m^cC_n^bC_b^c-C_n^bC_b^c)$
因为视觉系统观测矩阵 $H$ 与 $t_m^n$ 无关， $H$ 对 $\delta t_m^n$ 的偏导数为零。

进一步，分析故障偏差向量 $b$ 对视线观测向量 $z$ 的变化过程如下：

状态向量 $x$ 的线性化视觉观测模型表示为：
$z = H x + v + b$
其中 $z$ 是视觉观测向量；状态向量 $x$ 是 $n$ 维的列向量； $v$ 是一个 $m$ 维的观测噪声向量，服从均值为零的高斯分布，它的协方差矩阵是对角阵 $R$ ，表示为 $R=\sigma^2I_{m*n}$ ； $b$ 是一个 $m$ 维的故障偏差向量，在无故障条件下， $b$ 是一个零向量，当第 $i$ 个测量中出现单故障时， $b$ 中的第 $i$ 个元素仍表示为 $b$ 。
当视觉观测向量变化时，视觉观测误差 $\delta z$ 表示为： $\delta z=H\delta x$ ；因此，得到 $z = H x + v + b$ 的最小二乘解为：
$\delta x=(H^TH)^{-1}H^T\delta z$
如果不考虑噪声向量，则有状态向量 $x$ 的线性观测模型可得：
$\delta x = \hat{x}-x=\bar{H}z=\bar{H}b$
其中 $\bar{H}=(H^TH)^{-1}H^T$
由于故障偏差向量 $b$ 对像素点 $(x, y)$ 的每个分量 $x$ 和 $y$ 都有影响，因此故障偏差向量在极坐标下表示为： $b_i=||b||cos\theta$ 和 $b_j=||b||sin\theta$ ；则 $b_i=||b||cos\theta$ 为故障偏差向量 $b$ 对分量 $x$ 的影响， $b_j=||b||sin\theta$ 为故障偏差向量 $b$ 对分量 $y$ 的影响；因此，位置误差的范数为： $||\delta x||^2=(\bar{H}b)^T\bar{H}b$ ；因为，
$(\bar{H}b)^T\bar{H}b=b^T\bar{H}^T\bar{H}b=b_ib_i(\bar{H}^T\bar{H})_{ii}+b_ib_j(\bar{H}^T\bar{H})_{ij}+b_ib_j(H^TH)_{ji}+b_jb_j(\bar{H}^T\bar{H})_{jj}$
将其代入极坐标公式，可得故障偏差向量 $b$ 对水平位置误差的影响公式为：
$\delta x=\big( ||b||^2(sin2\theta(\bar{H}^T\bar{H})_{ii}+sin2\theta(\bar{H}^T\bar{H})_{ij}+cos^2\theta(\bar{H}^T\bar{H})_{jj}) \big)^{\frac{1}{2}}$
因此，因此，当角度值 $\theta$ 发生变化时，水平位置误差也会发生相应的变化，特别是当对 $\theta$ 取一些特殊的角度值时，水平位置误差 $\delta x$ 的公式可以简化。

进一步介绍了组合导航定位方程的求解过程：

假设卫星定位方程是 $z = G x$ ，结合视觉系统的观测矩阵 $H$ 和卫星的观测矩阵 $G$ 来获得扩展的观测矩阵 $H^{'}$ ，它可以表示为，
$H'=\begin{bmatrix} H \\ G \end{bmatrix}$
$H^{'}$ 是一个 $m\times n$ 的线性观测矩阵。
当一个视觉系统是由两个相机或三个相机组成时，单个相机的变换矩阵 $M_1$ 、 $M_2$ 和 $M_i$ 可以合并成 $M$ ， $M$ 可以表示为：
$M=\begin{bmatrix} M_1 & 0 & 0\\ 0 & M_2 & 0 \\ 0 & 0 & M_i \end{bmatrix}$

进而，将保护水平的计算方法分为三个假设：假设1、假设2和假设3。假设1是在观测中没有故障。假设2是观测中有单个故障。假设3是在观测中存在两个故障。

进而，在假设1的情况下，可以根据无故障放大因子 $K_{ff}$ 和水平位置标准差计算保护水平，其中无故障放大因子 $K_{ff}$ 由无故障概率 $P_{ff}$ 确定。因此，无故障保护水平的计算公式为：
$HPL_1=K_{ff}(k)*\sigma_x$
其中 $K_{ff}$ 是无故障放大因子， $\sigma_x$ 是飞机水平方向的标准差。

在假设2的情况下，单个视觉观测故障或单个卫星观测故障是可能的。当只有一个观测故障时，故障偏差向量 $b$ 中只包含一个偏差分量，现在水平位置误差 $\delta x$ 可以表示为：
$\delta x = \hat{x} - x=\bar{H}z=\bar{H}b$
其中 $\hat{x}$ 表示最小二乘估计值， $H=(H^TH)^{-1}H^T$ 。每个观测的斜率被设置为 $H s l o p e$ ，表示如下：
$Hsolpe_i=\frac{\delta x^2}{D}=\frac{||\delta x||^2}{||p||^2}=\frac{\delta x^T\delta x}{p^Tp}=\frac{b^T\bar{H}^T\bar{H}b}{b^TP^TPb}$
其中 $b^T\bar{H}^T\bar{H}b=b_ib_i(\bar{H}^T\bar{H})_{ii}+b_ib_j(\bar{H}^T\bar{H})_{ij}+b_ib_j(\bar{H}^T\bar{H})_{ji}+b_jb_j(\bar{H}^T\bar{H})_{jj}$ ； $D$ 是统计检验量； $p$ 表示奇偶向量； $P$ 表示奇偶变换矩阵， $p = P b$ 。因此，水平定位误差的保护水平 $HPL_2$ 为：
$HPL_2=Hsolpe_{max}\times s_{bias}$
其中
$s_{bias}=\sigma \frac{\sqrt{\lambda}}{\sqrt{n-4}}$
其中 $\sigma$ 是噪声协方差； $\lambda$ 是分散参数。当无故障时， $HPL_2$ 的值最小；当观测中存在单故障时， $HPL_2$ 的值会增加。

在假设3的情况下，有可能两个视觉观测发生故障，或者两个卫星定位观测发生故障，又或者一个视觉观测发生故障和一个卫星定位观测发生故障。当两个观测发生故障时，第 $i$ 次观测和第 $j$ 次观测同时故障的故障偏差向量为 $b^{(i)}$ 和 $b^{(j)}$ ，可以表示为：
$b=[0\ \cdots \ 0 \ b^{(i)} \ b^{(j)} \ 0 \ \cdots \ 0]^T$
因此，定位误差可以表示如下：
$\Delta = \bar{H}b=Ab=[b^{(i)}A_{1i}+b^{(j)}A_{1j}b^{(i)}A_{2i}+b^{(j)}A_{2i}b^{(i)}A_{3i}+b^{(j)}A_{3i}b^{(i)}A_{4i}+b^{(j)}A_{4j}]^T$
水平定位误差表示如下：
$\delta x^2=(b^{(i)}A_{1i}+b^{(j)}A_{1j})^2+(b^{(i)}A_{2i}+b^{(j)}A_{2j})^2$
因此，斜率计算公式 $H s l o p e$ 为：
$Hslope_i=\frac{\delta x^2}{D}=\frac{||\delta x||^2}{||p||^2}=\frac{\delta x^T\delta x}{p^Tp}=\frac{(b^{(i)}A_{1i}+b^{(j)}A_{1j})^2+(b^{(i)}A_{2i}+b^{(j)}A_{2j})^2}{b^TP^TPb}$
因此，计算 $HPL_3$ 的公式如下：
$HPL_3=Hslope_{max}\times s_{bias}$
将假设1、假设2和假设3结合起来，将所有情况下的误差都包含在保护水平中，得到总保护水平的计算公式如下：
$HPL=\sqrt{max(HPL_1,HPL_2)^2+HPL_3^2}$
进而，第 $m$ 个路标点的视觉测量方程 $z_m(t_i)=T_c^{pix}\underline{s}_m^c(t_i)+v(t_i)$ 也称为伪距离定位方程。

与现有技术相比，本发明具有以下有益效果。本发明提供一种视觉导航完好性监测的计算方法。针对不同的实际情况，提出了合适的视觉定位测量模型和数学算法，丰富了导航观测数据，提高了定位精度和完好性监测性能。解决了现有技术中由于无法保证复杂环境或操作下卫星定位的可用性而导致卫星完好性算法性能不足的缺点。

3 图的简要说明

为了使本发明的内容更容易理解，下面参照本发明的具体实施例及其附图进一步详细地描述本发明。图1是本实例中视觉完好性监测的流程图。图2显示了本实例中人工目标的定位模型。图3显示了本实例中机场跑道的定位模型。图4是本实例中保护水平计算的流程图。

4 详细描述

本发明的目标和功能以及用于实现这些目标和功能的方法将参照实例加以阐明。然而，本发明不限于以下所公开的实例。它可以以不同的形式实施。本说明书的本质仅仅是帮助该领域的技术人员全面地理解本发明的具体细节。

下面将参照附图描述本发明的实例。在图纸中，相同的参考数字代表相同或相似的部分，或相同或相似的步骤。下面通过具体实例描述了一种根据本发明的视觉导航完好性监测的计算方法。

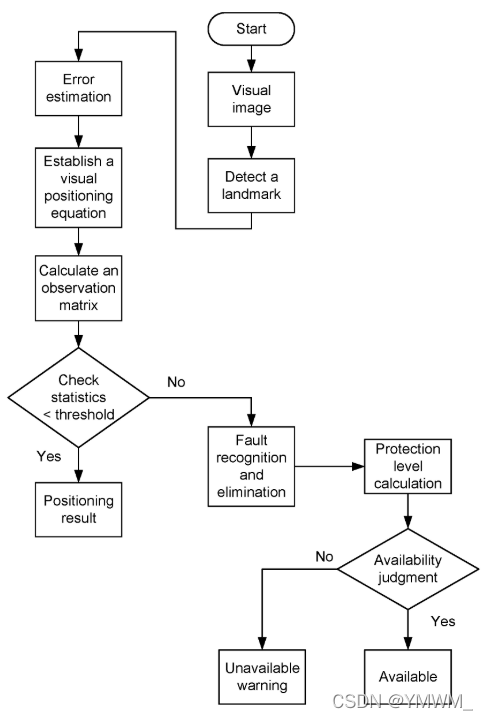
该方法通过引入视觉导航着陆系统的视觉观测来提高导航完好性监测的性能。如图1所示，是本实例中视觉完好性监测的流程图。首先，根据相机捕捉到的图像进行图像预处理，检测并保留带有着陆路标点的图像，用于视觉系统的定位。其次，为了保证定位精度，减少系统参数引起的误差，需要对误差进行修正和估计。然后，通过构建视觉定位方程，得到视觉观测模型，并计算观测矩阵，进一步计算飞机的位置和姿态信息。最后进行故障检测和排除，当检验统计量小于阈值时，系统没有发生故障，可以直接输出定位结果。否则，当检验统计量大于或等于该阈值时，表示系统发生故障，可以排除故障，并分别计算不同故障情况下的保护水平，进一步判断系统的可用性。

该方法包括以下具体步骤：

（1）根据具体的视觉定位场景建立合适的视觉定位模型，计算出视觉定位方案。

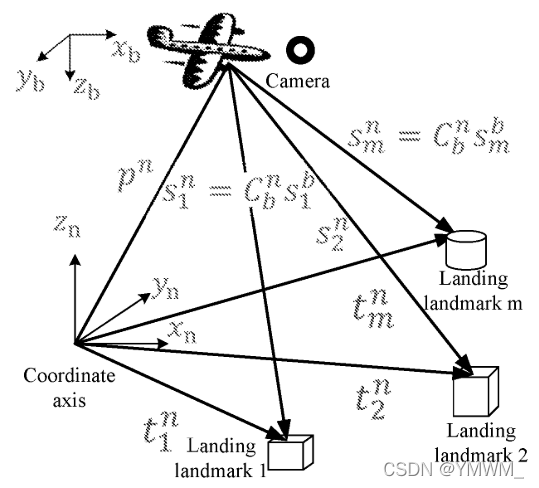
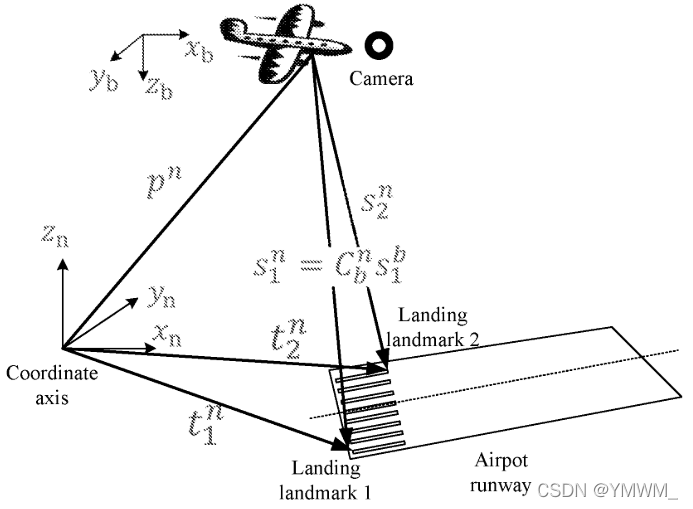
通过对飞机视觉着陆场景的研究，可以将视觉定位模型归纳为两种场景。第一种场景中，使用具有明显特征的人工目标作为着陆标志，如“H”或“I”标志，如图2所示。在第二种场景中，借用机场环境附近的机场跑道等高线，以便相机能够可靠地识别机场跑道目标，如图3所示。

如图2和图3所示，在一个导航坐标系中，根据向量相加，得到一个飞行器位置向量 $p^n$ ，相机和机身之间的小角度偏移向量 $q^n$ ，视线向量 $s_m^n$ ，它们相加以获得着陆路标向量 $t_m^n$ ，如下公式被建立：
$t_m^n=s_m^n+p^n+q^n$
因此，当相机系下路标点的视线向量 $s_m^c$ ，机体系下相机的位置 $q^b=[x_1\ y_2\ z_3]$ 和着陆路标点的位置向量 $t_m^n=[x_2\ y_2\ z_2]^T$ 已知时，可以通过计算获得飞机在三维世界中的位置 $p^n=[x_3\ y_3\ z_3]^T$ 。其中 $p^n$ 表示飞机在导航系下的位置向量； $t_m^n$ 表示第 $m$ 个路标点在导航系下的位置向量； $C_b^n$ 表示机体系到导航系的方向余弦矩阵； $s_m^n$ 表示第 $m$ 个目标在导航系中的视线向量； $s_m^b$ 表示第 $m$ 个目标在机体系下的视线向量， $s_m^n=C_b^ns_m^b$ ； $q^n$ 表示相机光心到飞机质心之间的距离； $q^b$ 表示相机在机体系下的位置，这可以通过标定获得。

（2）修正视觉系统参数误差，并计算误差状态向量。

由于系统参数容易产生误差，因此需要对视觉参数的误差进行估计和校正，以减少视觉观测计算中线性化误差的影响。基于上述数学参数的误差状态向量可以表示为：
$\delta x = [\beta p^n \ \delta t_m^n]$
其中 $\delta p^n$ 是飞机位置的三维误差向量，可以表示为：
$\delta p^n=\tilde{p}^n-p^n$
$\delta t_m^n$ 是路标点位置误差，可以表示为：
$\delta t_m^n=\hat{t}_m^n-t_m^n$
其中标称值用波浪线表示。

需要注意的是，当一个着陆路标进入和离开相机视野时，路标的数量实际上会随着时间而变化，但必须有一个合理的最大路标跟踪数量，以保持计算效率。

（3）建立视觉观测模型，计算视觉系统观测矩阵H。

如图2所示，第 $m$ 个路标点的视觉观测方程可以表示为：
$z_m(t_i)=T_c^{pix}\underline{s}_m^c(t_i)+v(t_i)$
该公式也称为伪距离定位方程，是基于着陆路标点和对应图像中的一个像素点得到的。其中 $z_m(t_i)$ 是着陆路标点 $m$ 的像素位置； $T_c^{pix}$ 是像素坐标系和相机坐标系之间的变换矩阵； $s_m^c$ 表示像素位置对应于从相机焦点向外延伸的视线向量； $s_{m_z}^c$ 是相机在 $s_z$ 方向上到光心的距离； $\underline{s}_m^c(t_i)$ 是相机到目标 $m$ 的视线向量的归一化形式； $v(t_i)$ 是独立加性高斯白噪声，其均值为0，方差为 $R$ ，它满足如下方程：
$E[v(t_i)v^t(t_j)]=\begin{cases} R, \ \ t_i=t_j \\ 0, \ \ \ t_i \neq t_j \end{cases}$

$T_{pix}^c$ 是已知的，设在一个高 $H$ 宽 $W$ 的矩形像素网格 $(M\times N)$ 中，像素坐标系与相机坐标的变换关系为 $T_c^{pix}$ ，它满足如下公式：
$T_{pix}^c=\begin{bmatrix} -\frac{H}{fM} & 0 & \frac{H(M+1)}{2fM} \\ 0 & \frac{W}{fN} & -\frac{W(N+1)}{2fN} \\ 0 & 0 & 1 \end{bmatrix}=(T_c^{pix})^{-1}$

为了便于计算，对非线性方程 $z_m(t_i)=T_c^{pix}\underline{s}_m^c(t_i)+v(t_i)$ 进行了线性化，一个非线性函数被设为 $h[x(t_i)]=T_c^{pix}\underline{s}_m^c(t_i)$ ，计算了一阶泰勒级数展开式，得到视觉系统观测矩阵 $H$ ，其中 $H$ 中的元素由下式计算的偏导数给出：
$H=[\frac{\partial h}{\partial p^n} \ 0]$
因为，
$q^n=C_b^nC_c^bs_m^c+C_b^nq^d=C_b^n(C_c^bs_m^c+q^d)$
$h$ 相对于 $p^n$ 的偏导数为：
$\frac{\partial h}{\partial p^n}=\frac{1}{s_{m_z}^c}T_c^{pix}(s_m^cC_n^bC_b^c-C_n^bC_b^c)$
因为 $H$ 与 $t_m^n$ 无关， $H$ 对 $\delta t_m^n$ 的偏导数为零。

（4）引入状态向量 $x$ 的视觉观测模型，表示为：
$z = H x + v + b$
其中 $z$ 是视觉观测向量；状态向量 $x$ 是 $n$ 维列向量； $v$ 是 $m$ 维观测噪声向量，它服从零均值协方差为 $R$ 的高斯分布，表示为 $R=\sigma^2I_{m*m}$ ； $b$ 是 $m$ 维故障偏差向量，在无故障情况下， $b$ 是一个零向量，当第 $i$ 个测量发生故障时， $b$ 中第 $i$ 个元素仍然表示为 $b$ 。

当视觉观测向量变化时，视觉观测误差表示为：
$\delta z=H \delta x$
因此，关于 $z = H x + v + b$ 的最小二乘解为，
$\delta x =(H^TH)^{-1}H^T\delta z$

如果不考虑噪声向量，则由状态向量 $x$ 的线性观测模型可得，
$\delta x=\hat{x}-x=\bar{H}z=\bar{H}b$
其中 $\bar{H}=(H^TH)^{-1}H^T$ 。

由于故障偏差向量 $b$ 对像素点 $(x, y)$ 的每个分量 $x$ 和 $y$ 都有影响，因此故障偏差向量 $b$ 在极坐标下表示为：
$b_i=||b||cos\theta$

$b_j=||b||sin\theta$

其中 $b_i=||b||cos\theta$ 是故障偏差向量 $b$ 对分量 $x$ 的影响； $b_j=||b||sin\theta$ 是故障偏差向量 $b$ 对分量 $y$ 的影响。

因此，位置误差的范数表示为：
$||\delta x||^2=(\bar{H}b)^T\bar{H}b$
依据如下公式：
$(\bar{H}b)^T\bar{H}b=b^T\bar{H}^T\bar{H}b=b_ib_i(\bar{H}^T\bar{H})_{ii}+b_ib_j(\bar{H}^T\bar{H})_{ij}+b_ib_j(H^TH)_{ji}+b_jb_j(\bar{H}^T\bar{H})_{jj}$

将其代入极坐标公式，可得到故障偏差向量 $b$ 对水平位置误差的影响公式，具体公式如下：
$\delta x=(||b||^2(sin^2\theta(\bar{H}^T\bar{H})_{ii}+sin2\theta(\bar{H}^T\bar{H})_{ij}+cos^2\theta(\bar{H}^T\bar{H})_{jj}))^{\frac{1}{2}}$
因此，当角度值 $\theta$ 发生变化时，水平位置误差也会发生相应的变化，特别是当取一些特殊的角度值时，水平位置误差 $\delta x$ 公式可以简化。

（5）结合视觉系统观测方程和卫星定位方程，计算组合导航定位方程。

假设卫星定位方程为 $z = G x$ ，合并视觉系统观测矩阵 $H$ 和卫星观测矩阵 $G$ 可以获得扩展观测矩阵 $H^{'}$ ，表示如下：
$H'=\begin{bmatrix} H \\ G \end{bmatrix}$
其中 $H^{'}$ 是 $m\times n$ 的线性观测矩阵。

当仍然有有限数量的卫星可用时，可以利用有限数量的卫星观测来加强视觉导航设备。如果视觉系统是由两个或三个相机组成的系统，则视觉系统中单个相头传感器的变换矩阵 $M_1$ 、 $M_2$ 和 $M_i$ 可以组合为 $M$ ， $M$ 可以具体表示为：
$M=\begin{bmatrix} M_1 & 0 & 0\\ 0 & M_2 & 0 \\ 0 & 0 & M_i \end{bmatrix}$

（6）在不同的故障模式下计算保护水平。

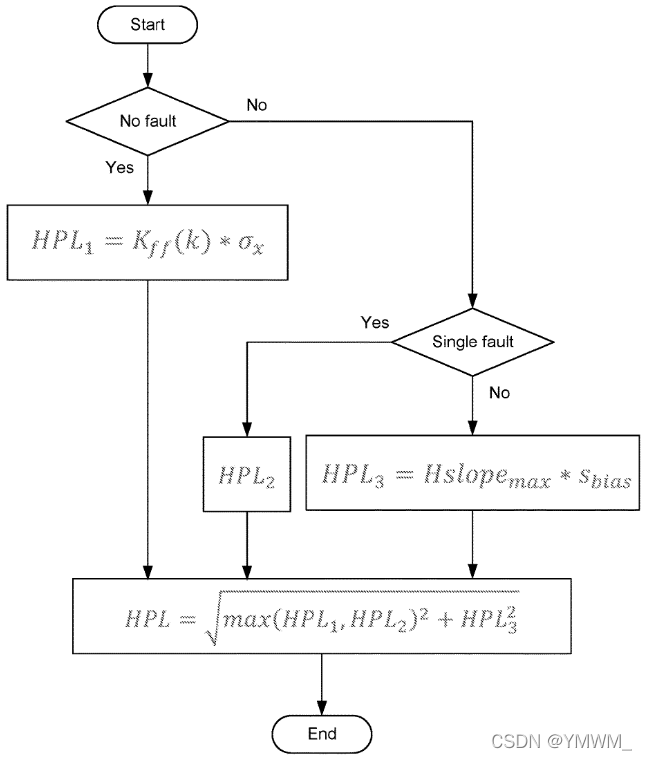
保护水平的计算方法分为三个假设：假设1、假设2和假设3。

假设1为观测无故障的情况，此时保护水平可根据无故障放大因子 $K_{ff}$ 和水平位置标准差 $\sigma_x$ 计算，其中无故障放大因子 $K_{ff}$ 由无故障概率 $P_{ff}$ 确定。因此，无故障保护水平的计算公式为：
$HPL_1=K_{ff}(k)*\sigma_x$
其中 $HPL_1$ 表示无故障情况下的保护水平； $K_{ff}$ 是无故障放大因子； $\sigma_x$ 是飞机在水平方向上的标准差。

假设2是观测中出现单故障的情况，在这种情况下，单个视觉观测或GNSS观测都有可能发生故障。当只有一个观测故障时，故障偏差向量 $b$ 中只包含一个偏差分量，此时水平位置误差 $\delta x$ 可表示为：
$\delta x=\hat{x}-x=\bar{H}z=\bar{H}b$
其中 $\hat{x}$ 表示最小二乘估计值， $\bar{H}=(H^TH)^{-1}H^T$ 。每个观测的斜率设为 $H s l o p e$ ，表示为：
$Hslope_i=\frac{\delta x^2}{D}=\frac{||\delta x||^2}{||p||^2}=\frac{\delta x^T \delta x}{p^Tp}=\frac{b^T\bar{H}^T\bar{H}b}{b^TP^TPb}$
其中 $b^T\bar{H}^T\bar{H}b=b_ib_i(\bar{H}^T\bar{H})_{ii}+b_ib_j(\bar{H}^T\bar{H})_{ij}+b_ib_j(\bar{H}^T\bar{H})_{ji}+b_jb_j(\bar{H}^T\bar{H})_{jj}$ ； $D$ 是统计检验量； $p$ 是奇偶向量； $P$ 是奇偶变换矩阵， $p = P b$ 。因此，水平定位误差保护水平 $HPL_2$ 为：
$HPL_2=Hslope_{max}\times s_{bias}$
其中
$s_{bias}=\sigma \frac{\sqrt{\lambda}}{\sqrt{n-4}}$
$\sigma$ 是噪声方差，它是一个分布参数。当无故障时， $HPL_2$ 的值最小；当观测中出现单故障时， $HPL_2$ 的值会增加。

假设3为观测出现两个故障的情况，出现两个视觉观测故障、两个GNSS观测故障或一个视觉观测和一个GNSS观测故障的情况。当两个观测故障时，第 $i$ 个观测与第 $j$ 个观测同时故障的故障偏差向量为 $b (i)$ 和 $b (j)$ ，可表示为：
$b=[0\ \cdots \ 0\ b^{(i)} \ b^{(j)} \ \cdots \ 0\ 0 \cdots \ 0] ^T$
因此，定位误差表示如下：
$\Delta=\bar{H}b=Ab=[b^{(i)}A_{1i}+b^{(j)}A_{1j}b^{(i)}A_{2i}+b^{(j)}A_{2i}b^{(i)}A_{3i}+b^{(j)}A_{3i}b^{(i)}A_{4i}+b^{(j)}A_{4j}]^T$
水平定位误差表示如下：
$\delta x^2=(b^{(i)}A_{1i}+b^{(j)}A_{1j})^2+(b^{(i)}A_{2i}+b^{(j)}A_{2j})^2$
因此，计算 $H s l o p e$ 如下：
$Hslope_i=\frac{\delta x^2}{D}=\frac{||\delta x||^2}{||p||^2}=\frac{\delta x^T \delta x}{p^Tp}=\frac{(b^{(i)}A_{1i}+b^{(j)}A_{1j})^2+(b^{(i)}A_{2i}+b^{(j)}A_{2j})^2}{b^TP^TPb}$
因此，计算 $HPL_3$ 的公式如下：
$HPL_3=Hslope_{max}\times s_{bias}$

结合假设1、假设2和假设3，所有情况下的误差在保护水平中都被考虑，计算保护水平的公式如下，
$HPL=\sqrt{max(HPL_1,HPL_2)^2+HPL_3^2}$

在所有情况下，保护水平的值越准确，在给定风险值的情况下，用户越能避免所有偏差，系统可用性也就越高。根据本实例，通过所提出的视觉导航完好性监测算法，可以有效地排除故障，从而提高导航定位的准确性和可用性。上述实例仅仅是用于清楚说明的示例，而不是对实现方式的限制。那些具有一般技能的人也可以在上述描述的基础上做出其它不同形式的改变。没有必要也没有办法用尽所有的实现方式。其发生的变化或变更，仍在本发明的保护范围内。

本发明的其它实例可以很容易地结合本发明的描述和实践而被本领域中的技术人员理解。本描述和实例仅被认为是示例性的，本发明的真正范围和主题由权利要求书定义。