文章目录
1. Pooling的作用
- 下采样(Down-sampling),降维、去冗杂信息
- 扩大感受野(Enlarge the receptive field)
- 其实和卷积层的效果是类似的,只是卷积核变为了max函数,整体而言还是在扩大感受野
- 提取边缘信息
- 实现特征不变性invariance:translation、rotation、scale(平移、旋转和尺度不变性)
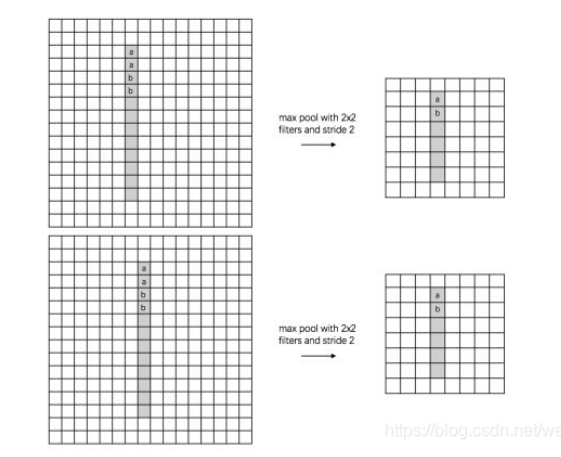
- 说明:上图表示不同水平/垂直位置的值进行池化操作值后得到的结果相同
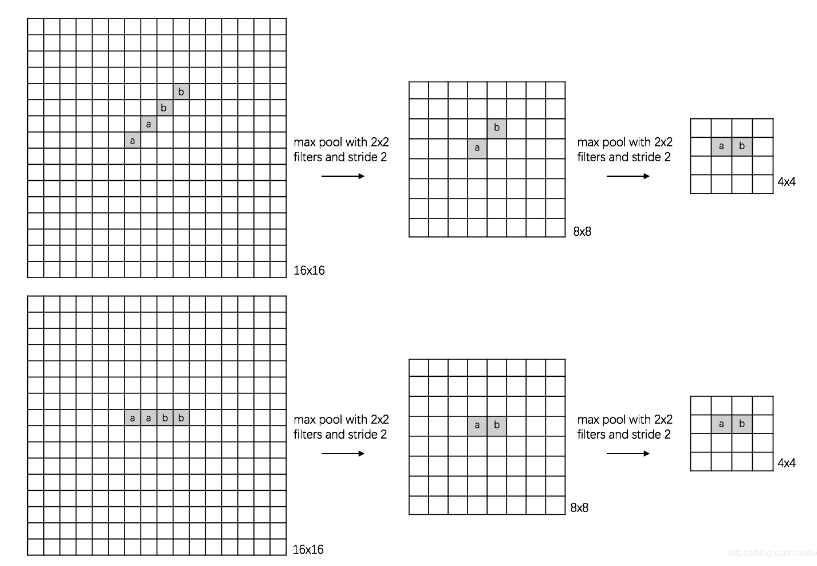
- 说明:上图表示不同方位角的特征图经过两次pooling之后得到的结果相同
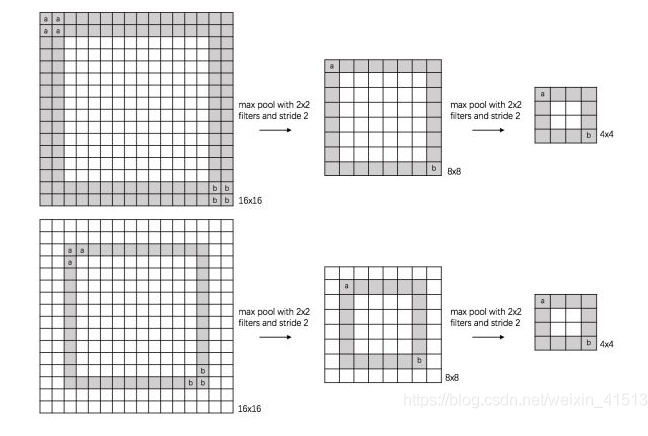
- 说明: 上图表示不同尺度的特征图经过pooling之后仍然得到了相同的结果
- 添加非线性,在一定程度上防止过拟合(看到max pooling其实第一个出现脑海中的应该有ReLu激活函数)
2. 各种不同的Pooling
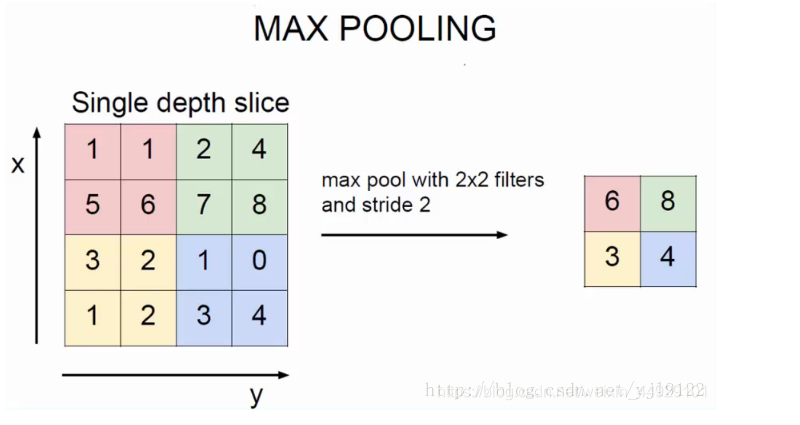
1. max pooling(最大池化层)
y
k
i
j
=
m
a
x
(
p
,
q
)
∈
R
i
j
x
k
p
q
y_{kij} = max_{(p,q) \in R_{ij}}x_{kpq}
ykij?=max(p,q)∈Rij??xkpq?
其中
y
k
i
j
y_{kij}
ykij?表示第k个特征图有关于矩形区域
R
i
j
R_{ij}
Rij?的最大池化层的输出值,
x
k
p
q
x_{kpq}
xkpq?表示矩形区域中位于位置
x
k
p
q
x_{kpq}
xkpq?的元素。
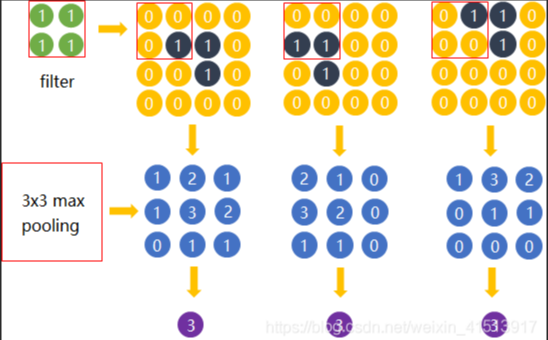
2. average pooling (平均池化层)
y k i j = 1 R i j ∑ ( p , q ) ∈ R i j x k p q y_{kij} = \frac{1}{R_{ij}}\sum_{(p,q)\in R_{ij}}x_{kpq} ykij?=Rij?1?(p,q)∈Rij?∑?xkpq?
- average pooling和max pooling的数值区别:
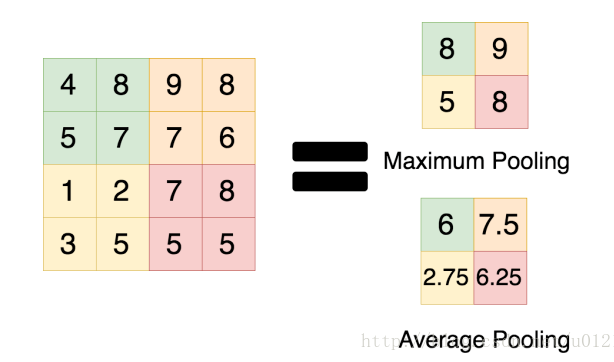
- 根据一些理论,特征提取的误差主要来源于:
- (1) 邻域大小受限而造成的估计值方差增大
- (2) 卷积层参数误差造成估计值均值偏移
- 一般而言,average-pooling 可以减小第一种误差,最大程度保留图像的背景信息,而max-pooling可以减小第二种误差,保留更多的纹理信息。
总结:
- 通常我们会倾向于使用max pooling,因为max-pooling在直觉上是在做特征选择,提取最明显的特征来代替整体;而average pooling更像是在做特征融合,将不同的特征进行融合在一起了,其实是模糊了一些强的特征。
3. Global Average Pooling(全局平均池化层)
M lin等人提出使用Global Average Pooling层替代最后的全连接层,用很小的代价实现了降维,其公式同average pooling,但是不用划分矩形区域,而是在整个特征图中进行操作
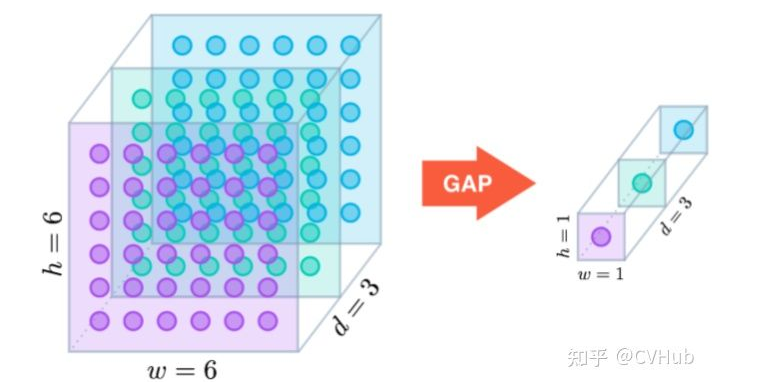
4. mix pooling(混合池化层)
y i j = λ . m a x ( p , q ) ∈ R i j x k p q + ( 1 ? λ ) . 1 ∣ R i j ∣ ∑ ( p , q ) ∈ R i j x k p q y_{ij} = \lambda . max_{(p,q)\in R_{ij}}x_{kpq} + (1-\lambda).\frac{1}{\vert R_{ij} \vert}\sum_{(p,q)\in R_{ij}}x_{kpq} yij?=λ.max(p,q)∈Rij??xkpq?+(1?λ).∣Rij?∣1?(p,q)∈Rij?∑?xkpq?
- 用随机过程替代常规的确定池化过程,在模型训练过程中随机选择max和average pooling方法进行池化,在一定程度上有助于防止过拟合
- 说明:mix/hybrid pooling方法比传统的max/average pooling方法是更优秀的,其需要的额外开销可以忽略不计,也不需要进行参数调整,可以较为广泛的应用于CNN。
5. stochastic pooling(随机池化)
过程如下:
- (1) 将矩形内元素除以其sum,得到概率矩阵(伪)
- (2) 按照概率选取矩阵内数据
- (3) 按照上面的概率随机采样选择内部数据
说明:
- 随机池化按照特征图内的数值大小进行概率划分,但是选择的数字并非最大值一成不变,而是根据概率选择,原则上仍然是数值越大概率越大,但是选择其他值的概率也存在,所以范化性也更好。
6. Local Importance-based pooling(局部重要性池化层)
用处:
- CNN通常使用下采样来缩小特征空间,但是在一些特别的任务中可能会丢失一些重要的细节,损失模型精度。使用regional pooling可以一定程度上缓和。操作为:在下采样的过程中自动增加特征判别功能
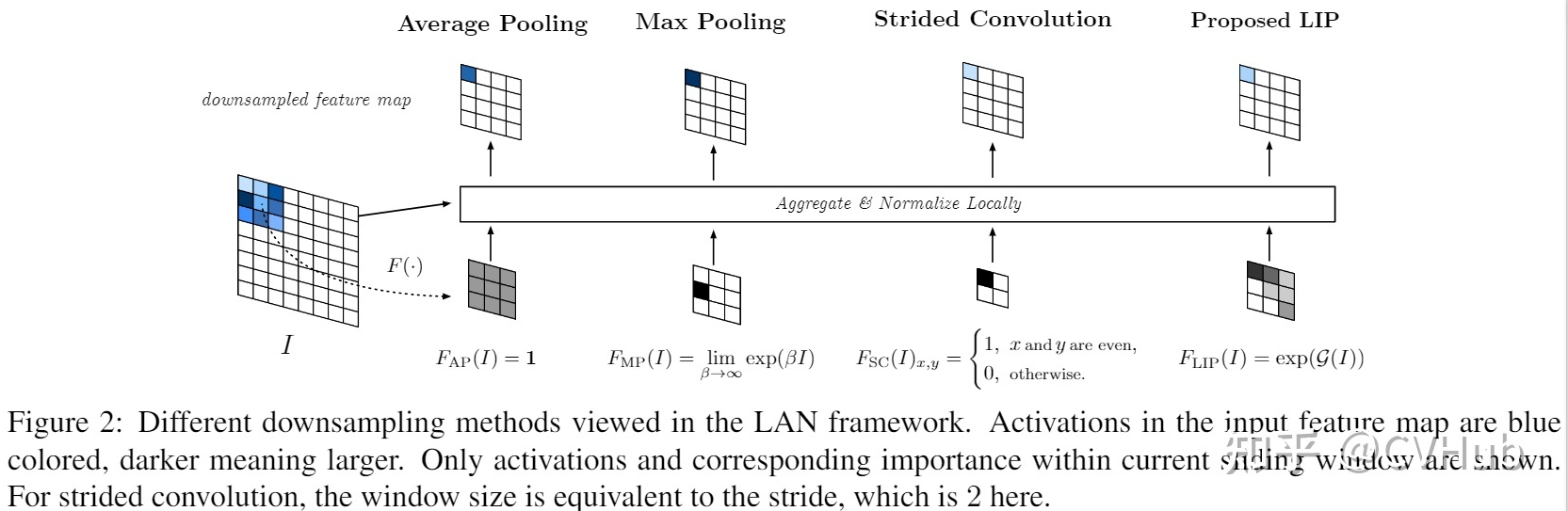
- 其中F的大小和特征I的大小一致,代表每一个点的重要性。
- 图中分别代表的是Average pooling、max pooling和stride为2的convolution。
- 最大池化对应的值不一定是具有最具区分力的特征
- 步长为2的卷积问题在于固定的采样位置
池化操作可以归纳为:
O
x
′
,
y
′
=
∑
(
Δ
x
,
Δ
y
)
∈
Ω
F
(
I
)
x
+
Δ
x
,
y
+
Δ
y
I
x
+
Δ
x
,
y
+
Δ
y
∑
(
Δ
x
,
Δ
y
)
∈
Ω
F
(
I
)
x
+
Δ
x
,
y
+
Δ
y
O_{x',y'} = \frac{\sum_{(\Delta x,\Delta y)\in\Omega}F(I)_{x+\Delta x,y+\Delta y}I_{x+\Delta x,y+\Delta y}}{\sum_{(\Delta x,\Delta y)\in \Omega}F(I)_{x+\Delta x ,y+ \Delta y}}
Ox′,y′?=∑(Δx,Δy)∈Ω?F(I)x+Δx,y+Δy?∑(Δx,Δy)∈Ω?F(I)x+Δx,y+Δy?Ix+Δx,y+Δy??
局部重要池化结构可以表示为:
O
x
′
,
y
′
=
∑
(
Δ
x
,
Δ
y
)
∈
Ω
I
x
+
Δ
x
,
y
+
Δ
y
e
x
p
(
G
(
I
)
)
x
+
Δ
x
,
y
+
Δ
y
∑
(
Δ
x
,
Δ
y
)
∈
Ω
e
x
p
(
G
(
I
)
)
x
+
Δ
x
,
y
+
Δ
y
O_{x',y'} = \frac{\sum_{(\Delta x,\Delta y)\in\Omega}I_{x+\Delta x,y+\Delta y}exp(G(I))_{x+\Delta x,y+\Delta y}}{\sum_{(\Delta x,\Delta y)\in \Omega}exp(G(I))_{x+\Delta x ,y+ \Delta y}}
Ox′,y′?=∑(Δx,Δy)∈Ω?exp(G(I))x+Δx,y+Δy?∑(Δx,Δy)∈Ω?Ix+Δx,y+Δy?exp(G(I))x+Δx,y+Δy??
- a. 下采样的位置需要尽可能地非固定间隔(使用conv替代pooling的问题)
- b. 重要性函数F需要通过学习获得
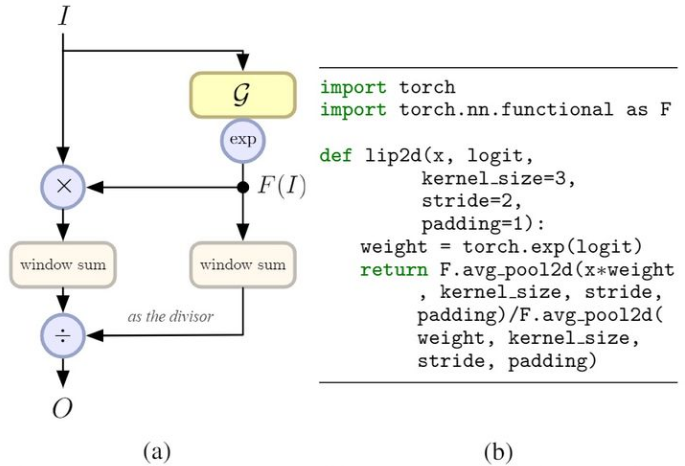
说明:
- Local importance pooling可以自适应和判别地进行特征图地特征汇集,丢弃冗余信息。极大地保存了物体地局部细节,对于细节敏感的任务至关重要。
7. Generalized-mean Polling layer(GeM池化层)
[ ( 1 ∣ R i j ∣ ∑ ( p , q ) ∈ R i j x k p q p ) 1 p ] [(\frac{1}{\vert R_{ij} \vert} \sum_{(p,q) \in R_{ij}} x_{kpq}^p)^{\frac{1}{p}}] [(∣Rij?∣1?(p,q)∈Rij?∑?xkpqp?)p1?]
- 当p = 1的时候, 相当于平均池化
- 当p = ∞ \infty ∞的时候,相当于最大池化
说明:
- 其中的参数p是可以学习的一个参数,可以通过数据学习到一个比较合适的结果
3. 使用卷积替代池化
1. average pool
conv本身就相当于在求和,求对应的平均值即可(或者直接sum pooling也是一样),如果kernel = 2,stride = 2不加任何其他操作就等价于stride = 2的average pooling了
2. max pool
原理:
C
o
n
v
+
R
E
L
U
=
M
a
x
P
o
o
l
i
n
g
Conv + RELU = Max Pooling
Conv+RELU=MaxPooling
可以看到,如果我们使用conv然后加上一个relu激活函数,其得到的结果完美等价于max pooling
4. 是否需要池化操作
-
卷积操作对位置是非常敏感的,而池化操作可以缓解这种敏感性

-
具体问题具体分析吧,增加一个卷积层就操作而言其实是更加简单的,而且效果也和max pooling操作相类似,所以一般情况下是可以不用max pooling的,但是对于一些具体的操作而言是一个trade off的问题。
