一、针孔相机模型

在这里插入图片描述

如图所示为针孔相机模型， $O_{cam}-X_{cam}-Y_{cam}-Z_{cam}$ 为相机坐标系， $O_{cam}$ 为相机光心，习惯上，让 $Z_{cam}$ 轴指向相机拍摄朝向的正前方， $X_{cam}$ 轴向右（从 $Z_{cam}$ 轴负方向，向正方向看）， $Y_{cam}$ 轴向下。

$O_o-X-Y$ 为物理成像平面，位于 $Z_{cam}$ 轴负方向，距离相机光心 $f$ 处， $f$ 为相机焦距。

二、内参数矩阵

相机坐标系内一点 $M$ 的坐标为 $x_{cam},y_{cam},z_{cam})$ ，经过上述针孔相机模型后，投影到成像平面上一点 $m$ ，坐标为 $(x, y)$ 。

从 $Y_{cam}$ 轴负方向朝正方向看（上图中，从上往下看），有如下相似三角形关系：
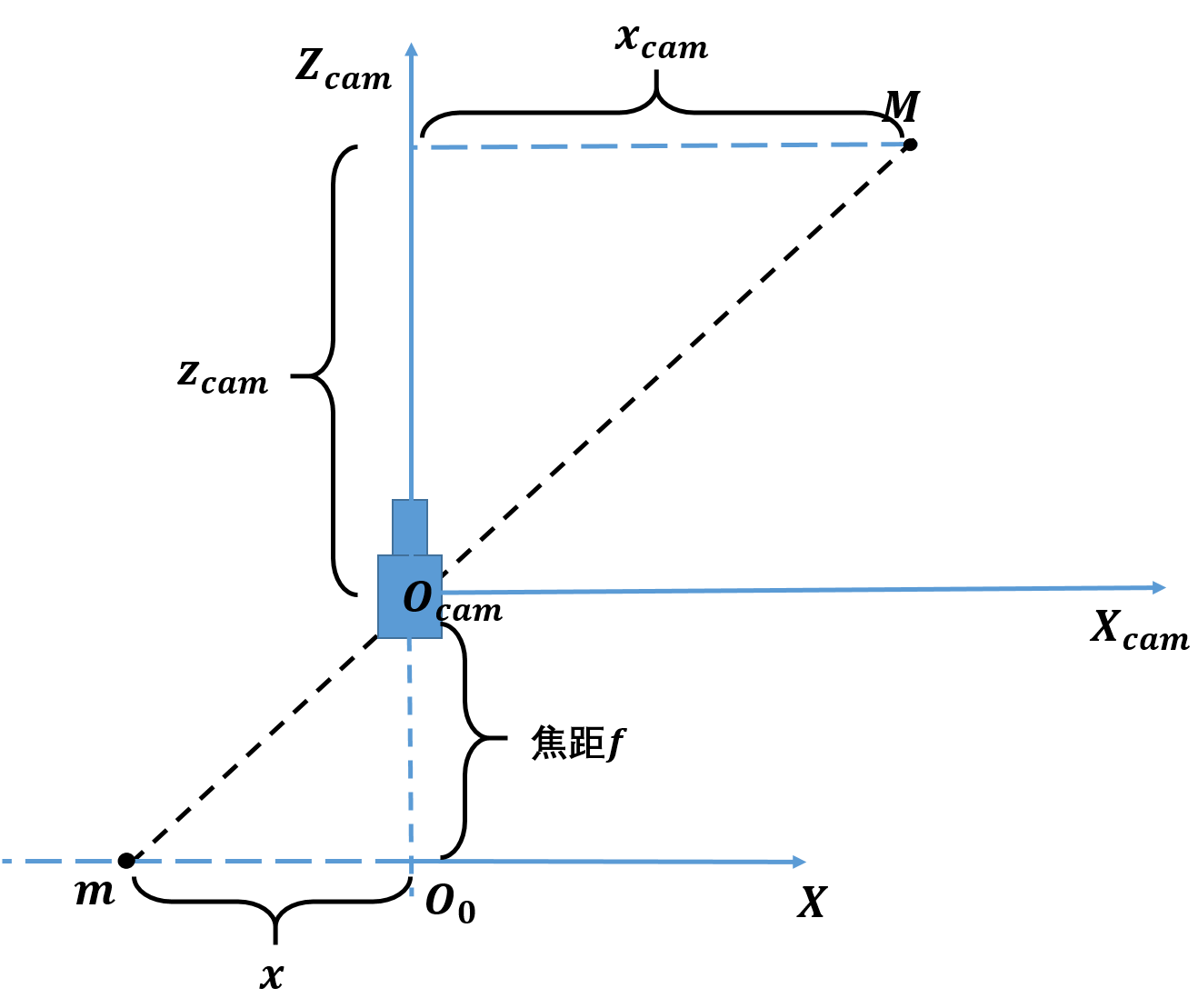
在这里插入图片描述
根据三角形相似关系，有：
$\frac{z_{cam}}{f}=\frac{x_{cam}}{-x}$
同理，也会有：
$\frac{z_{cam}}{f}=\frac{y_{cam}}{-y}$

公式中的负号是因为针孔成像所成的像是倒像，

在坐标的表现上就是位于 $X_{cam}$ 正半轴的点经过投影后，会被投影到 $X$ 负半轴；

位于 $Y_{cam}$ 正半轴的点经过投影后，会被投影到 $Y$ 负半轴。

为了将公式中的负号去掉，使式子更加简洁，人们将成像平面对称到摄像机前方，如下图所示：
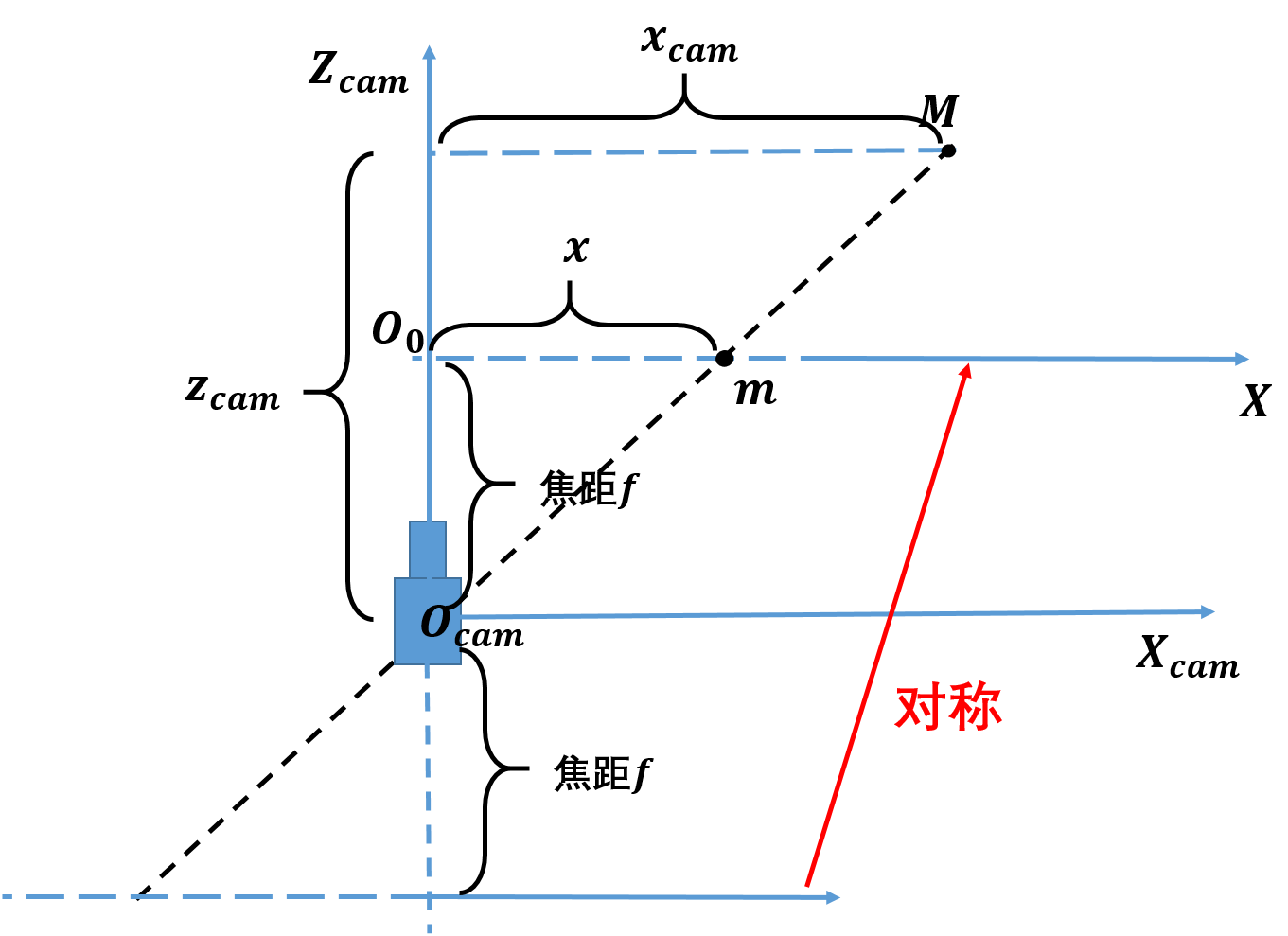
在这里插入图片描述
公式中的负号被去掉：
$\frac{z_{cam}}{f}=\frac{x_{cam}}{x}\tag{1}$
同理，也会有：
$\frac{z_{cam}}{f}=\frac{y_{cam}}{y}\tag{2}$
整理，将 $x, y$ 放到同一侧：
$x=f\frac{x_{cam}}{z_{cam}}\tag{3}$
$y=f\frac{y_{cam}}{y_{cam}}\tag{4}$

此时，所有变量仍是以长度为单位，比如毫米，如可以说焦距 $f$ 是5毫米。

但实际上，相机最后拍摄得到的相片是由一个个像素点组成的，所以我们还需要将物理成像平面坐标系转变成像素坐标系，通常像素平面坐标系的原点会被定义在物理成像平面的左上角，横轴、纵轴与物理成像平面坐标系的横轴、纵轴平行，如下图所示：
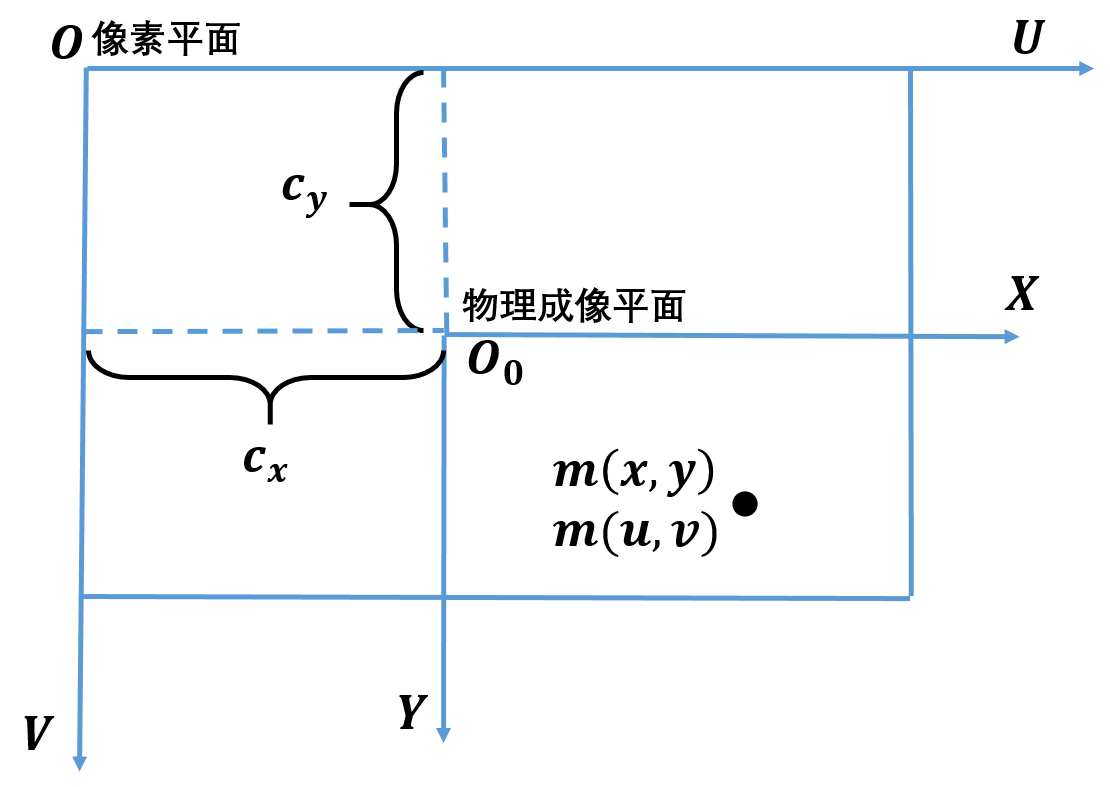
在这里插入图片描述
为将长度单位转换成像素单位，定义了两个参数 $α, β$ ，单位为 $像素 / 米$ ，用以表征每个像素的尺寸，具体意义是一米的长度内，由多少个像素组成，属于与相机生产时的硬件相关的参数，如下图举例所示：
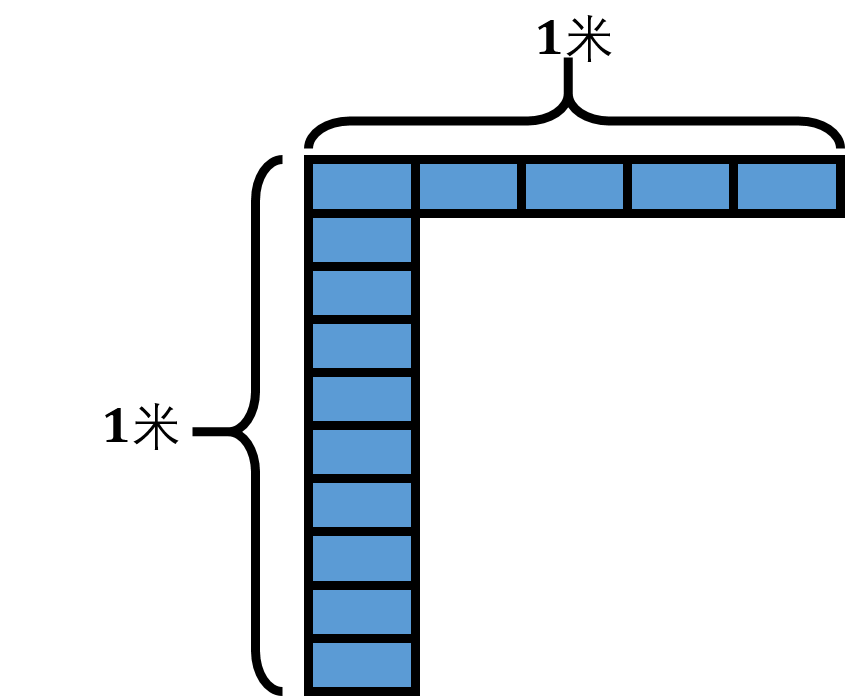
在这里插入图片描述
横轴方向上，5个像素的长度为1米，所以 $α = 5 像素 / 米$ ，纵轴方向上，10个像素的长度为1米（像素可以不是正方形），所以 $β = 10 像素 / 米$ 。

于是，物理成像平面上的坐标与像素平面上的坐标的转换关系如下：
$u=αx+c_x\tag{5}$
$v=βy+c_y\tag{6}$
其中， $c_x,c_y$ 为物理成像坐标系的原点相对于像素坐标系的原点的偏移量，单位是 $像素$ 。

将公式3、4代入5、6，可得：
$u=fα\frac{x_{cam}}{z_{cam}}+c_x$
$v=fβ\frac{y_{cam}}{z_{cam}}+c_y$
令 $fα=f_x$ ， $fβ=f_y$ 得：
$u=f_x\frac{x_{cam}}{z_{cam}}+c_x\tag{7}$
$v=f_y\frac{y_{cam}}{z_{cam}}+c_y\tag{8}$

通过齐次坐标形式，将式7、8转换成简洁的矩阵形式：
像素坐标 $(u, v)$ 的齐次坐标形式为 $(u, v, 1)$
$\begin{bmatrix} u \\ v \\ \end{bmatrix} →\begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix}=\begin{bmatrix} f_x\frac{x_cam}{z_cam}+c_x \\ f_y\frac{y_cam}{z_cam}+c_y \\ 1 \\ \end{bmatrix}$
两边乘上 $z_{cam}$ ：
$z_{cam}\begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix}=\begin{bmatrix} f_xx_{cam}+c_xz_{cam} \\ f_yy_{cam}+c_yz_{cam} \\ z_{cam} \\ \end{bmatrix}=\begin{bmatrix} f_x&0&c_x&0 \\ 0&f_y&c_y&0 \\ 0&0&1&0\\ \end{bmatrix}\begin{bmatrix} x_{cam}\\ y_{cam}\\ z_{cam}\\ 1\\ \end{bmatrix}$
最终得到：
$z_{cam}\begin{bmatrix} u \\ v \\ 1 \\ \end{bmatrix}=\begin{bmatrix} f_x&0&c_x&0 \\ 0&f_y&c_y&0 \\ 0&0&1&0\\ \end{bmatrix}\begin{bmatrix} x_{cam}\\ y_{cam}\\ z_{cam}\\ 1\\ \end{bmatrix}\tag{9}$

式9完成了将相机坐标系上的坐标 $x_{cam},y_{cam},z_{cam})$ 转换成像素平面上的坐标 $(u, v)$ 的任务

令 $K=\begin{bmatrix} f_x&0&c_x&0 \\ 0&f_y&c_y&0 \\ 0&0&1&0\\ \end{bmatrix}$ ，便是相机内参数矩阵。

其中包含了几个相机的硬件信息， $f$ 焦距，长度单位，如mm； $c_x,c_y$ 成像平面坐标系原点相对于像素平面坐标系原点的偏移量，像素单位； $α ， β$ 单位长度上的像素个数，单位如：像素/mm。

注意： $z_{cam}$ 实际上是三维空间点的深度信息，在投影过程中丢失了，而三维重建工作的很大一部分任务都是设法还原这个深度信息。
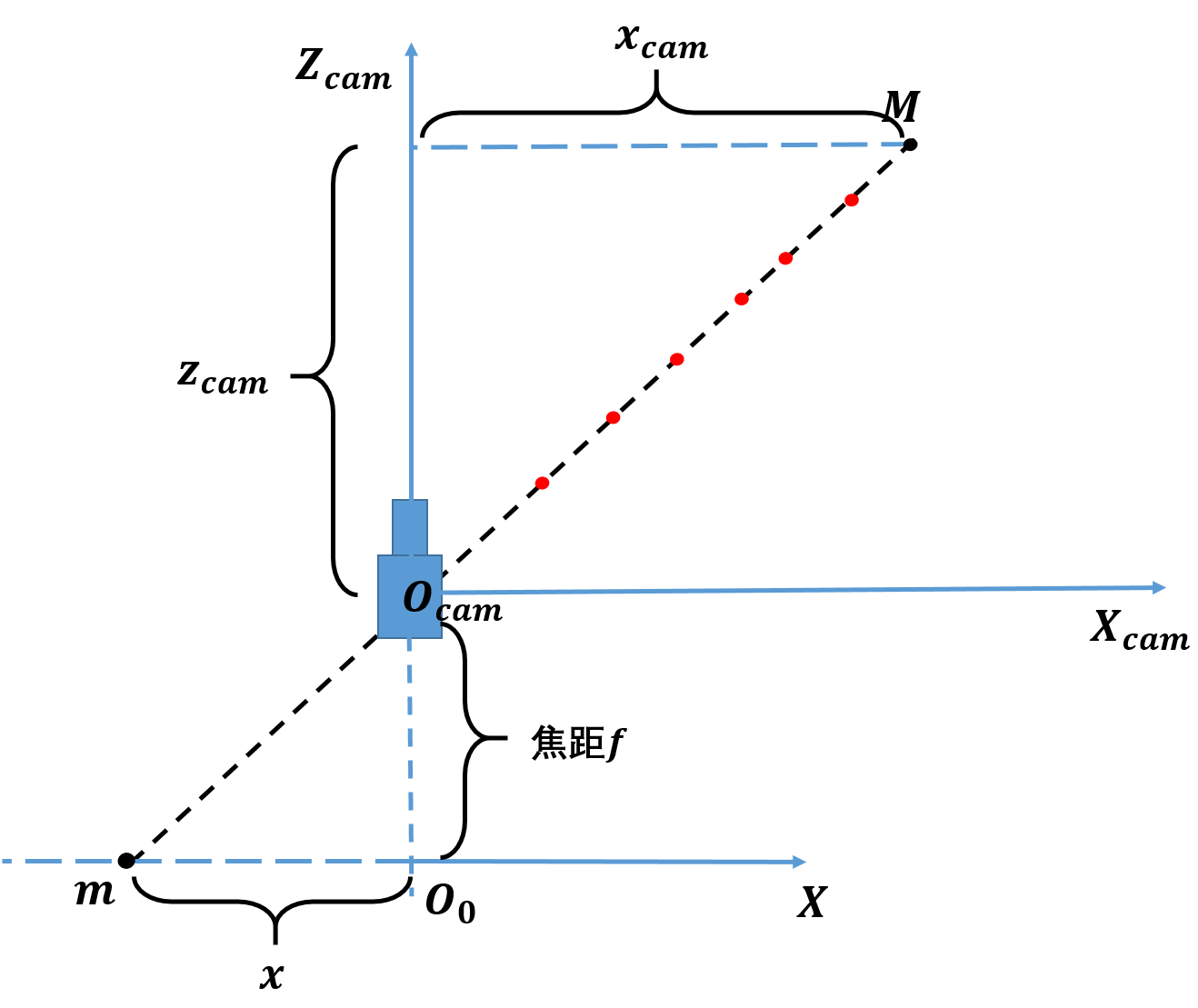
在这里插入图片描述
举个例子来说，像素坐标系上得到的一个投影点 $m$ ，实际上只能知道它是由射线 $O M$ 上的任意一个点投影得到的，但单纯从这个投影关系来说，是无法知道具体是射线 $O M$ 上的哪个具体位置的点投影过来得到的投影点 $m$ ，因为整条射线 $O M$ 上的所有点（无穷多个）只要投影到像素坐标系上，都会重叠在 $m$ 处。