1 过拟合问题

过拟合是数据科学领域的一个重要问题，需要处理好过拟合问题才能建立一个健壮和准确的模型。当模型试图很好的拟合训练数据但导致无法泛化到测试数据时，就出现了过拟合。过拟合模型捕捉的更多的是训练数据找的呢细节和噪声，而不是模型的整体趋势。因此，即使特征的细微变化也会极大的改变模型的结果。这就导致过拟合模型在训练数据上表现的很出色，但在测试数据上表现不佳。
为了便于理解，我们模拟模型的训练过程，实际上模型训练的过程就是不断迭代直到找到一个方程 $y = f (x)$ 来拟合数据集。但是怎么去衡量模型拟合的好坏呢？如下图所示是使用三个方程来拟合一个数据及的结果。
在这里插入图片描述
在这里，我们有一个 2 次多项式拟合和两个不同的 8 次多项式，他们的方程如下：

由上可知，第一个（“更简单”的函数）很可能会更好地泛化到新数据，而第三个（更复杂的函数）显然会过度拟合训练数据。

2 正则化解释

过拟合的主要原因是模型的复杂性。因此，我们可以通过控制模型的复杂性来防止过拟合，这正是正则化所做的。正则化通过惩罚模型中的较高项来控制模型的复杂性。模型中添加正则项之后，会最小化模型的损失和复杂性。正则化的基本本质是在损失函数中添加一个惩罚项。

以线性回归为例，我们的损失由均方误差 (MSE) 给出：
$\mathcal{L}(\mathbf{w})=\frac{1}{m} \sum_{i=1}^{m}\left(y_{i}-\hat{y}_{i}\right)^{2}$
我们的目标是最小化这种损失：
$\min _{\mathbf{w}} \mathcal{L}(\mathbf{w})=\min _{\mathbf{w}} \frac{1}{m} \sum_{i=1}^{m}\left(y_{i}-\hat{y}_{i}\right)^{2}$
为了防止过拟合，我们希望增加对不太复杂的函数的偏向。也就是说，给定两个可以很好地拟合我们的数据的函数，我们更喜欢更简单的一个。我们通过添加一个正则化项来做到这一点，通常是 L1 范数或平方 L2 范数：
$\text { L1 正则化: }\|\mathbf{w}\|_{1}=\sum_{i}^{n}\left|w_{i}\right|$ $\text { L2 正则化: }\|\mathbf{w}\|_{2}^{2}=\sum_{i}^{n} w_{i}^{2}$

假设将平方 L2 范数添加到损失中并最小化，我们得到岭回归（ Ridge regression）：
$\min _{\mathbf{w}} \mathcal{L}_{\lambda}(\mathbf{w})=\min _{\mathbf{w}}\left(\lambda\|\mathbf{w}\|_{2}^{2}+\frac{1}{m} \sum_{i=1}^{m}\left(y_{i}-\hat{y}_{i}\right)^{2}\right)$
其中 λ 是正则化系数，它决定了我们想要多少正则化。λ的取值很重要，如果λ太大，模型会变得太简单并且容易欠拟合。如果λ太小，惩罚项的影响变得忽略不计，模型很容易过拟合。如果λ设置为0，则正则化完全被删除（过拟合高风险）。

Note： 套索回归（Lasso regression）使用L1正则化，岭回归（ Ridge regression）使用L2正则化，弹性网络回归（Elastic net regression）包含了L1和L2两种正则化。因此引入了一个新的超参数 $\alpha$ ，它管理要包含的每个 L1 或 L2 惩罚的比率。计算公式如下：
$Elastic\ net\ penalty\ =\ \alpha\ast L_{1\ penalty}+\left(1-\alpha\right)\ast L_{2\ penalty}$

3 不同的正则项的区别？

一般正则项是以下公式的形式：
$\frac{1}{N}\sum_{i=1}^N\left(y_i-\hat{y}_{i}\right)^2+\lambda\sum_{i=1}^M\left|w_i\right|^q$
其中M是模型的阶数，q是正则项的阶数。高维度的模型图像表征非常难以理解，那就使用二维模型来理解。这里令M=2，令q=0.5、q=1 、q=2和q=4 有：
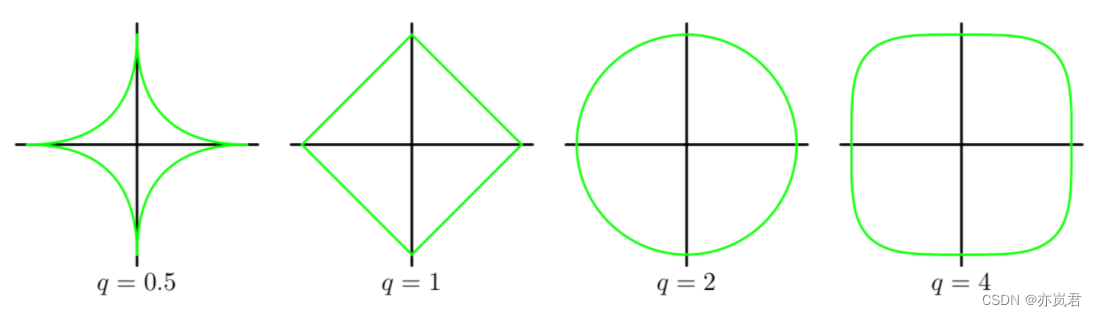
在这里插入图片描述
其中横纵坐标分别为 $\theta_1$ 和 $\theta_0$ ，绿色线表示的是等高线的一条，其z轴坐标为 $\lambda\sum_{i=1}^M\left|w_{i}\right|^{q}$ 。
下图展示的为它们的三维图：

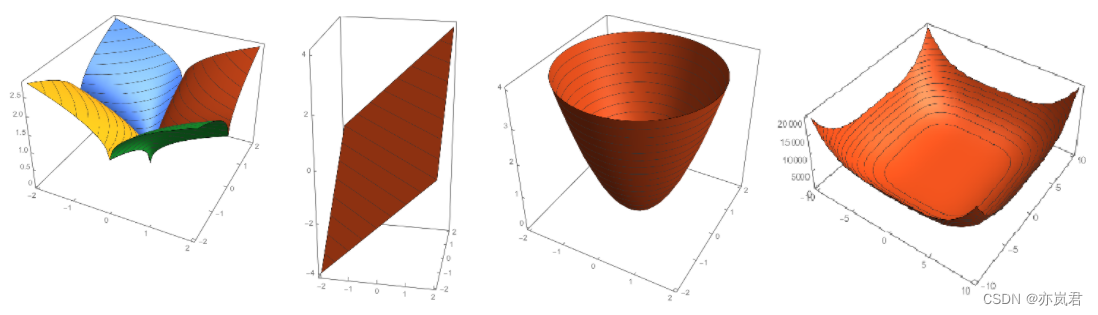
接下来，我们把q=1（右图）和q=2（左图）代价函数（损失函数+正则项）表示如下图所示。
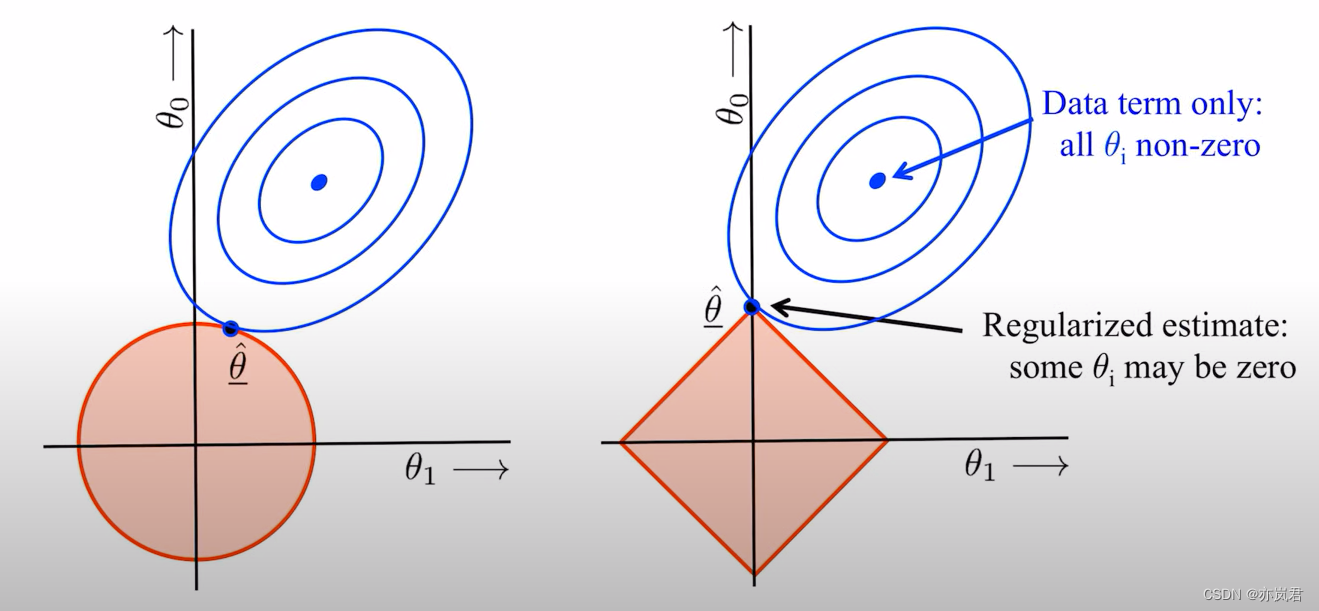
在这里插入图片描述
根据上面的解释我们知道了红色圈代表的是正则项，红圈收缩的过程就是加大惩罚力度的过程。
但蓝色圈代表什么呢？蓝色圈是损失函数，一圈一圈表示他的登高线，他会根据最小二乘或梯度下降从中间的圈不断向外圈走。
所以上图可以简单的理解为：最小化损失函数就是求蓝色圈+红色圈的和的最小值，而这个值通在很多情况下是两个曲面相交的地方。

下面我们以L1和L2正则化来做详细比较：
由下图可知，L1和L2都随着 w 的绝对绝对值的增加而增加。然而，L1以恒定速率增加，而L2呈指数增长。因为我们知道，在进行梯度下降时，我们将根据损失函数的导数更新权重。因此，如果我们在损失函数中包含了正则化，则正则化的导数将决定权重如何更新。
对于L1正则化，斜率是恒定的。这意味着随着 w 变小，更新不会改变，所以我们不断获得相同的“奖励”来使权重更小，从而最终使权重为零。所以L1正则化也称为稀疏正则化，它用于处理主要由零组成的稀疏向量。这说明了L1正则化自带特征选择的功能，这一点十分有用。
对于L2正则化，随着 w 变小，范数的斜率也会变小，这意味着更新也会变得越来越小。当权重接近 0 时，更新将变得非常小，几乎可以忽略不计，因此权重不太可能变为 0。
在这里插入图片描述
L1正则化和L2正则化在实际应用中的比较:
L1在确实需要稀疏化模型的场景下，才能发挥很好的作用并且效果远胜于L2。在模型特征个数远大于训练样本数的情况下，如果我们事先知道模型的特征中只有少量相关特征（即参数值不为0），并且相关特征的个数少于训练样本数，那么L1的效果远好于L2。然而，需要注意的是，当相关特征数远大于训练样本数时，无论是L1还是L2，都无法取得很好的效果。