[人工智能] nn.PReLU()和nn.ReLU

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> nn.PReLU()和nn.ReLU -> 正文阅读

[人工智能]nn.PReLU()和nn.ReLU

1、nn.PReLU()

nn.PReLU(
    num_parameters: int = 1,
    init: float = 0.25,
    device=None,
    dtype=None,
)

PReLU的公式：

$\text{PReLU}(x) = \max(0,x) + a * \min(0,x)$

或者：

$\text{PReLU}(x) = \begin{cases} x, & \text{ if } x \geq 0 \\ ax, & \text{ otherwise } \end{cases}$

其中a代表的是可学习的参数：

（1）当不带参数时（nn.PReLU()），PReLU就使用一个a计算所有通道，即所有通道对应同一个a；

（2）当有参数时（nn.PReLU(nchannels)），PReLU在每个通道使用不同的a；

通道dim是input的第二个dim。当输入的 dims < 2 时，没有通道 dim 且通道数 = 1。同时输入和输出的形状是一样的。

PReLU()参数解析：

num_parameters：表示学习的参数，只有两个值是合法的，默认为1，或者是输入的通道数
init：a的初始值，默认为0.25；
device:None
dtype:None

m = nn.PReLU()
input = torch.randn(4)
print(input)
output = m(input)
print(output)

tensor([-0.6559, -0.3400, -0.5796,  1.2480])
tensor([-0.1640, -0.0850, -0.1449,  1.2480], grad_fn=<PreluBackward0>)

m = nn.PReLU(2)
input = torch.randn([2,2])
input.unsqueeze(0)
print(input)
output = m(input)
print(output)

tensor([[-0.7314,  0.0393],
        [ 0.0932, -0.7079]])
tensor([[-0.1828,  0.0393],
        [ 0.0932, -0.1770]], grad_fn=<PreluBackward0>)

2、nn.ReLU()

nn.ReLU(inplace: bool = False)

$\text{ReLU}(x) = (x)^+ = \max(0, x)$

inplace: 即原地操作符，直接在原来的内存上改变变量的值，这里是默认False

相比PReLU是没有可学习的参数a；同样它的输入和输出的形状是保持一致的；

m = nn.ReLU()
input = torch.randn(2)
print(input)
output = m(input)
print(output)

tensor([-0.0453,  1.5118])
tensor([0.0000, 1.5118])

3、两者的比较

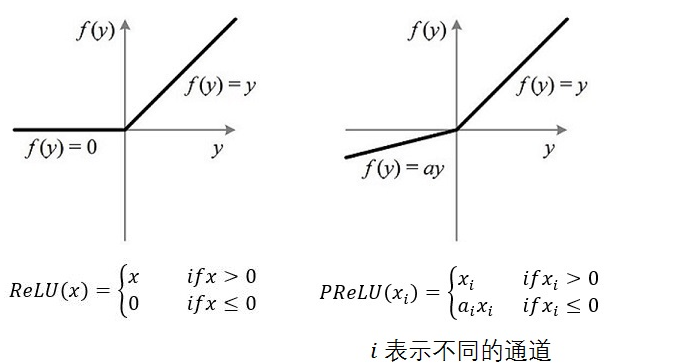
?4、总结

ReLU函数的计算是在卷积之后进行的，它和tanh函数和sigmoid函数一样，都属于非线性激活函数。ReLU函数的倒数在正数部分是恒等于1的，因此在深度网络中使用relu激活函数就不会导致梯度小和爆炸的问题。并且，ReLU函数计算速度快，加快了网络的训练。不过，如果梯度过大，导致很多负数，由于负数部分值为0，这些神经元将无法激活（可通过设置较小学习率来解决，对应PReLU中的可学习参数a）。