开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> SLAM_BA中重投影误差e 关于相机位姿扰动量δξ 的雅克比矩阵J 公式推导 -> 正文阅读

[人工智能]SLAM_BA中重投影误差e 关于相机位姿扰动量δξ 的雅克比矩阵J 公式推导

1. 推导的公式是什么

在SLAM中，为了使用重投影误差 e 对相机的位姿 ξ （李代表示形式）进行优化，需要求重投影误差e关于相机位姿扰动量δξ （本文使用左乘扰动，参考SLAM十四讲7.7.3节）的雅克比矩阵J?=?。该公式在代码中（如G2O中）进行相机位姿的优化求解。

结果如下，其中 $P' = [X',Y',Z']^T$ 表示相机坐标系下的三维坐标点。

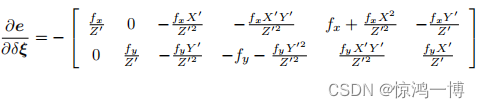
2. 推导过程

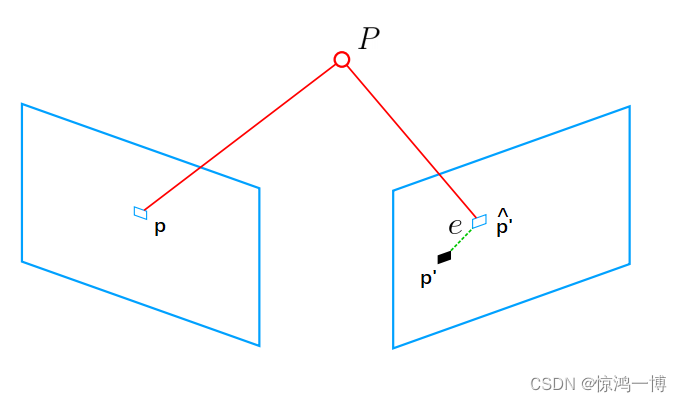
当我们知道了一个3D空间点坐标P (第i个点表示为 $Pi = [X_i , Y_i , Z_i]^T$ ）和其对应的2D图像坐标 p（上图左侧图像）时，我们可以根据相邻图像的图像特征找到在另一幅图中与之对应的图像点p'（上图右侧图像） (对于第i个点表示为? $p'_i= [u'_i, v'_i]^T$ )；假设我们知道右侧图像的相机位姿（或称相机外参矩阵，即相对于世界坐标系的变换矩阵）为?ξ（李代表示形式，6为向量，前三维代表平移，后三维代表旋转）则可以通过下式(作了齐次化变化)，将三维空间点P投影到右侧图像点上? $\hat{p'}$ =? $[\hat{u'_i}, \hat{v'_i}]^T$ ：

$s'_i \hat{p'}=s'_i\begin{bmatrix} \hat{u'_i}\\ \hat{v'_i}\\ 1 \end{bmatrix} = K exp(\xi^{\triangle} )\begin{bmatrix} X_i\\ Y_i\\ Z_i\\ 1 \end{bmatrix}$

其中 K表示相机的内参矩阵， $\xi^{\triangle}$ ?表示相机位姿向量（李代数表示形式）对应的反对称矩阵；设P' (记作 $P' = [X',Y',Z']^T$ ,第i个点对加下标i)为相机坐标系下的点坐标值，作为中间变量，则

$P' = exp(\xi^{\triangle} )\begin{bmatrix} X_i\\ Y_i\\ Z_i\\ 1 \end{bmatrix} = exp(\xi^{\triangle} )P = TP$ ，

其中，T表示相机的位姿，P表示空间点在世界坐标系下的坐标；所以，可表示为

? ? $\hat{p'} = \frac{1 }{?{s'_i}}KP'$

? $s'_i\begin{bmatrix} \hat{u'_i}\\ \hat{v'_i}\\ 1 \end{bmatrix} = \begin{bmatrix} f_x & 0 & c_x\\ 0 & f_y & c_y\\ 0& 0 & 1 \end{bmatrix} \begin{bmatrix} X'_i\\ Y'_i\\ Z'_i\end{bmatrix}$ ?

所以，可得

$\left\{\begin{matrix} \hat{u'_i} = f_x\frac{X'_i}{Z'_i}+c_x\\ \hat{v'_i} = f_x\frac{Y'_i}{Z_i'}+c_y \end{matrix}\right.$ ????????

则一个点的重投影误差? $e_i = p' - \hat{p'}$ ，可表示为

$e_i =p'_i - \frac{1 }{?{s'_i}}KP'$

即

$\large e = \left\{\begin{matrix} u = u'_i- f_x\frac{X'_i}{Z'_i}-c_x\\ v = v'_i - f_x\frac{Y'_i}{Z_i'}-c_y \end{matrix}\right.$ ?... （公式1）

构造最小二乘法时，求解的相机位姿? $\xi ^*$ 时，正是将该误差最小化，假设有n个这样的点对，则

$\xi ^* = arg \, \underset{\xi}{min}\frac{1}{2}\sum_{i=1}^{n}\left \| p'_i -\frac{1 }{?{s'_i}}KP'\right \|$

所以，对相机位姿? $\xi$ 左乘扰动量 $\delta \xi$ ，然后考虑? $e$ ?的变化关于扰动量 $\delta \xi$ 的导数。利用链式法则，可以列写如下：

根据（公式1）以及向量（e：2维）对向量（P'：3维）的求导法则，采用分子布局的形式（求导的结果矩阵的行数以分子为准）可得（不计下标i），

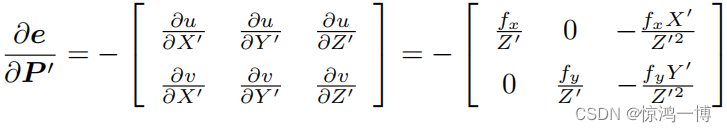
...... （公式2）

根据李代数的求导法则，相机的位姿T，乘以世界坐标系下点坐标P，对应相机扰动模型下 $\delta \xi$ 的导数公式（参考视觉SLAM十四讲公式4.3.5），可知：

$\frac{\partial (TP)}{\partial \delta \xi } = (TP)^{\bigodot} = \begin{bmatrix} I & -P'^{\wedge }\\ 0^T & 0^T \end{bmatrix}$

其中,I为3x3单位矩阵， $P'^{\wedge }$ 表示相机坐标系下的坐标对应的反对称矩阵。所以取出前三行得，

$\frac{\partial P'}{\partial \delta\xi } = \frac{\partial TP}{\partial \delta\xi }=[I, -P'^{\wedge }]$ ?...... （公式3）

所以，上述（公式2）乘以（公式3），可得，

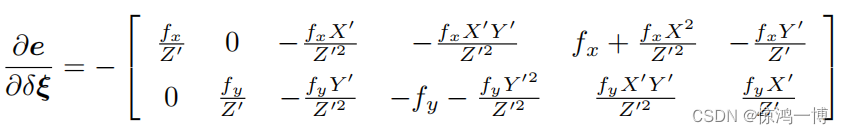
注意，G2O中，采用的相机位姿的李代表示是旋转在前，平移在后，所以是上式的后三列在前，前三列在后。?

3. G2O中代码实现（部分）

来源：g2o/types/sba/types_six_dof_expmap.cpp

void EdgeProjectXYZ2UV::linearizeOplus() {
  VertexSE3Expmap * vj = static_cast<VertexSE3Expmap *>(_vertices[1]);
  SE3Quat T(vj->estimate());
  VertexSBAPointXYZ* vi = static_cast<VertexSBAPointXYZ*>(_vertices[0]);
  Vector3D xyz = vi->estimate();
  Vector3D xyz_trans = T.map(xyz);

  double x = xyz_trans[0];
  double y = xyz_trans[1];
  double z = xyz_trans[2];
  double z_2 = z*z;

  const CameraParameters * cam = static_cast<const CameraParameters *>(parameter(0));

  Matrix<double,2,3,Eigen::ColMajor> tmp;
  tmp(0,0) = cam->focal_length;
  tmp(0,1) = 0;
  tmp(0,2) = -x/z*cam->focal_length;

  tmp(1,0) = 0;
  tmp(1,1) = cam->focal_length;
  tmp(1,2) = -y/z*cam->focal_length;

  _jacobianOplusXi =  -1./z * tmp * T.rotation().toRotationMatrix();

  _jacobianOplusXj(0,0) =  x*y/z_2 *cam->focal_length;
  _jacobianOplusXj(0,1) = -(1+(x*x/z_2)) *cam->focal_length;
  _jacobianOplusXj(0,2) = y/z *cam->focal_length;
  _jacobianOplusXj(0,3) = -1./z *cam->focal_length;
  _jacobianOplusXj(0,4) = 0;
  _jacobianOplusXj(0,5) = x/z_2 *cam->focal_length;

  _jacobianOplusXj(1,0) = (1+y*y/z_2) *cam->focal_length;
  _jacobianOplusXj(1,1) = -x*y/z_2 *cam->focal_length;
  _jacobianOplusXj(1,2) = -x/z *cam->focal_length;
  _jacobianOplusXj(1,3) = 0;
  _jacobianOplusXj(1,4) = -1./z *cam->focal_length;
  _jacobianOplusXj(1,5) = y/z_2 *cam->focal_length;
}