这次博客的主题是全景拼接,这个是建立在前面学过的特征提取、特征描述子、特征匹配等。
虽然图片是反应三维世界,但实质是二维的,因此图像拼接的可以简化理解为2D图像的变换、叠加过程。
图像之间经过特征匹配后的变换、叠加过程包括了位移、旋转、尺度、仿射、透视。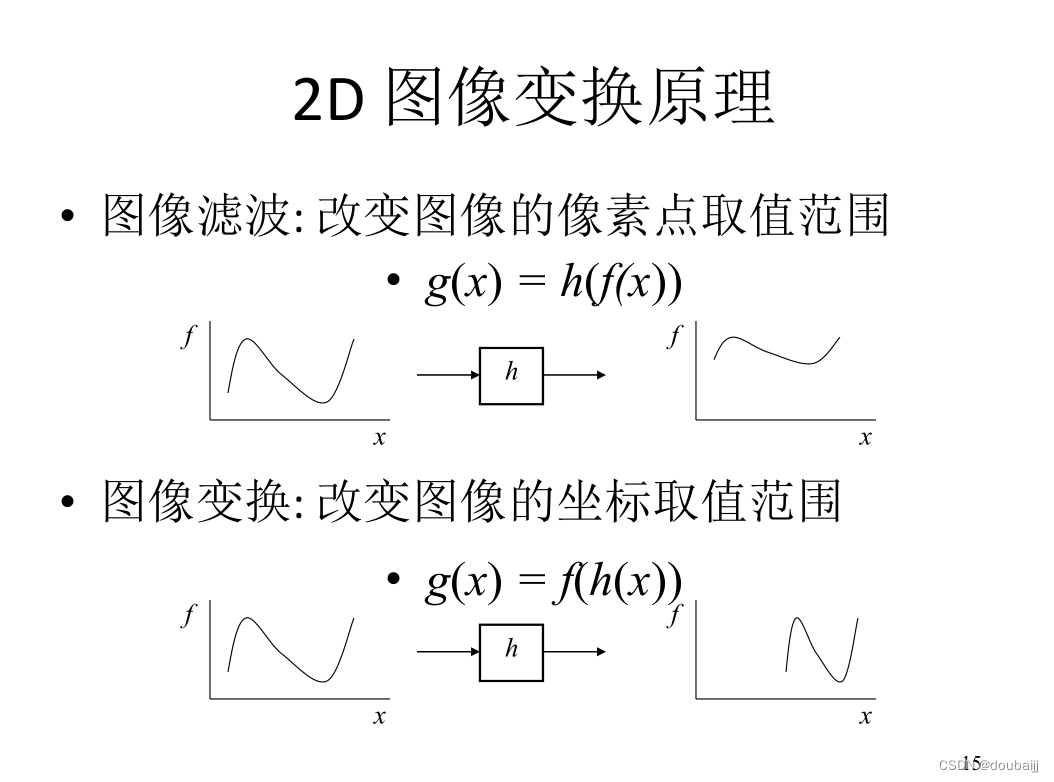
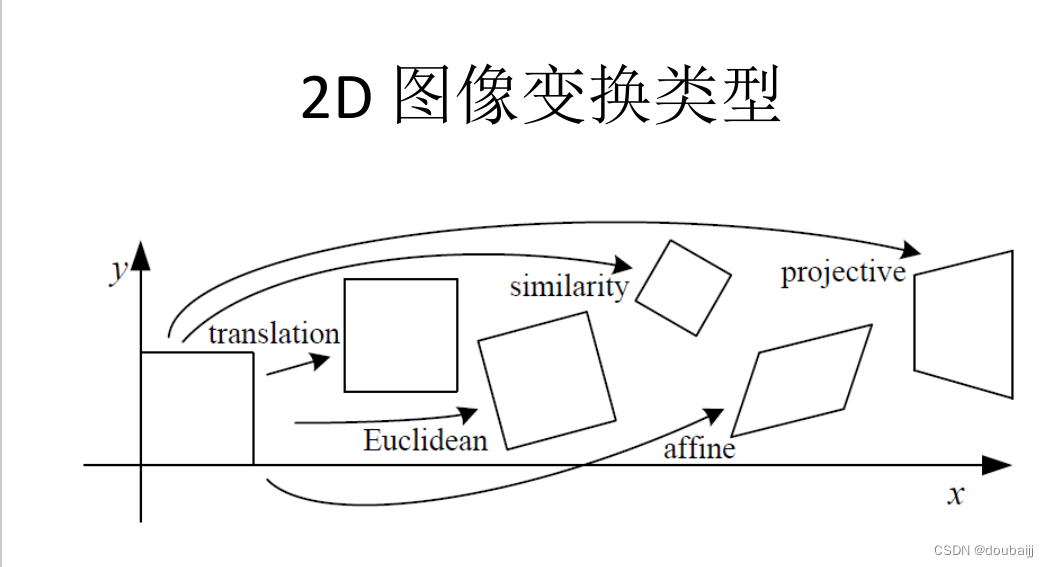
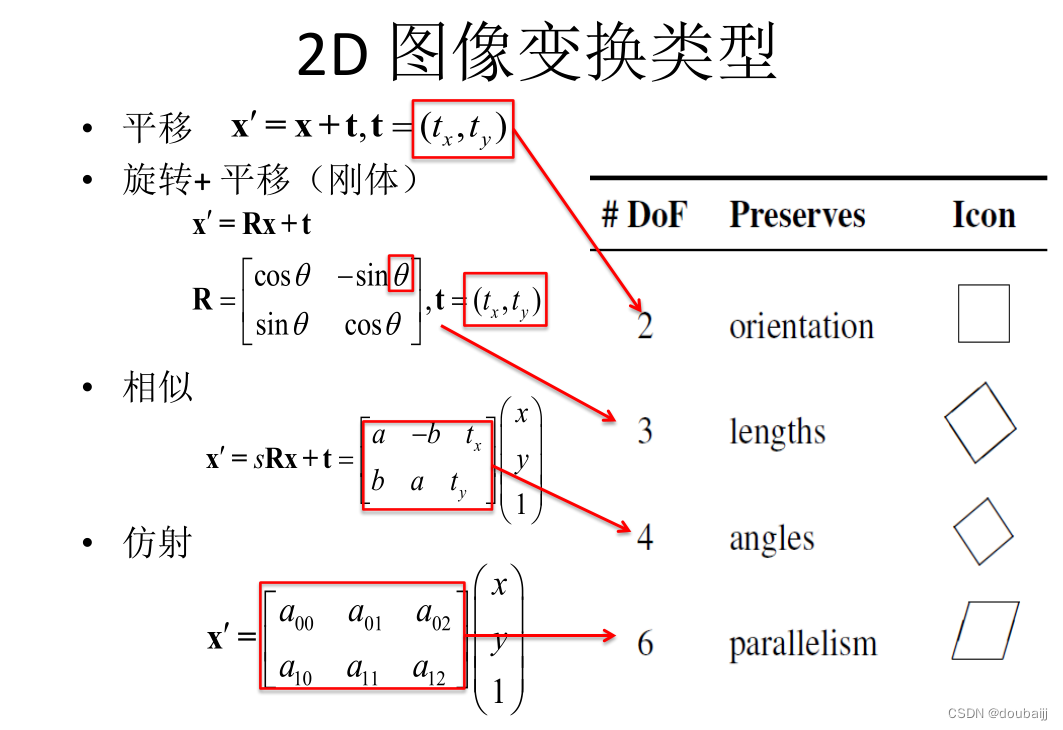
单应性变换
以上对图像的操作都涉及单应性变换,单应性变换是将一个平面内的点映射到另一个平面内的二维投影变换,对于平面中的点,用齐次坐标可以有效表示,即单应性变换矩阵H:
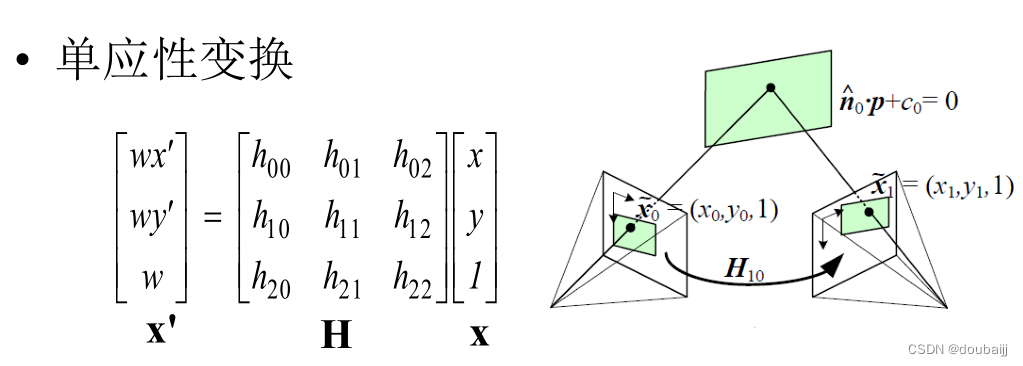
单应性矩阵仅依赖尺度定义,所以,单应性矩阵具有 8 个独立的自由度。我们通常使用 w=1 来归
一化点,这样,点就具有唯一的图像坐标 x 和 y。以上,我们就可以仅通过一个矩阵来进行图像的变换。
归一化和转换齐次坐标方程:
def normalize(points):
""" 在齐次坐标意义下,对点集进行归一化,使最后一行为 1 """
for row in points:
row /= points[-1]
return points
def make_homog(points):
""" 将点集(dim×n 的数组)转换为齐次坐标表示 """
return vstack((points,ones((1,points.shape[1])))) 直接线性变换
一个完全射影变换具有 8 个自由度。每个对应点对可以写出两个方程,分别对应于 x 和 y 坐标:比如平移存在两个未知数,仅需要一个点对。因此,计算单应性矩阵 H 需要4个对应点对。
将单应性矩阵 H 作用在对应点对上,可以得到 Ah=0,其中 A 是一个具有对应点对二倍数量行数的矩阵。将这些对应点对方程的系数堆叠到一个矩阵中,我们可以使用 SVD算法找到 H 的最小二乘解。
![]()
![]()
def H_from_points(fp,tp):
"""使用线性 DLT 方法,计算单应性矩阵 H,使 fp 映射到 tp。点自动进行归一化 """
if fp.shape != tp.shape:
raise RuntimeError('number of points do not match')
# 对点进行归一化(对数值计算很重要)
# --- 映射起始点 ---
m = mean(fp[:2], axis=1)
maxstd = max(std(fp[:2], axis=1)) + 1e-9
C1 = diag([1/maxstd, 1/maxstd, 1])
C1[0][2] = -m[0]/maxstd
C1[1][2] = -m[1]/maxstd
fp = dot(C1,fp)
# --to points--
m = mean(tp[:2], axis=1)
maxstd = max(std(tp[:2], axis=1)) + 1e-9
C2 = diag([1/maxstd, 1/maxstd, 1])
C2[0][2] = -m[0]/maxstd
C2[1][2] = -m[1]/maxstd
tp = dot(C2,tp)
# 创建用于线性方法的矩阵,对于每个对应对,在矩阵中会出现两行数值
nbr_correspondences = fp.shape[1]
A = zeros((2*nbr_correspondences,9))
for i in range(nbr_correspondences):
A[2*i] = [-fp[0][i],-fp[1][i],-1,0,0,0,
tp[0][i]*fp[0][i],tp[0][i]*fp[1][i],tp[0][i]]
A[2*i+1] = [0,0,0,-fp[0][i],-fp[1][i],-1,
tp[1][i]*fp[0][i],tp[1][i]*fp[1][i],tp[1][i]]
U,S,V = linalg.svd(A)
H = V[8].reshape((3,3))
# decondition
H = dot(linalg.inv(C2),dot(H,C1))
# normalize and return
return H / H[2,2]?上面这函数的第一步是检查点对对应的两个数组中点的数目是否相同,因为算法的稳定性取决于坐标的表示情况和部分数值计算的问题,所以要对这些点进行归一化操作,使其均值为 0,方差为 1。然后根据点对构造矩阵A,最小二乘解即为矩阵 SVD 分解后所得矩阵 V 的最后一行。该行经过变形后得到矩阵 H。然后对这个矩阵进行处理和归一化,返回输出。
仿射变换
由于仿射变换具有 6 个自由度,因此我们需要三个对应点对来估计矩阵 H。通过将最后两个元素设置为 0,即 h 7 =h 8 =0,仿射变换可以用上面的 DLT 算法估计得出,同样地,这些点也需要经过预处理和去处理化操作:
def Haffine_from_points(fp,tp):
""" 计算 H,仿射变换,使得 tp 是 fp 经过仿射变换 H 得到的 """
if fp.shape != tp.shape:
raise RuntimeError('number of points do not match')
# condition points
# --from points--
m = mean(fp[:2], axis=1)
maxstd = max(std(fp[:2], axis=1)) + 1e-9
C1 = diag([1/maxstd, 1/maxstd, 1])
C1[0][2] = -m[0]/maxstd
C1[1][2] = -m[1]/maxstd
fp_cond = dot(C1,fp)
# --to points--
m = mean(tp[:2], axis=1)
C2 = C1.copy() #两个点集,必须都进行相同的缩放
C2[0][2] = -m[0]/maxstd
C2[1][2] = -m[1]/maxstd
tp_cond = dot(C2,tp)
# # 因为归一化后点的均值为 0,所以平移量为 0
A = concatenate((fp_cond[:2],tp_cond[:2]), axis=0)
U,S,V = linalg.svd(A.T)
# create B and C matrices as Hartley-Zisserman (2:nd ed) p 130.
tmp = V[:2].T
B = tmp[:2]
C = tmp[2:4]
tmp2 = concatenate((dot(C,linalg.pinv(B)),zeros((2,1))), axis=1)
H = vstack((tmp2,[0,0,1]))
# decondition
H = dot(linalg.inv(C2),dot(H,C1))
return H / H[2,2]图像扭曲
对图像块应用仿射变换,我们将其称为仿射扭曲,扭曲操作可以使用SciPy 工具包中的 ndimage 包来简单完成。命令:
????????transformed_im = ndimage.affine_transform(im,A,b,size)
使用如上所示的一个线性变换 A 和一个平移向量 b 来对图像块应用仿射变换。选项参数 size 可以用来指定输出图像的大小。、
反射扭曲可以实现将图像或者图像的一部分放置在另一幅图像中,使得它们能够和指定的区域或者标记物对齐:
def image_in_image(im1,im2,tp):
""" Put im1 in im2 with an affine transformation
such that corners are as close to tp as possible.
tp are homogeneous and counter-clockwise from top left. """
# points to warp from
m,n = im1.shape[:2]
fp = array([[0,m,m,0],[0,0,n,n],[1,1,1,1]])
# compute affine transform and apply
H = homography.Haffine_from_points(tp,fp)
im1_t = ndimage.affine_transform(im1,H[:2,:2],
(H[0,2],H[1,2]),im2.shape[:2])
alpha = (im1_t > 0)
return (1-alpha)*im2 + alpha*im1_t测试:
im1 = array(Image.open('C:\Python\imgs\jm2.jpg').convert('L'))
im2 = array(Image.open('C:\Python\imgs\zm.jpg').convert('L'))
# set to points
tp = array([[120,260,260,120],[16,16,305,305],[1,1,1,1]])
#tp = array([[675,826,826,677],[55,52,281,277],[1,1,1,1]])
im3 = image_in_image(im1,im2,tp)
figure()
gray()
subplot(141)
axis('off')
imshow(im1)
subplot(142)
axis('off')
imshow(im2)
subplot(143)
axis('off')
imshow(im3)
im3 = Image.fromarray(im3)
if im3.mode == 'I' or im3.mode == 'RGBA':
im3 = im3.convert('RGB')
im3.save('C:\Python\imgs\img3.jpg')结果:

?标记物的坐标 tp 是用齐次坐标意义下的坐标表示的。
在具有很强透视效应的情况下,我们不可能使用同一个仿射变换将全部 4 个角点变换到它们的目标位置,那么可以将图像分成两个三角形,然后对它们分别进行扭曲图像操作。
def alpha_for_triangle(points,m,n):
""" 对于带有由 points 定义角点的三角形,创建大小为 (m,n) 的 alpha 图
(在归一化的齐次坐标意义下 """
alpha = zeros((m,n))
for i in range(min(points[0]),max(points[0])):
for j in range(min(points[1]),max(points[1])):
x = linalg.solve(points,[i,j,1])
if min(x) > 0: #all coefficients positive
alpha[i,j] = 1
return alpha
# set from points to corners of im1
m,n = im1.shape[:2]
fp = array([[0,m,m,0],[0,0,n,n],[1,1,1,1]])
# first triangle
tp2 = tp[:,:3]
fp2 = fp[:,:3]
# compute H
H = Haffine_from_points(tp2,fp2)
im1_t = ndimage.affine_transform(im1,H[:2,:2],
(H[0,2],H[1,2]),im2.shape[:2])
# alpha for triangle
alpha = alpha_for_triangle(tp2,im2.shape[0],im2.shape[1])
im3 = (1-alpha)*im2 + alpha*im1_t
# second triangle
tp2 = tp[:,[0,2,3]]
fp2 = fp[:,[0,2,3]]
# compute H
H = Haffine_from_points(tp2,fp2)
im1_t = ndimage.affine_transform(im1,H[:2,:2],
(H[0,2],H[1,2]),im2.shape[:2])
# alpha for triangle
alpha = alpha_for_triangle(tp2,im2.shape[0],im2.shape[1])
im4 = (1-alpha)*im3 + alpha*im1_t
subplot(144)
imshow(im4)
axis('off')
show()
im4 = Image.fromarray(im4)
if im4.mode == 'F' or im4.mode == 'RGBA':
im4 = im4.convert('RGB')
im4.save('C:\Python\imgs\img4.jpg')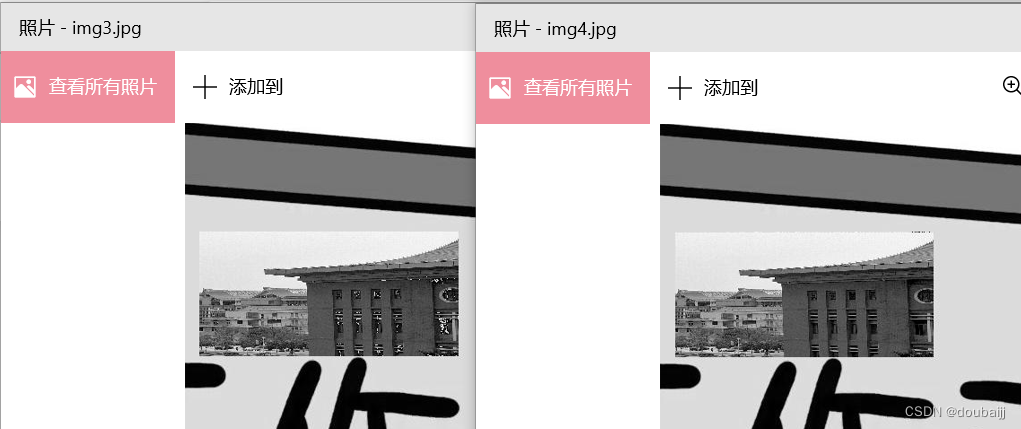
?以上三角形图像块的仿射扭曲可以完成角点的精确匹配。可以引出对应点对集合之间最常用的扭曲方式:分段仿射扭曲。给定任意图像的标记点,通过将这些点进行三角剖分,然后使用仿射扭曲来扭曲每个三角形,我们可以将图像和另一幅图像的对应标记点扭曲对应。
创建全景图
全景拼接时有出现鬼影现象,这是因为景深信息不同,那在面对参数求解过程中的从错误点对的干扰,比如给定若干二维空间中的点,求直线 y=ax+b ,使得该直线对空间点的拟合误差最小:
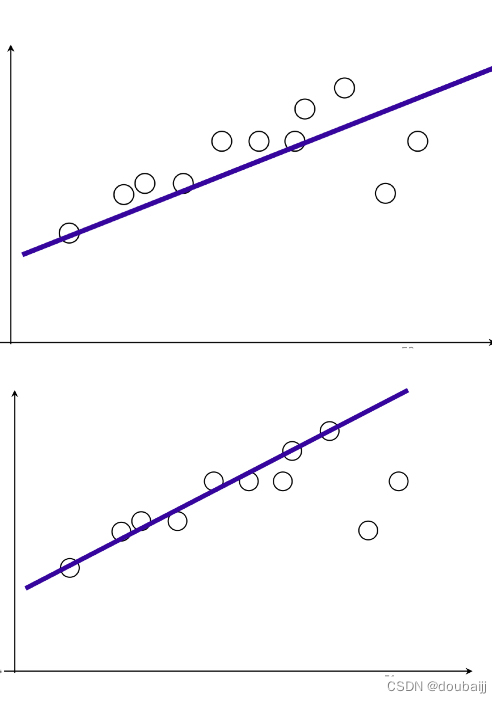
我们理想中的结果是下面那张图,但实际上最小二乘拟合出的直线是上面那张图,被噪声带跑了。RANSAC有效解决这一问题。
RANSAC(随机一致性采样)
没写好。。。。。
