图形解释

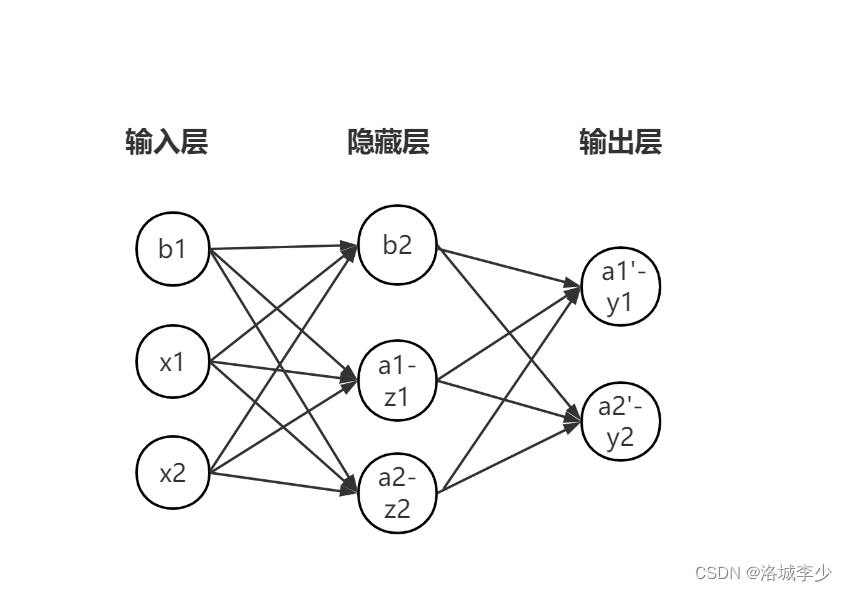
在这里插入图片描述
画图软件不太常用

代码实现

import numpy as np
def numerical_gradient(f,x):
    h=1e-4
    # 生成与x形状相同的数组
    grad=np.zeros_like(x)
    for idx in range(x.size):
        tmp_val=x[idx]
        x[idx]=tmp_val+h
        fxh1=f(x)
        x[idx]=tmp_val-h
        fxh2=f(x)
        grad[idx]=(fxh1-fxh2)/2*h
        x[idx]=tmp_val
    return grad
        
def sigmold(x):
    return 1/(1+np.exp(-x))
def softmax(a):
    c=np.max(a)
    exp_a=np.exp(a-c)
    sum_exp_a=np.sum(exp_a)
    y=exp_a/sum_exp_a
    return  y
def cross_enroty_errorly(y,t):
    if y.ndim==1:
        t=t.reshape(1,t.size)
        y=y.reshape(1,y.size)
    batch_size=y.shape(0)
    return -np.sum(np.log(y[np.arange(batch_size),t]+1e-7))/batch_size
class TwolayerNet:
    def __init__(self,input_size,hidden_size,output_size,weight_init_std=0.01):
        self.params={}
        self.params["w1"]=weight_init_std*np.random.randn(input_size,hidden_size)
        self.params["w2"]=weight_init_std*np.random.randn(hidden_size,output_size)
        self.params["b1"]=np.zeros(hidden_size)
        self.params["b2"]=np.zeros(output_size)
    def predict(self,x):
        w1,w2=self.params["w1"],self.params["w2"]
        b1,b2=self.params["b1"],self.params["b2"]
        a1 = np.dot(x,w1) + b1
        z1 = sigmold(a1)
        a2 = np.dot(z1,w2) + b1
        y=softmax(a2)
        return y
    def loss(self,x,t):
        y=self.predict(x)
        return cross_enroty_errorly(y,t)
    def accury(self,x,t):
        y=self.predict(x)
        y=np.argmax(y,axis=1)
        t=np.argmax(1,axis=1)
        accury=np.sum(y==t)/float(x.shape[0])
        return accury
    def numerical_gradient(self,x,t):
        loss_w=lambda w:self.loss(x,t)
        grads={}
        grads["w1"]=(loss_w,self.params["w1"])
        grads["b1"] = numerical_gradient(loss_w, self.params["b1"])
        grads["w2"] = numerical_gradient(loss_w, self.params["w2"])
        grads["b2"] = numerical_gradient(loss_w, self.params["b2"])
        return grads

内容解释

高数

两个常用函数

1.sigmoid

该函数实际上就是一个转换器，输入某个数会有值传出。
如h(2.0)=0.731
多用于二元分类问题

def sigmold(x):
    return 1/(1+np.exp(-x))

2.softmax
该函数负责完成信号的转换，输出的时概率，且输出的总和为1.
假设输出层有三个神经元，第一个神经元的输出y=该神经元的信号/三个输入信号之和

def softmax(a):
    c=np.max(a)
    exp_a=np.exp(a-c)
    sum_exp_a=np.sum(exp_a)
    y=exp_a/sum_exp_a
    return  y

mini-batch版交叉熵误差

y是神经网络的输出，t是监督数据
计算正确解标签的输出的自然对数

def cross_enroty_errorly(y,t):
    if y.ndim==1:
        t=t.reshape(1,t.size)
        y=y.reshape(1,y.size)
    batch_size=y.shape(0)
    return -np.sum(np.log(y[np.arange(batch_size),t]+1e-7))/batch_size

梯度

通过数值微分来确定梯度

def numerical_gradient(f,x):
    h=1e-4
    # 生成与x形状相同的数组
    grad=np.zeros_like(x)
    for idx in range(x.size):
        tmp_val=x[idx]
        x[idx]=tmp_val+h
        fxh1=f(x)
        x[idx]=tmp_val-h
        fxh2=f(x)
        grad[idx]=(fxh1-fxh2)/2*h
        x[idx]=tmp_val
    return grad