日常学习记录——决策树根节点的选择
1 数据集
本例使用的是经过预处理的模糊数据集,如下所示。其中,C1代表密度属性列,C2代表含糖量属性列,L、N、H分别代表偏低,中等,偏高这三个模糊语义。
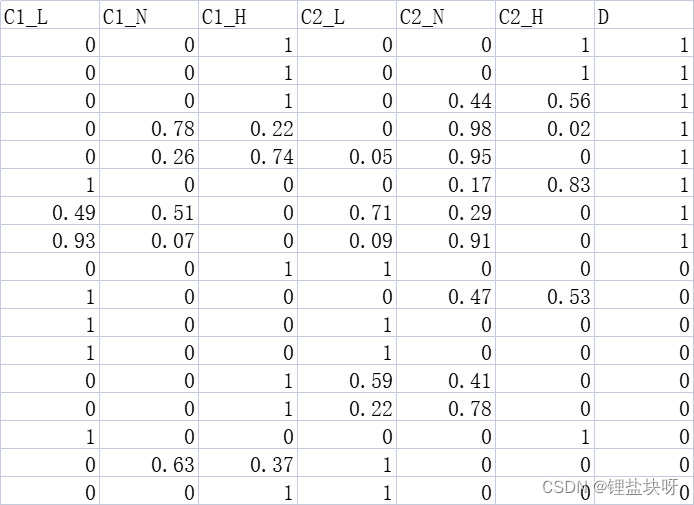
2 根节点的选择
1 信息增益的计算
代码如下:
# 计算数据集的信息熵
def cal_entD(target):
count_posi_label = 0
for i in range(len(target)):
if target[i] == 1:
count_posi_label = count_posi_label + 1
p1 = count_posi_label / len(target)
entD = -(p1 * math.log2(p1) + (1 - p1) * math.log2(1 - p1))
print(count_posi_label, len(target), p1, entD)
return entD
也就是完成西瓜书上的这一个过程: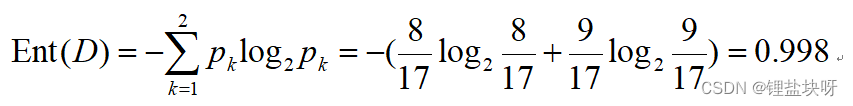
2 计算单列属性信息熵
代码如下:
# 计算单列属性的信息熵,如计算密度=密度_L时的信息熵
def cal_Ak(data, target, index):
count_Col = 0
count_posi_label = 0
for i in range(len(data)):
if data[i][index] != 0:
count_Col = count_Col + data[i][index]
if target[i] == 1:
count_posi_label = count_posi_label + 1 * data[i][index]
p1 = count_posi_label / count_Col
ent1 = -(p1 * math.log2(p1) + (1 - p1) * math.log2(1 - p1))
DV_D = count_Col / len(data)
DV_D_Ent = DV_D * ent1
return Bunch(
DV_D=DV_D,
Ent=ent1,
DV_D_Ent=DV_D_Ent
)
具体原理见西瓜书第76页。因为我用的是模糊化处理过的数据集,也不知道这么算是否是正确的,但是如果只数个数不考虑隶属度的问题的话,后面的信息增益会变小于0。所以这里分子选择对隶属度进行累加,分母选择了正例个数与隶属度取交集的算法。
3 计算各属性信息增益
代码如下:
# 计算密度的信息熵及信息增益
C1_l = cal_Ak(data, label, 0)
C1_n = cal_Ak(data, label, 1)
C1_h = cal_Ak(data, label, 2)
Gain_C1 = EntD - (C1_l.DV_D_Ent + C1_n.DV_D_Ent + C1_h.DV_D_Ent)
print(Gain_C1)
# 计算含糖量的信息熵及信息增益
C2_l = cal_Ak(data, label, 3)
C2_n = cal_Ak(data, label, 4)
C2_h = cal_Ak(data, label, 5)
Gain_C2 = EntD - (C2_l.DV_D_Ent + C2_n.DV_D_Ent + C2_h.DV_D_Ent)
print(Gain_C2)
运行结果如下,可见C2即含糖量的信息增益最大,所以根节点选择含糖量。

注释:
8:数据集包含正例个数 ,17:数据集总数,0.9975:数据集信息熵
0.03416:C1的信息增益
0.23947:C2的信息增益
3 存在问题与反思
虽然对根节点的选择有了一定的理解,但是后续的子节点的选择还是有点困难。目前分析可能有以下两个原因:
1、西瓜数据集强行采用模糊决策树的理论是不太合适的,因为在西瓜书上利用数据集3.0α做例子时,介绍了多变量决策树这一种分类方法。或许了解一下多变量决策树会更好一些。
2、其次,我可能太想构造一个模糊决策树出来了,但是单论模糊理论和决策树理论我都没有掌握的很好,还是要从底层出发,踏踏实实地学才可以。尤其是对模糊论集之间关系的理解与推理。
继续努力吧。
