????????前面介绍的线性回归与Softmax回归,都属于单层神经网络,而在深度学习领域,主要关注多层模型,这节主要熟悉多层感知机(MultiLayer Perceptron,MLP),因为神经网络是由感知机启发而来的,尤其是深度学习模型,都是很多层的。
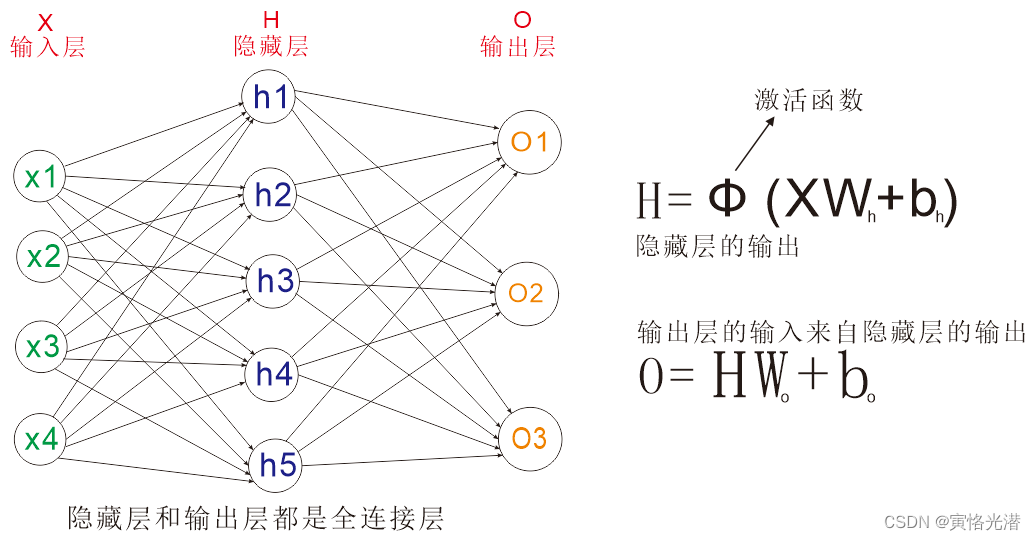
????????从图中我们可以看到,相比单层神经网络,多了一层隐藏层(Hidden Layer大于等于1),如果展开之后,我们发现其实本质上还是等价于一个单层神经网络,但是这个隐藏层的加入,可以解决很多非线性的问题,处理办法就是在每个隐藏层的每个神经单元加一个激活函数(逐元素操作),对于常见的激活函数的求导过程,有兴趣的可以查阅:sigmoid和tanh激活函数与其导数的绘图详解![]() https://blog.csdn.net/weixin_41896770/article/details/124425011
https://blog.csdn.net/weixin_41896770/article/details/124425011
?多层感知机的构建
import d2lzh as d2l
from mxnet import nd
from mxnet.gluon import loss as gloss
batch_size=200
train_iter,test_iter=d2l.load_data_fashion_mnist(batch_size)
num_inputs,num_outputs,num_hiddens=784,10,256 #图片形状是28x28,输出为10个类别,隐藏层单元个数256
W1=nd.random.normal(scale=0.01,shape=(num_inputs,num_hiddens))
b1=nd.zeros(num_hiddens)
W2=nd.random.normal(scale=0.01,shape=(num_hiddens,num_outputs))
b2=nd.zeros(num_outputs)
params=[W1,b1,W2,b2]
for param in params:
param.attach_grad()
#ReLU激活函数
def relu(X):
return nd.maximum(X,0)
#多层感知机模型
def net(X):
X=X.reshape((-1,num_inputs))
H=relu(nd.dot(X,W1)+b1)
return nd.dot(H,W2)+b2
loss=gloss.SoftmaxCrossEntropyLoss()
num_epochs,lr=5,0.5
d2l.train_ch3(net,train_iter,test_iter,loss,num_epochs,batch_size,params,lr)#训练跟softmax一样,使用同样方法epoch 1, loss 0.8012, train acc 0.703, test acc 0.819
epoch 2, loss 0.4749, train acc 0.823, test acc 0.839
epoch 3, loss 0.4096, train acc 0.850, test acc 0.855
epoch 4, loss 0.3833, train acc 0.858, test acc 0.873
epoch 5, loss 0.3702, train acc 0.864, test acc 0.871
????????当我将隐藏层的单元个数增大到1000,测试结果看到损失率降低的快很多,准确率好像变化不大;将单元个数减少到50个,测试结果的准确率相对降低一点,这个参数属于超参数,有时候需要自己试着去调节,因为影响因素很多,有样本数量,初始化值等影响
新增一个隐藏层【两个隐藏层】,且epochs增加为10:
batch_size=200
train_iter,test_iter=d2l.load_data_fashion_mnist(batch_size)
num_inputs,num_outputs,num_hiddens=784,10,256 #图片形状是28x28,输出为10个类别,隐藏层单元个数256
W1=nd.random.normal(scale=0.01,shape=(num_inputs,num_hiddens))
b1=nd.zeros(num_hiddens)
W2=nd.random.normal(scale=0.01,shape=(num_hiddens,num_hiddens))
b2=nd.zeros(num_hiddens)
W3=nd.random.normal(scale=0.01,shape=(num_hiddens,num_outputs))
b3=nd.zeros(num_outputs)
params=[W1,b1,W2,b2,W3,b3]
for param in params:
param.attach_grad()
#ReLU激活函数
def relu(X):
return nd.maximum(X,0)
#多层感知机模型
def net(X):
X=X.reshape((-1,num_inputs))
H1=relu(nd.dot(X,W1)+b1)
H2=relu(nd.dot(H1,W2)+b2)
return nd.dot(H2,W2)+b2
loss=gloss.SoftmaxCrossEntropyLoss()
num_epochs,lr=10,0.5
d2l.train_ch3(net,train_iter,test_iter,loss,num_epochs,batch_size,params,lr)#训练跟softmax一样,使用同样方法epoch 1, loss 1.9877, train acc 0.424, test acc 0.683
epoch 2, loss 0.6836, train acc 0.721, test acc 0.805
epoch 3, loss 0.5642, train acc 0.790, test acc 0.826
epoch 4, loss 0.4941, train acc 0.820, test acc 0.810
epoch 5, loss 0.4614, train acc 0.832, test acc 0.838
epoch 6, loss 0.4328, train acc 0.842, test acc 0.837
epoch 7, loss 0.4079, train acc 0.850, test acc 0.861
epoch 8, loss 0.4003, train acc 0.853, test acc 0.858
epoch 9, loss 0.3858, train acc 0.857, test acc 0.846
epoch 10, loss 0.3765, train acc 0.861, test acc 0.860
?另外需要注意的就是relu激活函数中的maximum函数与max函数的区别
x1=nd.array([1,9,2])
x2=nd.array([2,3,33])
nd.maximum(x1,x2)
[ 2. 9. 33.]#逐个元素比较,返回大的
而max是在指定的维度里面返回大的
x3=nd.array([[11,4,2],[3,8,13]])
nd.max(x3)#[13.]
nd.max(x3,0,keepdims=True)#[[11. 8. 13.]]
nd.max(x3,axis=1)#[11. 13.]
nd.max(x3,axis=1,keepdims=True)#[[11.],[13.]]Gluon的简洁实现
import d2lzh as d2l
from mxnet import gluon,init
from mxnet.gluon import loss as gloss,nn
net=nn.Sequential()
net.add(nn.Dense(256,activation='tanh'),nn.Dense(10))#添加一个激活函数为tanh的隐藏层,单元个数为256个
net.initialize(init.Normal(sigma=0.01))
batch_size=200
train_iter,test_iter=d2l.load_data_fashion_mnist(batch_size)
loss=gloss.SoftmaxCrossEntropyLoss()
trainer=gluon.Trainer(net.collect_params(),'sgd',{'learning_rate':0.5})
num_epochs=5
d2l.train_ch3(net,train_iter,test_iter,loss,num_epochs,batch_size,None,None,trainer)epoch 1, loss 0.7378, train acc 0.729, test acc 0.802
epoch 2, loss 0.5022, train acc 0.817, test acc 0.814
epoch 3, loss 0.4516, train acc 0.834, test acc 0.821
epoch 4, loss 0.4144, train acc 0.848, test acc 0.848
epoch 5, loss 0.3968, train acc 0.854, test acc 0.843
?修改为三个隐藏层:
net.add(nn.Dense(256,activation='relu'))
net.add(nn.Dense(128,activation='relu'))
net.add(nn.Dense(64,activation='relu'))
net.add(nn.Dense(10))
net.initialize(init.Normal(sigma=0.01))
print(net.collect_params())sequential11_ (
? Parameter dense26_weight (shape=(256, 0), dtype=float32)
? Parameter dense26_bias (shape=(256,), dtype=float32)
? Parameter dense27_weight (shape=(128, 0), dtype=float32)
? Parameter dense27_bias (shape=(128,), dtype=float32)
? Parameter dense28_weight (shape=(64, 0), dtype=float32)
? Parameter dense28_bias (shape=(64,), dtype=float32)
? Parameter dense29_weight (shape=(10, 0), dtype=float32)
? Parameter dense29_bias (shape=(10,), dtype=float32)
)
epoch 1, loss 2.1370, train acc 0.150, test acc 0.262
epoch 2, loss 1.0931, train acc 0.553, test acc 0.765
epoch 3, loss 0.6632, train acc 0.748, test acc 0.788
epoch 4, loss 0.5276, train acc 0.806, test acc 0.805
epoch 5, loss 0.4569, train acc 0.832, test acc 0.846
????????最后讲解下net.initialize(init.Normal(sigma=0.01))这个0.01标准差的正态分布,一般来说,模型的权重参数都是采用正态分布的随机初始化,而不是自己去指定同样的值,为什么呢?因为大家想想,如果参数值都一样,是不是在正向传播和反向传播当中的参数值都没有变化,梯度值也没有在迭代中优化,那么多层的神经网络跟单个隐藏层就没有区别了,所以我们都会对权重参数做随机初始化。
随机初始化除了正态分布,还有He和xavier,其中xavier的特点是不会受到输入层和输出层的个数的影响,Xavier公式为:? ? [其中a为输入个数,b为输出个数]
一般怎么选择,看激活函数,如果激活函数是ReLU就选择He,激活函数是sigmoid就选择Xavier.
