[人工智能]【自然语言处理】【知识图谱】SWCC：通过同时弱监督对比学习和聚类改善事件表示

论文地址：https://arxiv.53yu.com/pdf/2203.07633.pdf

一、简介

? 事件的分布式表示是一种常用的表示事件的方法，其能够为各种任务提供特征。但是，获得有效的事件表示是一项有挑战的任务。因此，需要分布式表示能够获得事件间的各种关系。两个事件可能会共享相同的事件属性(事件类型或者情感)，且两个事件可能存在因果关系或者时序关系。

? 早期的方法主要是利用事件的共现关系来学习事件的分布式表示。共享关系虽然很有用，但是对于深入的理解事件来说还是太粗糙。近期的工作则是尝试使用细粒度的知识，例如：语言关系和常识知识。具体来说，$\text{Lee}$等人利用11个语言关系类型来建模事件知识，而$\text{Ding}$等人则将人工标注的常识合并至事件表示中。然而，细粒度知识太过多样，而目前的细粒度知识仅是事件知识的一小部分。此外，人工标注的知识非常昂贵且无法扩展到大规模数据集上。

? 在本文的工作中，作者观察到共享事件中存在着非常丰富的信息，但是先前的研究被没有很好的利用这些信息。基于现有的实际关系抽取研究，共现关系(指两个事件在同一文档中出现)能够被看作是精确语言关系的超集。具体来说，这些关系能够通过语言中的标记来表示，例如：$\text{because}$能够捕获因果关系。此外，共现关系也包含了其他隐含的事件知识，例如：相同文档中的事件可能共享相同的主题和事件类型。先前的工作为例学习基于共现信息的事件表示，通常会利用$\text{margin?loss}$来进行实例级对比学习，该loss由一个anchor、正样本和负样本组成。但是，该loss有两个局限性：(1) 由于$\text{margin?loss}$中的每个anchor仅考虑一个正样本和一个负样本，因此在捕获不同语义事件上表现的十分挣扎；(2) 随机采样的负样本可能包含与anchor语义相关的样本。

? 本文的动机是解决上面的问题，并更好的利用事件的共现信息。因此，本文提出了$\text{SWCC}$：一个同时进行弱监督对比学习和聚类的事件表示学习框架。为了解决第一个问题，使用$\text{InfoNCE}$目标函数来构建对比学习框架，其使用一个正样本和多个负样本。此外，本文还将$\text{InfoNCE}$扩展至弱监督对比学习中，并且允许对每个anchor考虑多个正样本和多个负样本。共现事件也被作为额外的正样本，并使用共现频率作为权重。为了解决第二个问题，本文还引入了一个基于prototype的聚类方法来避免语义相关的事件被拉远。

? 总的来说，本文的贡献如下：

• 提出了一个简单且有效的事件表示学习框架$\text{SWCC}$，其能够更好的利用事件的共现信息来学习事件表示；

• 引入了一个弱监督对比学习方法，允许同时考虑多个正例和多个负例，并提出一个基于prototype的聚类方法来避免语义相关的事件被拉远；

• 针对基于prototype的聚类方法提供了全面的分析，并且发现学习到的prototype向量潜在包含着事件的各种关系；

二、相关技术

1. 事件表示模型

? 在早期，$\text{Neural?Tensor?Networks(NTNs)}$被广泛的用来构成事件组件的向量表示，即$\text{(subject,predicate,object)}$。但是，这种方法引入了很强的组合归纳偏差，并且不能扩展至具有更多论元的事件。近期的研究工作尝试使用预训练语言模型来替换静态词向量，从而获得效果更好的事件表示。本文同样也使用$\text{BERT}$作为backbone模型。

? $\text{BERT}$编码器将文本作为输入，输入的形式如下：

$$\text{[CLS]},pred,subj,obj,[SEP]\text{\hspace{1em}(1)}$$
定义$\text{x}=[x_0,x_1,\dots ,x_L]$是长度为$L$的输入序列，其中$x_0$和$x_L$是$\text{[CLS]}$的token和$\text{[SEP]}$的token。给定$\text{x}$，$\text{BERT}$返回一个上下文向量序列
$$[{\text{v}}_{\text{[CLS]}},{\text{v}}_{x_1},\dots ,{\text{v}}_{x_L}]=\text{BERT}(\text{x})\text{\hspace{1em}(2)}$$
其中，${\text{v}}_{\text{[CLS]}}$是token $\text{[CLS]}$的向量表示。事件最终的向量表示$\text{z}$是输出的$\text{[CLS]}$的向量表示：$\text{z}={\text{v}}_{\text{[CLS]}}$。

2. 实例级对比学习

? 通过对比学习来训练事件表示模型。对比学习的目标是将相关的事件拉近并将不相关的事件拉远。$\text{margin?loss}$在许多事件表示学习工作中被广泛的使用。最近提出的对比损失函数$\text{InfoNCE}$在各种对比学习任务中展现了其有效性。$\text{Chen}$等人进一步证明了$\text{InfoNCE}$比$\text{margin?loss}$更好。因此，本文使用$\text{InfoNCE}$来训练事件表示模型。

? 正式来说，给定一个由$N$对事件构造的数据集 D = { x i , x i + } i = 1 N \mathcal{D}=\{\textbf{x}_i,\textbf{x}_i^+\}_{i=1}^N D={xi?,xi+?}i=1N?，其中其中${\text{x}}_i^{+}$是${\text{x}}_i$的正样本。$\text{InfoNCE}$在样本对$({\text{x}}_i,{\text{x}}_i^{+})$上的计算方式为
$$\mathcal{L}=?\text{log}\frac{g({\text{z}}_i,{\text{z}}_i^{+})}{g({\text{z}}_i,{\text{z}}_i^{+})+{\sum }_{k\in \mathcal{N}(i)}g({\text{z}}_i,{\text{z}}_k)}\text{\hspace{1em}(3)}$$
其中，${\text{z}}_i$和${\text{z}}_i^{+}$是样本${\text{x}}_i$和${\text{x}}_i^{+}$的增强表示，$k\in \mathcal{N}(i)$是batch内负样本的索引，$g$是一个相似度度量函数$g({\text{z}}_i,{\text{z}}_k)=\text{exp}({\text{z}}_i^{?}{\text{z}}_k/\tau )$，其中$\tau \in {\mathbb{R}}^{+}$是一个temperature值。

3. 数据增强

? 对比学习中的关键问题是如何获取${\text{z}}_i^{+}$。在自然语言中，${\text{z}}_i^{+}$通过是先对${\text{x}}_i$进行词删除、重排和替换来实现数据增强，然后将增强的数据输入至表示模型中获得。近期的一些工作利用$\text{dropout}$噪音实现自然语言上的数据增强，并且发现这种增强技术的表现要好于常见的数据增强技术。具体来说，给定一个事件${\text{x}}_i$，将该事件输入$\text{BERT}$编码器两次，从而获得两个向量表示${\text{z}}_i$和${\text{z}}_i^{+}$，两次的不同在于不同的$\text{dropout?mask}$：
$${\text{z}}_i=f_{\theta }({\text{x}}_i,{?}_1),{\text{z}}_i^{+}=f_{\theta }({\text{x}}_i,{?}_2)\text{\hspace{1em}(4)}$$
其中，${?}_1$和${?}_2$是两个不同的随机$\text{dropout?mask}$。

三、事件表示框架$\text{SWCC}$

?

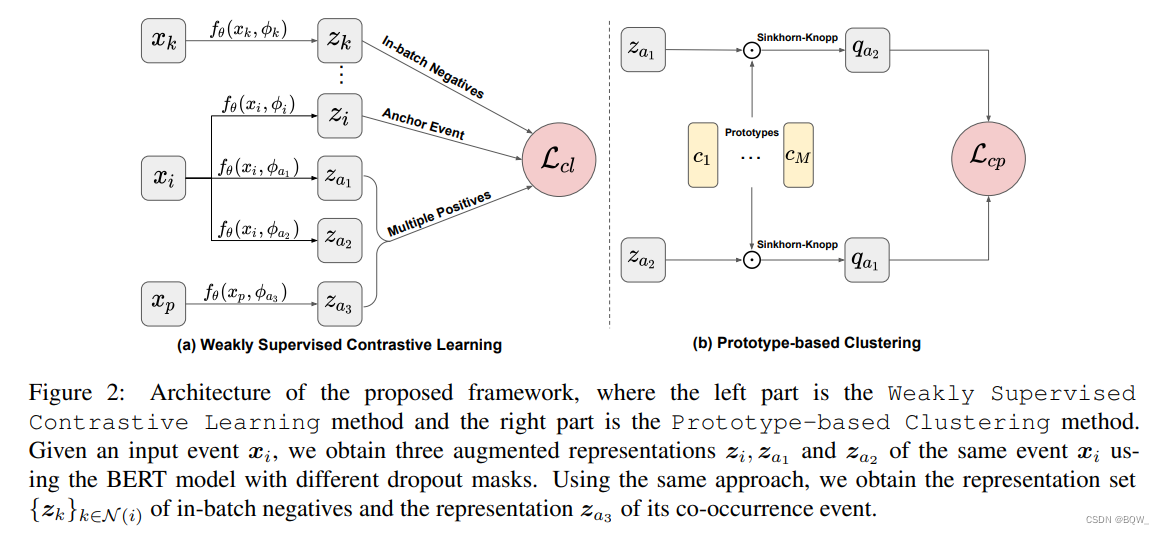
? 本小节将介绍框架的细节。上图展示了框架$\text{SWCC}$，其包含两部分：左边的弱监督对比学习方法和右边基于prototype的聚类方法。

1. 弱监督对比学习

? 这里使用基于$\text{InfoNCE}$损失函数来构建对比学习框架，而不是使用$\text{margin?loss}$。为了能够将共现的信息合并至事件表示，可以考虑将每个样本的共享事件作为额外的正样本，即$x_i $的正增强样本来自它的共现事件$x_p$。然而，原始的$\text{InfoNCE}$损失函数并不能处理多个正样本的情况。本文采用$\text{InfoNCE}$的变体，并引入了基于共享频率的加权机制。

1.1 共现作为弱监督

? 每个输入样本对表示为$(x_i,x_p)$，其中$x_i$和$x_p$指向输入事件和它的一个共现事件。首先，通过上面提到的事件表示模型为$x_i$计算一个增强表示，作为anchor事件。本方法与$\text{InfoNCE}$的不同在于构建$x_i$的正样本集合$\mathcal{A}(i)$。在$\text{InfoNCE}$中，$\mathcal{A}(i)$仅包含一个正样本。本文提出的方法中，通过推广等式$(3)$来支持多个正样本的学习
$$\mathcal{L}=\sum _{a\in \mathcal{A}(i)}?\text{log}\frac{g({\text{z}}_i,{\text{z}}_a)}{g({\text{z}}_i,{\text{z}}_a)+{\sum }_{k\in \mathcal{N}(i)}g({\text{z}}_i,{\text{z}}_k)}\text{\hspace{1em}(5)}$$
其中$\mathcal{A}(i)$和$\mathcal{N}(i)$指事件$x_i$的正样本集合和负样本集合。该损失函数支持任意数量的正样本，但考虑到$\text{GPU}$显存的限制，使用 A ( i ) = { z a 1 , z a 2 , z a 3 } \mathcal{A}(i)=\{\textbf{z}_{a1},\textbf{z}_{a2},\textbf{z}_{a_3}\} A(i)={za1?,za2?,za3??}，其中${\text{z}}_{a1}$和${\text{z}}_{a2}$是通过dropout获得事件$x_i$的两个增强表示，${\text{z}}_{a3}$则是一个共现事件的增强表示。${\text{z}}_{a_1}$和${\text{z}}_{a2}$将会被用于基于prototype的聚类方法。

1.2 合并共现频率

? 事件的共现频率表示链接的强度。为了更好的利用数据引入了权重机制，将事件间的共现频率作为实例权重来重写等式$(5)$
$${\mathcal{L}}_{cl}=\sum _{a\in \mathcal{A}(i)}?\text{log}\frac{{\epsilon }_a?g({\text{z}}_i,{\text{z}}_a)}{g({\text{z}}_i,{\text{z}}_a)+{\sum }_{k\in \mathcal{N}(i)}g({\text{z}}_i,{\text{z}}_k)}\text{\hspace{1em}(6)}$$
其${\epsilon }_a$是正样本${\text{z}}_a$的权重。正样本${\text{z}}_{a1}$和${\text{z}}_{a2}$的权重${\epsilon }_{a1}$和${\epsilon }_{a2}$被设置为${\epsilon }_{a1}={\epsilon }_{a2}=\frac{1}{|\mathcal{A}(i)|?1}$。共现事件${\text{z}}_{a3}$的权重${\epsilon }_{a3}$则需要先计算一个共现矩阵$\text{V}$，每个值对应两个事件的共现频率。使用$\text{Min-Max}$规范化方法将$\text{V}$规范化为$\hat{\text{V}}$，并使用$\hat{\text{V}}$中的取值作为共现事件的权重${\epsilon }_{a3}$。

2. 基于Prototype的聚类

? 为了避免语义关联的事件被拉开，引入了基于prototype的聚类方法。这里的prototype是一组语义相关事件的代表性向量表。在聚类的同时，强制一个实体的不同增强表示的簇分配保持一致。不同于实例级对比学习，本文的聚类方法通过事件表示和簇表示间的对比来使模型专注簇基本的语义。

2.1 簇预测

? 本方法使用簇分配作为中介来比较相同事件的不同增强表示。这种方法的动机是，若两个增强表示能够捕获相同的信息，那么就能从一个增强表示来预测另一个增强表示的簇分配。具体来说，给定$M$个prototype，每个prototype对应一个可学习向量${\text{c}}_i,i\in [M]$。给定一个输入事件，使用不同的dropout获得两个不同的增强表示，即事件${\text{x}}_i$的两个增强表示${\text{z}}_{a1}$和${\text{z}}_{a2}$。计算这两个增强表示与$M$个prototype的相似度，得到簇分配${\text{q}}_{a1}$和${\text{q}}_{a2}$。然后，交换两个增强样本的簇分配，并使用增强表示${\text{z}}_{a1}$预测簇分配${\text{q}}_{a2}$，且用${\text{z}}_{a2}$预测${\text{q}}_{a1}$。正式来说，簇预测损失函数为
$${\mathcal{L}}_{cp}=l(z_{a1},{\text{q}}_{a2})+l(z_{a2},{\text{q}}_{a1})\text{\hspace{1em}(7)}$$
其中，函数$l(\text{z,q})=?\text{q}\text{log}\text{p}$用来衡量表示$\text{z}$和簇分配$\text{q}$的拟合程度。$\text{p}$是$M$个prototypes的概率向量
$$p^{(j)}=\frac{\text{exp}({\text{z}}^{?}{\text{c}}_j/\tau )}{{\sum }_{k=1}^M\text{exp}({\text{z}}^{?}{\text{c}}_k/\tau )}\text{\hspace{1em}(8)}$$
其中，$\tau$是temperature超参数。直觉上，簇预测方法通过中间的簇分配${\text{q}}_{a1}$和${\text{q}}_{a2}$来链接表示${\text{z}}_{a1}$和${\text{z}}_{a2}$。

2.2 计算簇分配

? 这里使用"最优运输求解器"来计算簇分配，这个求解器能够确保所有增强表示被均等划分至簇。特别地，利用$\text{Sinkhorn-Knopp}$算法来求解最优运输问题。该算法开始于每个元素被初始化为${\text{z}}_b^{?}{\text{c}}_m$的矩阵$\Gamma \in {\mathbb{R}}^{M\times N}$，其中$b\in [N]$是每列的索引。然后迭代生成一个双标准化矩阵。

3. 模型训练

? $\text{SWCC}$通过同时执行弱监督对比学习和基于prototype的聚类来学习事件表示。整个训练的损失函数有3项：
$${\mathcal{L}}_{overall}={\mathcal{L}}_{cl}+\beta {\mathcal{L}}_{cp}+\gamma {\mathcal{L}}_{mlm}\text{\hspace{1em}(9)}$$
其中，$\beta$和$\gamma$是超参数。

? 第一项是弱监督对比学习损失函数，其允许模型将共现信息合并至事件表示中。第二项是基于prototype的聚类损失函数，其强制同一输入事件的不同增强版本在簇分配上保持一致。最后一项是$\text{MLM}$目标损失函数，用于避免模型遗忘token级别的知识。

四、总结

• 通过聚类的方式来缓解对比学习导致的相似样本被拉远；
• 聚类能够使事件表示蕴含各种关系；

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖