[人工智能]Link Prediction Based on Graph Neural Networks

摘要

链接预测是网络结构化数据的一个关键问题。链路预测启发式方法使用一些得分函数，如共同邻居和Katz指数等来衡量链路的可能性。由于它们的简单性、可解释性，以及对其中一些启发式方法的可扩展性，因此获得了广泛的实际应用。然而，每一种启发式都有一个很强的假设，即两个节点何时有可能链接，这导致了它们在这些假设失效时的网络上链路预测的效果不好。在这方面，更合理的方法应该是从给定网络中学习一个合适的启发式，而不是使用预定义的启发式。通过提取每个目标链路周围的局部子图，我们的目的是学习一个将子图模式映射到链路存在的函数，从而自动学习一个适合当前网络的 “启发式”。在本文中，我们研究了这种用于链接预测的启发式学习范式。
首先，我们提出了一种新颖的γ-衰变启发式理论。该理论将各种启发式学习统一到一个框架中，并证明所有这些启发式学习都可以从局部子图中很好地逼近。我们的结果表明，局部子图保留了与链路存在相关的丰富信息。其次，基于γ-衰变理论，我们提出了一种新的方法，利用图神经网络（GNN）从局部子图学习启发式。其实验结果显示出了前所未有的性能，在多种问题上都能稳定地工作。

介绍

链接预测就是预测网络中的两个节点是否有可能存在链接。一些简单而有效的链接预测方法被称为启发式方法，例如共同邻居、Katz等，这些方法使用预设的假设来预测节点之间的链路。因此一旦假设失效，预测效果也会变差。
启发式算法并非是指某一个或者某几个, 而是某一些简单有效的预测方法
存在的问题: 以往启发式方法是假设具有很多共同邻居的两个节点,更有可能连接, 这个方法在社交领域是有效的, 但是在蛋白质相互作用中, 具有共同邻居的两个蛋白质很可能并没有相互作用
启发式算法学习到的是图中可以被观察到的节点和网络边缘结构内的特征, 这些特征可以直接从图中计算出来, 这些特征也被称为图结构特征
第一个提出的是 Zhang和Chen基于启发式算法可以被视为预训练的图结构特征, 提出了一个WLMN(神经机)的模型, 这个模型通过提取链接周围的局部封闭子图来作为训练数据, 使用一个全连接的神经网络去学习哪些封闭子图对应的链接是相通的, 并且提出的模型在链接预测上面效果很好
论文链接 Weisfeiler-Lehman Neural Machine for Link Prediction
封闭子图由一对节点 (x, y) 以及其 h 跳的邻居节点组成, 一跳封闭子图只包含x,y的直接邻居, 二跳包含是x,y的邻居节点 和 邻居的邻居节点, 以此类推, 这些封闭子图可以为链接预测提供丰富的信息, 所有的一阶启发式算法可以从封闭子图中计算出来
有研究表明 : 高阶启发式算法的性能要优于低阶启发式算法, 为了学习高阶特征, 我们需要一个非常大的跳数去构建封闭子图. 但是跳数h越高的网络在训练时需要消耗大量的内存资源与时间, 然而本文提出了一个疑问 :
是否真的有必要那么大的跳数来学习高阶启发式算法吗?
本文中, 通过研究链接预测的内在机制, 发现通过伽马衰减理论可以对大多数的高阶启发式进行统一.
创新点 : 基于伽马衰减理论, 使用一个小的h跳的子图去逼近高跳子图, 以此来使用低跳的子图去学习高阶启发式的特征.

本文的贡献 :
● 提出了一个学习链接预测的新理论启发式学习的新理论，证明了从局部子图而不是整个网络学习的合理性
● 提出了SEAL。一个基于GNN的新型链接预测框架（如上图所示）。SEAL优于所有启发式方法、潜在特征方法和最近的网络嵌入方法都有很大优势。SEAL也优于之前最先进的方法WLNM。

准备工作 :
符号定义
…

潜在特征和隐式特征

本文除了图结构特征外，还研究了潜在特征和显式特征以进行链接预测。潜在特征方法通过分解网络的一些矩阵表示，以学习每个节点的低维潜在表示/嵌入。示例包括矩阵分解[3]和随机块模型[18]等。最近，已经提出了许多网络嵌入技术，例如DeepWalk [19]、LINE [21]和node2vec [20]，它们也是潜在特征方法，因为它们也隐含地分解了一些矩阵[22]。显式特征通常以节点属性的形式提供，描述有关各个节点的各种辅助信息。结果表明，将图结构特征与潜在特征和显式特征相结合可以提高性能

统一的链接预测的启发式方法

在这个篇章, 主要是介绍链接预测启发式背后的各种机制, 并且由于已有的大量图学习技术, 所以本篇并不去关心某一个特定方法的泛化误差, 而是主要把重点关注在抽取出来的子图中的启发式方法的信息。
封闭子图的定义 :

定义一个图为 : $G=(V,E)$ 给定两个节点 $x,y\in V$
对应的 h 跳的子图$G_{x,y}^h$ 是从图 $G$所推导出的节点集: { i ∣ d ( i , x ) ≤ h ?or? d ( i , y ) ≤ h } \{i \mid d(i, x) \leq h \text { or } d(i, y) \leq h\} {i∣d(i,x)≤h?or?d(i,y)≤h}
定义1
任何 $(x,y)$的 h 跳 启发式都可以从 $G_{x,y}^h$精确的计算
例如，一个2跳的包围子图将包含计算任何一阶和二阶启发法所需的所有信息。但是，尽管一阶和二阶启发式方法被局部包围子图很好地覆盖，但对于学习高阶启发式方法来说，似乎仍然需要一个非常大的h阶启发式方法。令人惊讶的是，我们下面的分析表明，学习高阶启发式方法在小的h下也是可行的。
我们首先通过定义γ递减启发式来支持这一点。我们将表明在某些条件下，γ递减启发式可以很好地从 h-hop
包围的子图。此外，我们还将证明，几乎所有著名的高阶启发式方法都可以统一到这个γ递减启发式的框架中。

定义1: 伽马衰减启发式

$(x,y)$的 $\gamma$ 衰减启发式具有以下的形式 :
KaTeX parse error: No such environment: equation at position 7: \begin{?e?q?u?a?t?i?o?n?}? \mathcal{H}(x,…

上述公式中$\gamma$是介于0到1之间的衰减因子, $\eta$是 $\gamma$的一个正常数或者正函数, 其上界是一个常数
接下来，我们将证明在一定条件下，一个$\gamma$衰减启发式可以从一个h跳包围子图中近似，并且近似误差至少随h呈指数减小。

定理2
给定一个$\gamma$衰减启发式 $\mathcal{H}(x,y)=\eta {\sum }_{l=1}^{\infty }{\gamma }^{l}f(x,y,l)$ 如果 $f(x,y,l)$满足 :

然后 H(x,y) 就可以从 $G_{x,y}^h$中近似得到, 并且近似误差随着 h 的增加随着指数级减少

证明部分 :

SEAL : 基于GNN的理论实现

在本章节主要是介绍SEAL框架, SEAL框架主要是学习图结构的一般特征进行链接预测.
步骤如下 :
● 提取封闭子图
● 构造节点信息矩阵
● GNN学习

给定一个网络, 目标是可以自动的学习一个能够最好解释链接形成的启发式函数, 受到理论结果的启发, 该函数将链接周围的封闭子图作为输入, 并输出一个链接存在的可能性. 为了学习这样的一个函数, 我们在封闭子图上训练一个图神经网络。
SEAL的第一步是 : 提取一组采样的可以被观察到的正链接 和 不可被观察到的负链接的封闭子图来构造训练数据。GNN通常是以 $(A,X)$ 作为输入, 其中 $A$是作为输入子图的邻接矩阵, $X$是封闭子图的节点信息矩阵, 每一行是对应一个节点的特征向量。
SEAL的第二步是 : 为每个封闭子图构造节点信息矩阵 $X$ ,这一步对于训练一个成功的 GNN链接预测模型相当重要, 下面会继续讨论这个步骤, 另外 SEAL中的节点信息矩阵 $X$由三部分组成 : 结构节点标签、节点嵌入 和 节点属性。

结构节点标签

节点信息矩阵 $X$的第一个部分是每个节点的结构标签, 节点标签函数 : $f(x):V\to N$ 封闭子图中的每一个节点 $i$都会被分配一个整数标签$f(i)$, 目的是为了使用不同的标签来标记节点在封闭子图中的不同的角色。

1. 中心节点x和y是链接所在的目标节点
2. 与中心节点有不同相对位置的节点
   与中心节点的相对位置不同的节点对链接结构重要性也不同, 一个适当的节点应该标记出这些差异, 否则GNN无法预测目标节点之间是否链接, 且丢失结构信息。
   节点的标记方法标准如下 :
3. 目标节点 x 和 目标节点y 的标签不能有相同的标签
4. 一个节点 $i$ 在一个封闭的子图中的拓扑位置可以用它相对于两个中心节点的半径来描述, 即 : $(d(i,x),d(i,y))$
   因此, 我们让相同的轨道上的节点具有相同的标签, 这样节点的标签就可以反应节点在子图中的相对位置和结构重要性.
   基于上述标准，我们提出如下的双半径节点标记（DRNL）。首先，将标签 1 分配给 x 和 y。然后，对于任何具有 $(d(i,x),d(i,y))=(1,1)$的节点 i，分配标签 $(f_l(i)=2)$。半径为 (1, 2) 或 (2, 1) 得到标签 3. 半径为 (1, 3) 或 (3, 1) 的节点得到 4. 具有 (2, 2) 的节点得到 5. 具有 (1, 4) 或 (4, 1) 的节点得到 6. 节点用 (2, 3) 或 (3, 2) 得到 7。以此类推。换句话说，我们迭代地将更大的标签分配给具有更大半径 w.r.t 的节点。两个中心节点，其中标签 $f_l(i)$和双半径 $(d(i,x),d(i,y))$ 满足

结合潜在和显式特征

除了结构节点标签之外，节点信息矩阵 X 还提供了包含潜在和显式特征的机会。通过将每个节点的嵌入属性向量连接到其在 X 中的相应行，我们观察到 GNN 可以通过仅拟合这部分信息来快速找出此类链接存在信息并进行优化。这导致我们的实验中泛化性能不佳。我们的技巧是将 $E_n$ 临时添加到 E 中, 即添加不存在的边。这样，正负训练链接将具有相同的链接存在信息记录在嵌入中，因此 GNN 无法仅通过拟合这部分信息来对链接进行分类。我们凭经验验证了这一技巧对 SEAL 的性能大大提高。我们将此技巧命名为负注入。

实验结果
Code : https://github.com/muhanzhang/SEAL/tree/master/Python

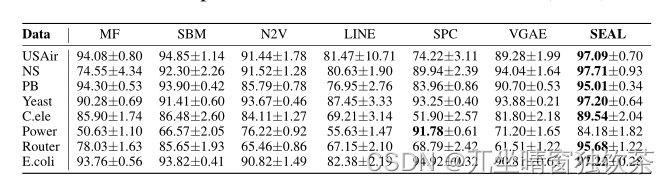
图1是与启发式方法的比较结果

图2是与潜在特征比较的结果

创作打卡挑战赛

赢取流量/现金/CSDN周边激励大奖