METHODS FOR NON-LINEAR LEAST SQUARES PROBLEMS(四)
3.3. Powell 的 Dog Leg方法
与列文伯格-马尔夸特方法一样,该方法使用高斯-牛顿法和最陡下降方向的组合。但是通过信赖域的半径显式控制两种方法之间的切换,参见第 2.4 节。 Powell 的名字与算法有关,因为他提出了如何找到由 (2.23) 定义的 h t r \pmb{h}_{tr} hhhtr? 的近似值。
给定
f
:
R
n
→
R
m
f: \mathbb{R}^n \to \mathbb{R}^m
f:Rn→Rm。在当前迭代点
x
\pmb{x}
xxx 处,高斯-牛顿步长
h
g
n
\pmb{h}_{gn}
hhhgn? 是如下线性系统的最小二乘解
J
(
x
)
h
≈
?
f
(
x
)
(3.17)
\pmb{J}(\pmb{x})\pmb{h} \approx -\pmb{f}(\pmb{x}) \tag{3.17}
JJJ(xxx)hhh≈?f?f??f(xxx)(3.17)
它可以通过求解下面的正规方程来计算
(
J
(
x
)
T
J
(
x
)
)
h
g
n
=
?
J
(
x
)
T
f
(
x
)
(3.18?a)
(\pmb{J}(\pmb{x})^T\pmb{J}(\pmb{x}))\pmb{h}_{gn} = -\pmb{J}(\pmb{x})^T\pmb{f}(\pmb{x}) \tag{3.18 a}
(JJJ(xxx)TJJJ(xxx))hhhgn?=?JJJ(xxx)Tf?f??f(xxx)(3.18?a)
最陡下降方向由下式给出
h
s
d
=
?
g
=
?
J
(
x
)
T
f
(
x
)
(3.18?b)
\pmb{h}_{sd} = -\pmb{g} = -\pmb{J}(\pmb{x})^T\pmb{f}(x) \tag{3.18 b}
hhhsd?=?g?g??g=?JJJ(xxx)Tf?f??f(x)(3.18?b)
这是一个方向,而不是步长,为了知道我们应该走多远,我们观察线性模型
f
(
x
+
α
h
s
d
)
≈
f
(
x
)
+
α
J
(
x
)
h
s
d
f(\pmb{x}+\alpha \pmb{h}_{sd}) \approx \pmb{f}(\pmb{x}) + \alpha \pmb{J}(\pmb{x}) \pmb{h}_{sd}
f(xxx+αhhhsd?)≈f?f??f(xxx)+αJJJ(xxx)hhhsd?
F ( x + α h s d ) = ≈ 1 2 ∣ ∣ f ( x ) + α J ( x ) h s d ∣ ∣ 2 = F ( x ) + α h s d T J ( x ) T f ( x ) + 1 2 α 2 ∣ ∣ J ( x ) h s d ∣ ∣ 2 F(\pmb{x}+\alpha \pmb{h}_{sd}) = \approx \frac{1}{2} ||\pmb{f}(\pmb{x}) + \alpha \pmb{J}(\pmb{x}) \pmb{h}_{sd}||^2 \\ =F(\pmb{x}) + \alpha \pmb{h}_{sd}^T \pmb{J}(\pmb{x})^T \pmb{f}(\pmb{x}) + \frac{1}{2}\alpha^2 ||\pmb{J}(\pmb{x})\pmb{h}_{sd}||^2 F(xxx+αhhhsd?)=≈21?∣∣f?f??f(xxx)+αJJJ(xxx)hhhsd?∣∣2=F(xxx)+αhhhsdT?JJJ(xxx)Tf?f??f(xxx)+21?α2∣∣JJJ(xxx)hhhsd?∣∣2
这个关于
α
\alpha
α 的函数的最小值为
α
=
?
h
s
d
T
J
(
x
)
T
f
(
x
)
∣
∣
J
(
x
)
h
s
d
∣
∣
2
=
∣
∣
g
∣
∣
2
∣
∣
J
(
x
)
g
∣
∣
2
(3.19)
\alpha = - \frac{\pmb{h}_{sd}^T \pmb{J}(\pmb{x}) ^T \pmb{f}(\pmb{x})}{||\pmb{J}(\pmb{x}) \pmb{h}_{sd}||^2} = \frac{||\pmb{g}||^2}{||\pmb{J}(\pmb{x})\pmb{g}||^2} \tag{3.19}
α=?∣∣JJJ(xxx)hhhsd?∣∣2hhhsdT?JJJ(xxx)Tf?f??f(xxx)?=∣∣JJJ(xxx)g?g??g∣∣2∣∣g?g??g∣∣2?(3.19)
现在我们从当前点 x \pmb{x} xxx 开始有两个候选步长: a = α h s d \pmb{a} = \alpha \pmb{h}_{sd} aaa=αhhhsd? 和 b = h g n \pmb{b} = \pmb{h}_{gn} bbb=hhhgn?。Powell 建议当信赖域半径为 Δ \Delta Δ 时使用以下策略来选择步长。
i f ∣ ∣ h g n ∣ ∣ ≤ Δ h d l : = h g n e l s e i f ∣ ∣ α h s d ∣ ∣ ≥ Δ h d l : = ( Δ ∣ ∣ h s d ∣ ∣ ) h s d e l s e h d l : = α h s d + β ( h g n ? α h s d ) (3.20?a) \quad \quad \quad \quad if \quad ||\pmb{h}_{gn}|| \leq \Delta \\ \quad \quad \quad \quad \pmb{h}_{dl}:= \pmb{h}_{gn} \\ \quad \quad \quad \quad \quad \quad elseif \quad ||\alpha \pmb{h}_{sd}|| \geq \Delta \\ \quad \quad \quad \quad \quad \quad \quad \pmb{h}_{dl}:=(\frac{\Delta}{||\pmb{h}_{sd}||})\pmb{h}_{sd} \\ else \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \pmb{h}_{dl}:= \alpha \pmb{h}_{sd} + \beta(\pmb{h}_{gn - \alpha \pmb{h}_{sd}}) \tag{3.20 a} if∣∣hhhgn?∣∣≤Δhhhdl?:=hhhgn?elseif∣∣αhhhsd?∣∣≥Δhhhdl?:=(∣∣hhhsd?∣∣Δ?)hhhsd?elsehhhdl?:=αhhhsd?+β(hhhgn?αhhhsd??)(3.20?a)
其中选择 β β β 的选择需要满足使 ∣ ∣ h d l ∣ ∣ = Δ ||\pmb{h}_{dl}|| = \Delta ∣∣hhhdl?∣∣=Δ 。
图 3.4 说明了策略中的最后一种情况。
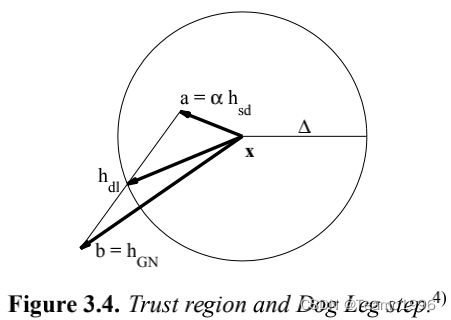
Dog Leg 的名称取自高尔夫:“Dog leg” 处的球道形状为从 x \pmb{x} xxx(开球点)通过 a \pmb{a} aaa 的终点到 h d l \pmb{h}_{dl} hhhdl? 的终点(球洞)的线。Powell 是一位热心的高尔夫球手!
使用上面定义的
a
\pmb{a}
aaa 和
b
\pmb{b}
bbb,并且
c
=
a
T
(
b
?
a
)
c = \pmb{a}^T(\pmb{b}-\pmb{a})
c=aaaT(bbb?aaa) 我们可以写出
ψ
(
β
)
=
∣
∣
a
+
β
(
b
?
a
)
∣
∣
2
?
Δ
2
=
∣
∣
b
?
a
∣
∣
2
β
2
+
2
c
β
+
∣
∣
a
2
∣
∣
?
Δ
2
\psi(\beta) = ||\pmb{a} + \beta(\pmb{b}-\pmb{a})||^2 - \Delta^2= ||\pmb{b}-\pmb{a}||^2\beta^2 + 2c\beta +||\pmb{a}^2|| - \Delta^2
ψ(β)=∣∣aaa+β(bbb?aaa)∣∣2?Δ2=∣∣bbb?aaa∣∣2β2+2cβ+∣∣aaa2∣∣?Δ2
我们为这个二阶多项式求根,并注意当 β → ? ∞ \beta \to - \infty β→?∞ 时 ψ → ∞ \psi \to \infty ψ→∞; ψ ( 0 ) = ∣ ∣ a ∣ ∣ 2 ? Δ 2 < 0 \psi(0) = ||\pmb{a}||^2 - \Delta^2 < 0 ψ(0)=∣∣aaa∣∣2?Δ2<0; ψ ( 1 ) = ∣ ∣ h g n ∣ ∣ 2 ? Δ 2 > 0 \psi(1) = ||\pmb{h}_{gn}||^2 - \Delta^2 > 0 ψ(1)=∣∣hhhgn?∣∣2?Δ2>0。因此, ψ \psi ψ 在 ] 0 , 1 [ ]0, 1[ ]0,1[ 中有一个负根和一个根。我们寻求后者,其最准确的计算值由下式给出
根据二次函数的形式 ] 0 , 1 [ ]0, 1[ ]0,1[ 应该表示 0 的左边和 0-1 之间,但这个表示方法确实没见过
i f c < 0 β = ( ? c + c 2 + ∣ ∣ b ? a ∣ ∣ 2 ( Δ 2 ? ∣ ∣ a ∣ ∣ 2 ) ) / ∣ ∣ b ? a ∣ ∣ 2 e l s e β = ( Δ 2 ? ∣ ∣ a ∣ ∣ 2 ) / ( c + c 2 + ∣ ∣ b ? a ∣ ∣ 2 ( Δ 2 ? ∣ ∣ a ∣ ∣ 2 ) ) (3.20?b) if \quad c<0 \\ \beta = (-c + \sqrt{c^2 + ||\pmb{b}-\pmb{a}|| ^2 (\Delta^2 - ||\pmb{a}||^2)}) / ||\pmb{b}-\pmb{a}||^2 \\ else \\ \beta = (\Delta ^2 - ||\pmb{a}||^2 )/ (c+ \sqrt{c^2 + ||\pmb{b}-\pmb{a}|| ^2 (\Delta^2 - ||\pmb{a}||^2)}) \tag{3.20 b} ifc<0β=(?c+c2+∣∣bbb?aaa∣∣2(Δ2?∣∣aaa∣∣2)?)/∣∣bbb?aaa∣∣2elseβ=(Δ2?∣∣aaa∣∣2)/(c+c2+∣∣bbb?aaa∣∣2(Δ2?∣∣aaa∣∣2)?)(3.20?b)
与 L-M 方法一样,我们可以使用增益比率
?
=
F
(
x
)
?
F
(
x
+
h
d
l
)
L
(
0
)
?
L
(
h
d
l
)
\wp = \frac{F(x) - F(x+h_{dl})}{L(0) - L(h_{dl})}
?=L(0)?L(hdl?)F(x)?F(x+hdl?)?
来控制迭代。同样,
L
L
L 是线性模型
L
(
h
)
=
1
2
∣
∣
f
(
x
)
+
J
(
x
)
h
∣
∣
2
L(\pmb{h}) = \frac{1}{2} ||\pmb{f}(\pmb{x}) + \pmb{J}(\pmb{x})\pmb{h}||^2
L(hhh)=21?∣∣f?f??f(xxx)+JJJ(xxx)hhh∣∣2
在 L-M 方法中,我们使用 ? \wp ? 来控制阻尼参数的大小。在这里,我们使用它来控制信赖域的半径 Δ \Delta Δ。较大的 ? \wp ? 值表示线性模型良好。我们可以增加 Δ \Delta Δ 从而使用更长的步长,它们将更接近高斯-牛顿方向。如果 ? \wp ? 很小(甚至可能是负数),那么我们会减小 Δ \Delta Δ,这意味着更小的步长,更接近最陡的下降方向。下面我们总结一下算法。

我们有以下说明。
- 初始化。 x 0 \pmb{x}_0 xxx0? 和 Δ 0 \Delta_0 Δ0? 应由用户提供。
- 我们使用补充了 ∣ ∣ f ( x ) ∣ ∣ ∞ ≤ ? 3 ||\pmb{f}(\pmb{x})||_{\infty} \leq \epsilon_3 ∣∣f?f??f(xxx)∣∣∞?≤?3? 的停止准则 (3.15),体现了 m = n m = n m=n 时 f ( x ? ) = 0 \pmb{f}(\pmb{x}^*) = 0 f?f??f(xxx?)=0 的情况,即非线性方程组的求解问题。
- 如果 m = n m = n m=n,那么 ≈ \approx ≈ 被 = = = 代替,参见(3.6),并且我们不使用正规方程(3.18a)对应的迂回策略;见例 3.9
- 对应于(3.20a)中的三种情况,我们可以证明
L ( 0 ) ? L ( h d l ) = { F ( x ) i f h d l = h g n Δ ( 2 ∣ ∣ α g ∣ ∣ ? Δ ) 2 α i f h d l = ? Δ ∣ ∣ g ∣ ∣ g 1 2 α ( 1 ? β ) 2 ∣ ∣ g ∣ ∣ 2 + β ( 2 ? β ) F ( x ) o t h e r w i s e L(\pmb{0}) - L(\pmb{h}_{dl}) = \begin{cases} F(\pmb{x}) \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad if \quad \pmb{h}_{dl} = \pmb{h}_{gn} \\ \frac{\Delta(2||\alpha \pmb{g}|| - \Delta)}{2 \alpha} \quad \quad \quad \quad \quad \quad \quad \quad if \quad \pmb{h}_{dl} = \frac{-\Delta}{||\pmb{g}||} \pmb{g} \\ \frac{1}{2} \alpha (1-\beta)^2 ||\pmb{g}||^2 + \beta(2-\beta) F(\pmb{x}) \quad otherwise\end{cases} L(000)?L(hhhdl?)=??????F(xxx)ifhhhdl?=hhhgn?2αΔ(2∣∣αg?g??g∣∣?Δ)?ifhhhdl?=∣∣g?g??g∣∣?Δ?g?g??g21?α(1?β)2∣∣g?g??g∣∣2+β(2?β)F(xxx)otherwise? - 策略(2.19)用于更新信赖域半径。
- 额外的停止标准。如果 Δ ≤ ? 2 ( ∣ ∣ x ∣ ∣ + ? 2 ) \Delta \leq \epsilon_2 (||\pmb{x}|| + \epsilon_2) Δ≤?2?(∣∣xxx∣∣+?2?),那么在下一步中肯定会满足(3.15b)。
示例 3.9.
在示例 3.6 中,我们简要讨论了步长 h l m \pmb{h}_{lm} hhhlm? 的计算并认为我们不妨通过正规方程(3.13)来计算它。假设 μ \mu μ 不是非常小,则矩阵的条件相当好,并且不会有舍入误差的过度影响。
Dog Leg 方法也适用于求解非线性方程组,即其中 (3.17) 是如下线性方程组的平方系统
J
(
x
)
h
=
?
f
(
x
)
\pmb{J}(\pmb{x})\pmb{h} = -\pmb{f}(\pmb{x})
JJJ(xxx)hhh=?f?f??f(xxx)
解 h = h n r \pmb{h} = \pmb{h}_{nr} hhh=hhhnr?,牛顿-拉夫森步长,参见示例 3.2。雅各比矩阵 J \pmb{J} JJJ 可能是病态的(甚至是奇异的),在这种情况下,如果我们使用(3.18a)计算 h g n \pmb{h}_{gn} hhhgn?,则舍入误差往往会主导解。
在 immoptibox 中的 dogleg 实现中,针对这些问题计算了 (3.17) 的解。如果 J ( x ) \pmb{J}(\pmb{x}) JJJ(xxx) 的列不是显著线性独立的,则最小二乘解 h \pmb{h} hhh 不是唯一的,并且 h g n \pmb{h}_{gn} hhhgn? 为具有最小范数的 h \pmb{h} hhh。该计算的一些细节在附录 B 中给出。
示例 3.10.
图 3.5 说明了Dog Leg方法应用于示例 3.2 和 3.8 中的 Powell 问题的性能,起点 x 0 = [ 3 , 1 ] T \pmb{x}_0 = [3, 1]^T xxx0?=[3,1]T, Δ 0 = 1 \Delta_0 = 1 Δ0?=1,停止标准由 ? 1 = ? 2 = 1 0 ? 15 \epsilon_1 = \epsilon_2 = 10^{?15} ?1?=?2?=10?15, ? 3 = 1 0 ? 20 \epsilon_3= 10^{?20} ?3?=10?20, k m a x = 100 k_{max} = 100 kmax?=100 给出。
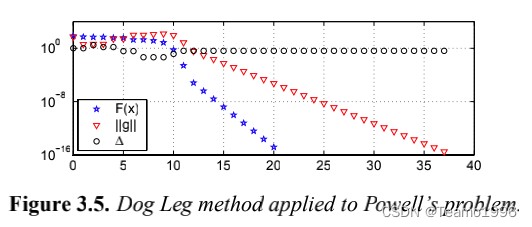
由于梯度很小,迭代在 37 步后停止,返回 x = [ ? 2.41 ? 1 0 ? 35 , 1.26 ? 1 0 ? 9 ] T \pmb{x} = [ ?2.41\cdot 10^{?35}, 1.26\cdot 10^{?9} ]^T xxx=[?2.41?10?35,1.26?10?9]T,这是 x ? = 0 \pmb{x}^? = 0 xxx?=0 的一个很好的近似值。如图 3.5 所示最终收敛是线性的(由 J ( x ? ) \pmb{J}(\pmb{x}^*) JJJ(xxx?) 的奇异性引起),但比马尔夸特方法快得多。
示例 3.11.
我们在示例 1.1、3.4 和 3.7 中的数据拟合问题上使用了算法 3.21。与示例 3.7 一样,我们使用起点 x 0 = [ ? 1 , ? 2 , 1 , ? 1 ] T \pmb{x}_0 = [-1, -2, 1, -1]^T xxx0?=[?1,?2,1,?1]T,并取 Δ 0 = 1 \Delta_0 = 1 Δ0?=1 和 ? 1 = ? 2 = ? 3 = 1 0 ? 8 \epsilon_1 = \epsilon_2 = \epsilon_3 = 10^{-8} ?1?=?2?=?3?=10?8, k m a x = 200 k_{max} = 200 kmax?=200 给出的停止迭代标准。 算法在 x ≈ [ ? 4 , ? 5 , 4 , ? 4 ] T \pmb{x}\approx [?4, ?5, 4, ?4]^T xxx≈[?4,?5,4,?4]T 对应的的 30 次迭代步骤后停止。性能如下图所示。如图 3.6 所示,我们注意到最终收敛速度非常快。
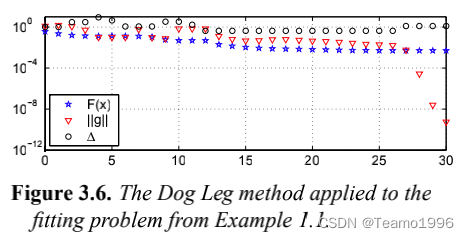
最后两个例子似乎表明 Dog Leg 方法明显优于列文伯格-马尔夸特方法。当最小二乘问题由非线性方程组产生时,这是正确的。 Dog Leg 方法目前被认为是求解非线性方程组的最佳方法。
对于通用最小二乘问题,Dog Leg 方法与 L-M 方法具有相同的缺点:如果 F ( x ? ) ≠ 0 F(\pmb{x}^*) \neq 0 F(xxx?)?=0,则最终收敛可以预期是线性的(并且缓慢的)。对于给定的问题和给定的初始猜测 x 0 \pmb{x}_0 xxx0? 无法事先说这两种方法中的哪一种会更快。
